A Reasonable Approximation
Latest posts
PD-alikes in two dimensions
Some time after writing Classifying games like the prisoner's dilemma, I read a paper (I forget which) which pointed out that these games can be specified with just two numbers.
Recall that they have the following payoff matrix:
| Player 2 | |||
|---|---|---|---|
| Krump | Flitz | ||
| Player 1 | Krump | $(W, W)$ | $(X, Y)$ |
| Flitz | $(Y, X)$ | $(Z, Z)$ |
where $W > Z$.1 We can apply a positive affine transformation (that is, $n ↦ an + b$ where $a > 0$) to all of $W, X, Y, Z$ without changing the game. So let's pick the function $n ↦ {n - Z \over W - Z}$. This sends $W$ to $1$ and $Z$ to $0$, leaving us with just two parameters: $R = {X - Z \over W - Z}$ and $S = {Y - Z \over W - Z}$.
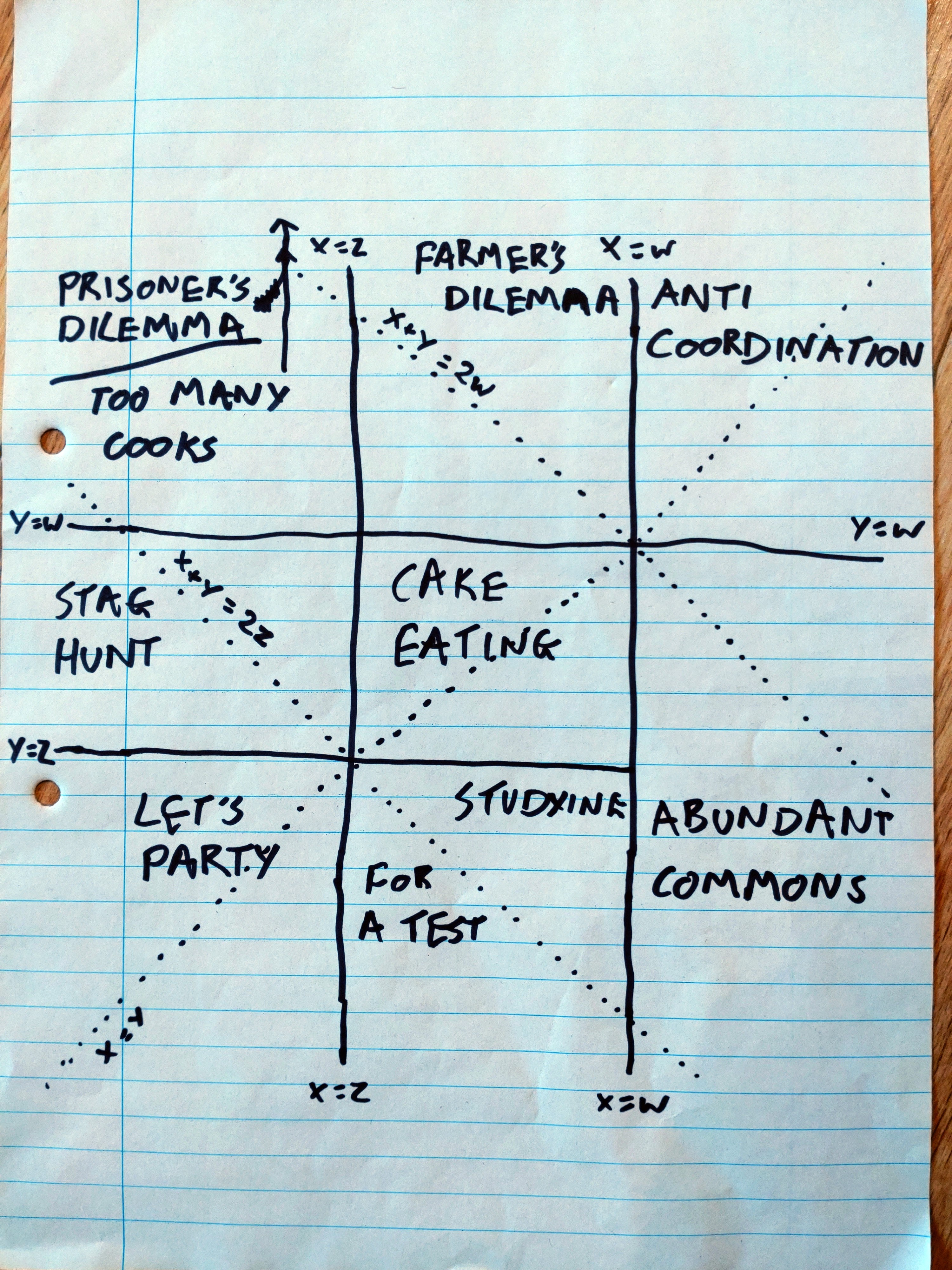
So what happens if we plot the space of these games on a graph? The lines $ \{X, Y\} = \{W, Z\} $ become $ \{R, S\} = \{0, 1\} $, i.e. vertical and horizontal lines. The lines $X + Y = 2W$ and $X + Y = 2Z$ become the diagonals $R + S = 2$ and $R + S = 0$; and $X = Y$ becomes the diagonal $R = S$. Drawing those lines, and relabelling in terms of $W, X, Y, Z$, it looks like this:
Note that Cake Eating (my favorite game) is the only one with a finite boundary; the other boxes extend to infinity. There are also finite components in the Farmer's Dilemma (with $X + Y < 2W$), and Stag Hunt and Studying For a Test (with $X + Y > 2Z$). As drawn, Prisoner's Dilemma occupies almost all of the box it shares with Too Many Cooks; but Too Many Cooks (above the line $X + Y = 2W$) is also infinite. (I initially got those the wrong way around, so the drawing isn't very clear there.)
I don't know if we learn much from this, but here it is.
-
In the previous post I mostly ignored equalities because it was mildly convenient to do so. But the analysis here completely fails if we allow $W=Z$. So now I'm ignoring them because it's considerably more convenient to do so. ↩
Posted on 03 April 2022
Tagged: game theory; math
Comments elsewhere: LessWrong