I'm a big fan of the game Zendo. But I don't think it suits large groups very well. The more other players there are, the more time you spend sitting around; and you may well get only one turn. I also think a game tends to take longer with more players.
Here's an alternate ruleset you can use if you have a large group. I think I've played it 2-3 times, with 15-ish? players, and it's finished in about 30 minutes each time, including explaining the rules to people who'd never played Zendo before.
For people who know the typical rules, here's the diff from them:
-
After the initial two samples are given, players run experiments in real time, whenever they feel like they have one they want to run, and the universe marks them. There's no turn taking, and no need to wait for one player to finish their experiment before you start constructing yours. Just try to make it clear when you have finished.
-
At any time, a player can guess the rule. They announce clearly that they want to guess, and then play pauses until they're done. If they take too long, the universe should probably set a time limit, but I don't think this has been a problem.
-
If they guess correctly, they win. If not, they can no longer guess. The universe provides a counterexample, and play resumes.
-
I've never run out of players before someone guesses the rule. Two options would be "everyone gets their guess back" and "game over".
Another change (starting from the standard rules) that I think might speed games up, is the ability to spend multiple funding tokens to publish a paper out of turn. But I've only run this once, needing three tokens, and no one took advantage of it. Maybe I'll try with two at some point.
Posted on 23 September 2025
|
Comments
I've previously complained about how people often repeat a quote that starts with
The reason that the rich were so rich, Vimes reasoned, was because they managed to spend less money.
(Terry Pratchett, Men at Arms)
…and then don't seem to realize that the thing they're quoting is saying "rich people spend less money than poor people, and that's why they're rich". It seems to me that people interpret it as saying various different things, but rarely the thing it's quite obviously saying.
Here's an oversight in my previous complaint: I didn't look at Wikipedia. I picked up vibes from a few internet randos, but not the specific internet randos who edit the world's premier encyclopedia.
Part of what I want to point out here is "there's no consensus on what the term boots theory refers to". If I'm wrong about that, and just happened to read the wrong internet randos, it seems likely that Wikipedia will tell me what the consensus is. So let's take a look.
As I write, the most recent revision is from March 17 2025, and it tells us:
The Sam Vimes theory of socioeconomic unfairness, often called simply the boots theory, is an economic theory that people in poverty have to buy cheap and subpar products that need to be replaced repeatedly, proving more expensive in the long run than more expensive items.
Come to think of it, this is actually a stronger claim than what I called level 1 boots theory. I described that as "being rich enables you to spend less money on things", but this is a specific way that being rich enables you to spend less money on things. Maybe it is worth having a term for this distinct from "ghetto tax", which is what I suggested previously. (But that term shouldn't necessarily be "boots theory".)
So that's what Wikipedia says "boots theory" refers to. Let's follow its citations and see why Wikipedia says that.
Wikipedia:
In the Discworld series of novels by Terry Pratchett, Sam Vimes is the captain of the City Watch of the fictional city-state of Ankh-Morpork.[1][2]
This doesn't talk about boots theory at all, but following the citations anyway:
[1] is The Guardian, Terry Pratchett estate backs Jack Monroe's idea for 'Vimes Boots' poverty index. This is an article about someone named Jack Monroe creating a price index, intended as an alternative to CPI, and naming it the "Vimes Boots Index".
As a source for Wikipedia's claim, the relevant part of this is quoting Rhianna Pratchett, who says:
My father used his anger about inequality, classism, xenophobia and bigotry to help power the moral core of his work. One of his most famous lightning-rods for this was Commander Vimes of the Ankh-Morpork City Watch
I note pedantically that Commander is a different rank than Captain. (Vimes is promoted from Captain to Commander in Men at Arms.)
On the subject of boots theory, we have the original quote from Men at Arms, starting (as usual) with "the reason that the rich were so rich". Rihanna calls it a "musing on how expensive it is to be poor via the cost of boots".
We're not told how the index is calculated or how it relates to boots theory except that it's "named in honour" of it.
(Incidentally, Monroe's own Wikipedia page doesn't mention the Vimes Boots Index at all.)
[2] is an NYT financial advice column, I think? Spend the Money for the Good Boots, and Wear Them Forever. It mostly boils down to someone giving an example where buying an expensive thing now saved money in the long run compared to buying cheap things. He bought \$300 ski pants that have lasted 17 years and counting, and claims that if he'd bought \$50 ski pants instead, he'd have had to buy a new pair every year, spending over \$800.
Note, there's an important calculation that he skips. If he'd invested \$300 in the S&P 500 in 1999, this site claims it would have been worth \$762 nominal in 2016, or \$528 inflation-adjusted. So yes, if he has the numbers right, it seems like this was probably a good financial investment on his part.
Anyway. This article does back the cited claim (albeit without using the phrase "City Watch"). On the subject of boots theory, it includes the original quote (starting, as usual, with "the reason that the rich were so rich") and doesn't take it any further than "you can spend more money now to spend less money in total". The example it gives matches Wikipedia's definition of boots theory.
Back to Wikipedia:
In the 1993 novel Men at Arms, the second novel focusing on the City Watch through Vimes' perspective, Vimes muses on how expensive it is to be poor:[2][3]
We just discussed [2]. [3] is Gizmodo, Discworld's Famous 'Boots Theory' Is Putting a Spotlight on Poverty in the UK. This is another announcement of the Vimes Boots Index. It gives a little more detail on how it relates to boots theory:
Monroe drew parallels to the famous passage's explanation to how low-income families in the UK have seen supermarkets either noticeably increase prices on "budget" lines of basic food and goods (an example Monroe used cited an over 300% increase on a bag of rice at one store in the last year, while cutting the amount of rice in the bag in half) as the country faces the continuing economic effects of Brexit, the covid-19 pandemic, and general supply chain issues. With these lines, aimed at low-income households, either pricing up or being replaced with more expensive store-brand ranges, struggling families are being forced to turn to charities and food banks to sustain themselves, reckoning with over a decade of cuts to social support programs by Britain's series of Conservative governments, including Boris Johnson's current cabinet, itself rather busy right now trying to hide a long string of embarrassing, potentially illegal social gatherings by the Prime Minister during covid-19 lockdowns.
…except that I don't see much connection. But boy, impressive segue in that second sentence.
Wikipedia now gives the original quote, starting as usual with "the reason that the rich were so rich". This is citation 4, pointing at Men at Arms. Then:
In the New Statesman, Marc Burrows hypothesized Pratchett drew inspiration from Robert Tressell's 1914 novel The Ragged-Trousered Philanthropists.[5]
[5] is the New Statesman, Your best ally against injustice? Terry Pratchett. This is another piece talking about the Vimes Boots Index. It gives an extra hint about how it's calculated:
[Monroe has] been monitoring the true "cost of living" for over a decade – not the one the ONS espouses, based on the price of 700 pre-selected goods including (as Monroe wryly notes in their article in the Observer) "a leg of lamb, bedroom furniture, a television and champagne", but the ones familiar to those who have no choice but to spend the absolute minimum: value ranges, budget items and absolute basics. The ONS bases its statistics on average prices, but for millions of the country’s poorest, average prices don’t reflect reality at all.
On the subject of boots theory, we get the original quote, refreshingly not starting with "the reason that the rich were so rich" - it starts with "take boots, for example". As commentary, it says "being poor is actually more expensive than being wealthy".
(That sounds a lot like "poor people spend more money than rich people", but they're not quite the same. If I say "owning an Aston Martin is more expensive than owning a Ford", you probably assume that the cost of driving, maintaining and insuring a Martin in some minimal adequate condition is higher than doing that for a Ford. But some people will voluntarily spend more than the minimum, and some Ford owners will spend more on their cars than some Martin owners; and Ford owners may well spend more than Martin owners on non-car stuff. So it would be coherent to say something like: "being poor is more expensive than being rich, in the sense that poor people are forced to spend more money on daily living activities. But rich people typically spend more than they're forced to, and more than poor people overall, on daily living activities and other stuff." I'm not sure if I've previously realized this distinction.)
Wikipedia:
In the book Fashion in the Fairy Tale Tradition, Rebecca-Anne C. Do Rozario argued "shoes and economic autonomy are inexorably linked" in fairy tales, citing the Boots theory as "particularly relevant" and "an insightful metaphor for inequality".[6]
[6] is just a link to page 180 of that book. It doesn't have much more than what Wikipedia gives:
Shoes and economic autonomy are inexorably linked. Terry Pratchett, with his firm understanding of how fairy tales operate, places the "'Boots' theory of socio-economic unfairness" in the mind of Sam Vimes in Men at Arms (1993). It is an insightful metaphor for inequality articulated through shoe-wear: "A man who could afford fifty dollars had a pair of boots that'd still be keeping his feet dry in ten years' time, while a poor man who could only afford cheap boots would have spent a hundred dollars on boots in the same time and would still have wet feet."
This might be the shortest extract of the quote I've seen yet.
("Particularly relevant" seems to come from a footnote on page 213. I can locate it through search but there's no preview available for the page.)
Wikipedia:
In 2013, an article by the US ConsumerAffairs made reference to the theory in regard to purchasing items on credit, specifically regarding children's boots from the retailer Fingerhut; a \$25 pair of boots, at the interest rates being offered, would cost \$37 if purchased over seven months.[7]
This seems to switch the idea from "in the long run, repeatedly buying cheap things costs more than buying expensive things" to "buying things with money you don't hand over yet costs more than buying things with money you hand over immediately". Or, "people won't typically lend you money for free".
The article (ConsumerAffairs, Fingerhut boots and the Vimes' Boots paradox) even notices this leap. ("though we haven't tested this ourselves, we're sure that Carrini boots or Reebok sneakers bought from Fingerhut are just as good as Carrini or Reebok items bought elsewhere.)
We're given the original quote, starting as usual with "the reason that the rich were so rich".
Wikipedia:
In 2016, the left-wing blog Dorset Eye also ran an article discussing the theory, giving fuel poverty in the United Kingdom as an example of its application, citing a 2014 Office for National Statistics (ONS) report that those who pre-paid for electricity—who were most likely to be subject to fuel poverty—paid 8% more on their electricity bills than those who paid by direct debit.[8]
Dorset Eye, Mike Deverell discusses five reasons why those with less end up paying more.
Welp, uh, this is kind of a case where people will lend you money for free, if you have money. It fits a broad "being poor is expensive" narrative, but it's not a case where rich people buy a more expensive thing up front to save money in the long run.
Other than fuel poverty, the article gives four more reasons "why it's so difficult to climb out of the poverty trap": VAT, other taxes, food poverty and austerity. None seem to have any relation to boots theory. The article doesn't explicitly say they're examples of it, and Wikipedia doesn't mention them, so I'll leave them out.
We get the original quote, starting with "the reason that the rich were so rich".
Wikipedia:
In a 2020 discussion paper for the Social and Political Research Foundation, Sitara Srinivas used the theory to analyze how sustainable fashion is inaccessible compared to fast fashion.[9]
Stitching a new narrative: engaging with sustainability in the fashion industry. The relevant part is:
Because of the higher pay to workers and quality of materials used, sustainable fashion usually is more expensive. As previously stated, a fast fashion brand white t-shirt costs on average Rs 824. A sustainably produced t-shirt on the other hand costs on average Rs 4825[4]. For the average working or middle class consumer, who may not have the money to invest in a piece of quality clothing that will last long, but also at the same time has the aspiration to dress fashionably, sustainable fashion then becomes an unachievable goal.
The 'Boots theory of socio-economic unfairness' engages with this phenomenon. Derived from a paragraph in Terry Pratchett's novel Men at Arms, it explores the idea that quality costs more in the short term, with a purchase being more expensive at first, and the cost per use reducing over time. For someone that cannot afford a quality piece of clothing, cheap clothing becomes the best option. While clothing that is made sustainably may last longer, fast fashion remains cheaper and hence more accessible (Ellen MacArthur Foundation).
Followed by the original quote, starting as usual with "the reason that the rich were so rich".
So this broadly matches Wikipedia's description of the term. It doesn't come right out and say "buying the expensive t-shirt is cheaper in the long run". But it's at least hinting in that direction.
Wikipedia:
In an article titled "The Price of Poverty" published in Tribune Magazine in 2022, the theory was cited as explaining the economic predicament in the United Kingdom. Examples provided included the higher cost of renting compared to home ownership, higher interest rates for loans to impoverished people, the effects of food poverty on educational advancement, and healthcare costs.[10]
Tribune, The Price of Poverty. This one doesn't give the original quote at all, describing boots theory in its own words:
This obvious injustice—subsidies for businesses, cost hikes for workers—is only one example of the reality spread across our economic system: that being in poverty is much more expensive than being rich.
Vimes' 'Boots Theory of Socio-Economic Unfairness'
To understand why poverty is so expensive, we can look to Samuel Vimes, Captain of the City Watch and protagonist of Terry Pratchett's Discworld novel Men at Arms. Vimes uses his 'Boots theory of socio-economic unfairness' to outline how the nobility of his city, Ankh-Morpork, could live twice as comfortably as him while spending half the money.
Vimes earned 38 dollars per month as captain of the watch. A really good pair of boots, the kind that would last for around 10 years, would cost around 50 dollars—far more than his monthly salary. As a result, he would have to buy the cheaper, lower-quality boots for 10 dollars, which would last for one year at most. Over a 10-year period, Vimes would spend 100 dollars on 10 pairs of boots (and would still have wet feet), whereas the noble would have only spent 50 dollars on one pair of boots during the same period.
(I repeat that Vimes is wrong about the nobility - at minimum, about the specific nobility he's thinking of, who is the richest woman in the city and his fiancée - spending less money than him.)
Here are the examples the article gives:
subsidies for businesses, cost hikes for workers
Roughly speaking, I think the idea here is "rich people's cost of living is going down and poor people's is going up". But that's talking about acceleration, not velocity.
Housing costs for private tenants have jumped by nearly 50% above the general rate of inflation in the last 25 years. House prices have also soared, but home ownership remains, often, the cheaper option.
So this is "spending more money up front is cheaper in the long term". You can even kind of make it fit the original definition: when you rent, you repeatedly purchase "the right to live in this place for the next month", but when you buy, you purchase that right once and keep it indefinitely. And the rights you purchase when you rent are typically worse than the rights you purchase when you buy (e.g. more restrictive about pets, or decoration, or interior layout).
(Note: costs of home ownership here do take into account "interest lost by paying a deposit rather than saving.")
Borrowing costs are also much higher for poor people because they are seen by lenders as higher risk, meaning they pay more interest on debt like overdrafts and credit cards.
"Poor people get less favorable terms when borrowing money."
In 2021, a study by the Food Foundation found that the poorest fifth of British society would need to spend 40% of their income to reach the government’s healthy eating guidelines. The chronic malnutrition caused by poverty has long-term costs, both to individuals and to society as a whole.
"Poor people don't get enough food, and that causes them long term problems."
A 2016 study by the Joseph Rowntree Foundation found that healthcare spending accounted for the largest portion of additional spending associated with poverty, at £29 billion. … The British Medical Journal has warned that unless the government acts to address the Cost of Living crisis, poverty, and therefore health inequalities and the costs associated with treating and managing them, will increase.
"Poor people are less healthy, and more expensive for the government to provide healthcare to."
Remember that Wikipedia's definition is
The Sam Vimes theory of socioeconomic unfairness, often called simply the boots theory, is an economic theory that people in poverty have to buy cheap and subpar products that need to be replaced repeatedly, proving more expensive in the long run than more expensive items.
Of the citations, it seems like three back this up? One with an example about ski pants, one with an example about t-shirts, and one talking about home ownership versus renting.
Other than those, here are some things that citations relate to boots theory:
- You can spend more money now to spend less money in total. (More general than Wikipedia's definition.)
- Being poor is more expensive than being rich. (More general again.)
- Buying things with money you don't hand over yet costs more than buying things with money you hand over immediately.
- Except that sometimes it costs less.
- Poor people get less favorable terms when borrowing money.
- Costs of living are going down for rich people and up for poor people.
- Poor people don't get enough food, and that causes them long term problems.
- Poor people are less healthy, and more expensive for the government to provide healthcare to.
…and for some of these, Wikipedia even includes them inline. You don't need to click through to the citations to realize that multiple different concepts are getting confused.
(Someone in the talk page has noticed the same thing: "The instances listed here aren't really examples of the same mechanism.")
(Also, when I wrote the previous essays, multiple commentators told me what they take boots theory to mean, but none of them picked Wikipedia's definition of it.)
So I think I'm vindicated in my complaints. Wikipedia's definition of "boots theory" is not consensus, even among Wikipedia's sources. There is no consensus.
Posted on 01 August 2025
|
Comments
I previously wrote about Boots theory, the idea that "the rich are so rich because they spend less money". My one-sentence take is: I'm pretty sure rich people spend more money than poor people, and an observation can't be explained by a falsehood.
The popular explanation of the theory comes from Sam Vimes, a resident of Ankh-Morpork on the Discworld (which is carried on the backs of four elephants, who themselves stand on a giant turtle swimming through space). I claim that Sam Vimes doesn't have a solid understanding of 21st Century Earth Anglosphere economics, but we can hardly hold that against him. Maybe he understands Ankh-Morpork economics?
To be clear, this is beside the point of my previous essay. I was talking about 21st Century Earth Anglosphere because that's what I know; and whenever I see someone bring up boots theory, they're talking about Earth (usually 21st Century Anglosphere) and not Ankh-Morpork. But multiple commentors brought it up.
Radmonger:
you need to understand Vimes as making a distinction not between the upper class and everyone else, but the middle class and the working class, between homeowners and renters.
This is completely wrong.
Ericf:
Vimes is thinking of the landed gentry when he is considering the "rich" - that would be the top 1%, not the tippy-top super-rich. Also, in a pseudo-medivial environment, the lifestyle inequality isn't as extreme as today's 50th % vs 1%.
This is closer, but still wrong.
WTFwhatthehell:
The quote in the book is about old money families vs the poor.
JC O:
It should be noted that Vimes was specifically thinking of real generational wealth in that area. He'd spent some time in the home of a Lady from oldest and wealthiest family in the city, and saw that everything was old there, solid, built to last forever. Generations of clothing tailored to the fit of the family members, and saved if it was still in good condition, and if it was not, the fabric would be reused to make something else. Even the garden tools were old. The family owned multiple homes in various cities and in the country, and they owned sizable portions of the real estate in the city.
These are basically right. (I'm not sure about all of JC O's specific details, and I'd strike "vs the poor".) Here's the extended quote (from Men at Arms):
She was, Vimes had been told, the richest woman in Ankh-Morpork. In fact she was richer than all the other women in Ankh-Morpork rolled, if that were possible, into one.
It was going to be a strange wedding, people said. Vimes treated his social superiors with barely concealed distaste, because the women made his head ache and the men made his fists itch. And Sybil Ramkin was the last survivor of one of the oldest families in Ankh. But they'd been thrown together like twigs in a whirlpool, and had yielded to the inevitable …
When he was a little boy, Sam Vimes had thought that the very rich ate off gold plates and lived in marble houses.
He'd learned something new: the very very rich could afford to be poor. Sybil Ramkin lived in the kind of poverty that was only available to the very rich, a poverty approached from the other side. Women who were merely well-off saved up and bought dresses made of silk edged with lace and pearls, but Lady Ramkin was so rich she could afford to stomp around the place in rubber boots and a tweed skirt that had belonged to her mother. She was so rich she could afford to live on biscuits and cheese sandwiches. She was so rich she lived in three rooms in a thirty-four-roomed mansion; the rest of them were full of very expensive and very old furniture, covered in dust sheets.
The reason that the rich were so rich, Vimes reasoned, was because they managed to spend less money.
Take boots, for example. He earned thirty-eight dollars a month plus allowances. A really good pair of leather boots cost fifty dollars. But an affordable pair of boots, which were sort of okay for a season or two and then leaked like hell when the cardboard gave out, cost about ten dollars. Those were the kind of boots Vimes always bought, and wore until the soles were so thin that he could tell where he was in Ankh-Morpork on a foggy night by the feel of the cobbles.
But the thing was that good boots lasted for years and years. A man who could afford fifty dollars had a pair of boots that'd still be keeping his feet dry in ten years' time, while a poor man who could only afford cheap boots would have spent a hundred dollars on boots in the same time and would still have wet feet.
This was the Captain Samuel Vimes 'Boots' theory of socio-economic unfairness.
The point was that Sybil Ramkin hardly ever had to buy anything. The mansion was full of this big, solid furniture, bought by her ancestors. It never wore out. She had whole boxes full of jewellery which just seemed to have accumulated over the centuries. Vimes had seen a wine cellar that a regiment of speleologists could get so happily drunk in that they wouldn't mind that they'd got lost without trace.
Lady Sybil Ramkin lived quite comfortably from day to day by spending, Vimes estimated, about half as much as he did. But she spent a lot more on dragons.
So Vimes is specifically distinguishing between the tippy-top super-rich and the "merely well-off".
There's, um, a lot to unpack here. It's kind of fractally wrong.
Note that bits of this don't make sense when taken literally. "Lady Ramkin was so rich she could afford to stomp around the place in rubber boots and a tweed skirt that had belonged to her mother. She was so rich she could afford to live on biscuits and cheese sandwiches." These are not expensive things compared to the alternatives.
I think the subtext here is something like "Lady Ramkin is so rich she doesn't need to try to impress people". Looking back at Guards! Guards! (the first book featuring Vimes and Ramkin), that's spelled out more explicitly: "A couple of women were moving purposefully among the boxes. Ladies, rather. They were far too untidy to be mere women. No ordinary women would have dreamed of looking so scruffy; you needed the complete self-confidence that comes with knowing who your great-great-great-great-grandfather was before you could wear clothes like that."
I'm tempted to attribute this to personality (speculatively, "autism") rather than wealth. But I think it does rhyme with discussions of class that I've seen. (Roughly: rich people don't want you to mistake them for middle-class, so they visibly spend money. The people richer than them aren't in danger of being mistaken for middle-class, but they don't want you to think they're merely "rich", so they avoid visibly spending money.) Let's stipulate that the subtext is accurate, and move on.
The mention of wine is out of place. Rich people don't have access to durable wine that isn't depleted when drunk. If Sybil Ramkin has a lot of wine, it's not because someone made a relatively small up-front investment in wine and now there's no need to buy wine ever again. It's because someone spent a lot of money to buy a lot of wine, and it just hasn't all been drunk yet.
Next, note the contradiction here:
- Sybil Ramkin is rich because she doesn't spend much money;
- Sybil Ramkin doesn't spend much money except on dragons.
She does spend a lot of money! She spends it on dragons! So that can't be why she's rich! An observation can't be explained by a falsehood.
Could it be true, if it weren't for the dragons?
("It's wet here. Might that be from the sprinkler?" "There is no sprinkler, so no." "Okay. But if there were a sprinkler, might that be why it's wet?")
No: I'm pretty sure "Sybil Ramkin doesn't spend much money on things other than dragons" is also false. Here are some snippets from Guards! Guards!:
Vimes had completely forgotten the Watch House. "It must have been badly damaged," he ventured.
"Totally destroyed," said Lady Ramkin. "Just a patch of melted rock. So I'm letting you have a place in Pseudopolis Yard."
"Sorry?"
"Oh, my father had property all over the city," she said. "Quite useless to me, really. So I told my agent to give Sergeant Colon the keys to the old house in Pseudopolis Yard. It'll do it good to be aired."
Lady Ramkin's coach rattled into the plaza making a noise like a roulette wheel and pounded straight for Vimes, stopping in a skid that sent it juddering around in a semi-circle and forced the horses either to face the other way or plait their legs.
An effort had been made to spruce up the Ramkin mansion, he noticed. The encroaching shrubbery had been pitilessly hacked back. An elderly workman atop a ladder was nailing the stucco back on the walls while another, with a spade, was rather arbitrarily defining the line where the lawn ended and the old flower beds had begun.
To his amazement the door was eventually opened by a butler so elderly that he might have been resurrected by the knocking.
A terrible premonition took hold of Vimes at the same moment as a gust of Captivation, the most expensive perfume available anywhere in Ankh-Morpork blew past him.
Vimes was vaguely aware of a brilliant blue dress that sparkled in the candlelight, a mass of hair the colour of chestnuts, a slightly anxious face that suggested that a whole battalion of skilled painters and decorators had only just dismantled their scaffolding and gone home, and a faint creaking that said underneath it all mere corsetry was being subjected to the kind of tensions more usually found in the heart of large stars.
He must have eaten, because servants appeared out of nowhere with things stuffed with other things, and came back later and took the plates away. The butler reanimated occasionally to fill glass after glass with strange wines. The heat from the candles was enough to cook by.
Ignore that she gives away a building: that's a one-off. Stipulate that all those servants and the expensive make-up and perfume are just another one-off to seduce Vimes: that's at least partly supported in the text, she normally does her own cooking. Ignore for some reason the two workmen. Pretend that her clothes and furniture and property need no upkeep at all - including the fancy-rather-than-practical clothes she sometimes wears throughout the book. Assume she drives the coach herself: it's a little weird that that's not mentioned, but there's no explicit mention of a driver either.
Even granting all that, she still needs to feed at least two horses! Horses, I am led to believe, are expensive. (And need a certain amount of time and attention, and do you think Sybil Ramkin spends her time taking care of horses when there are dragons to take care of?)
Do we further assume she just rents the horses every time she needs to use her coach? She walks, herself, down to someone else's stables. Then brings two horses back to her house, where she hooks them up to her coach. (Could she keep the coach at the stables? Not for free.) She drives her coach around herself, and when her business is concluded, she drops the coach back at her house, returns the horses, and walks home.
And why does she do this? If she was struggling, she might do it to save money. But she's not. She has property worth about seven million dollars a year.
I'm not willing to credit that she does this. But even if I was, how much does it cost to rent two horses for a few hours? It can't be cheap, and she does that multiple times in the book.
Plus, even when she's not explicitly trying to seduce him, she feeds Vimes bacon, fried potatoes, eggs, cake and bread pudding. Does Vimes get to eat these things often? ("Vimes thought about the meals at his lodgings. Somehow the meat was always gray, with mysterious tubes in it.")
This is not a person who lives on less money than Sam Vimes, and it's hard to believe Sam Vimes - a policeman, someone for whom "noticing things" is part of the job description, who is engaged to this woman - is ignorant of the fact.
That's based on Guards! Guards! What if we completely ignore that book, and just look at Men at Arms?
Then he dried himself off as best he could and looked at the suit on the bed.
It had been made for him by the finest tailor in the city. Sybil Ramkin had a generous heart. She was a woman out for all she could give.
The suit was blue and deep purple, with lace on the wrists and at the throat. It was the height of fashion, he had been told.
Willikins had also laid out a dressing gown with brocade on the sleeves. He put it on, and wandered into his dressing room.
That was another new thing. The rich even had rooms for dressing in, and clothes to wear while you went into the dressing rooms to get dressed.
(Hardly "rubber boots and a tweed skirt that had belonged to her mother", or "three rooms in a thirty-four-roomed mansion".)
"His lordship … that is, her ladyship's father … he required to have his back scrubbed," said Willikins.
(i.e. the butler seems to be a regular fixture.)
And this wasn't one of the old hip bath, drag-it-in-front-of-the-fire jobs, no. The Ramkin mansion collected water off the roof into a big cistern, after straining out the pigeons, and then it was heated by an ancient geyser [footnote: "Who stoked the boiler."]
(i.e. that's another person who needs to be paid.)
Lady Sybil was devoting to her wedding all the directness of thought she'd normally apply to breeding out a tendency towards floppy ears in swamp dragons. Half a dozen cooks had been busy in the kitchens for three days. They were roasting a whole ox and doing amazing stuff with rare fruit.
(Sybil Ramkin is so rich she can afford to live on biscuits and cheese sandwiches. But sometimes she likes to slum it, and spend money as if she was merely well-off.)
Also, I didn't find a convenient quote for this, but she hosts a dinner for a bunch of other rich people and somehow I doubt she asks them to pay for it.
I can offer two defenses of Vimes here. One is that all of this is from from after the quote about boots theory, so - again, as long as we're pretending Guards! Guards! never happened - maybe he didn't know all this at the time, and then he'd still be embarrassingly wrong but a bit less embarrassingly wrong. Like, he'd be making up shit that defies common sense, and it's weird he knows so little about his fiancée, but he wouldn't be making up shit that contradicts what he's seen himself.
The stronger one is that it's revealed he gives away \$14/month to the widows and orphans of coppers. That increases the apparent spending power of his \$38/month. So when he thinks Sybil spends less than he does, she has more margin to do that in.
But still. C'mon.
Might Vimes have been right in general, but wrong about Sybil Ramkin?
I don't think we see much else of the very very rich. We're told Vimes doesn't either. (Men at Arms: "He hadn't had much experience with the rich and powerful.") If there's any reason for Vimes to think "the rich spend less money than the poor" is true in any sense in Ankh-Morpork, I don't know it.
So why does Vimes think those thoughts? I don't have a Watsonian explanation. One possible Doylist explanation is that Pratchett put it in the book because he wanted to comment on 20th Century Earth Anglosphere economics, and didn't notice or didn't care that it didn't make sense in context.
…but as someone who thinks it also doesn't make sense for 20th Century Earth Anglosphere economics, I think there's a slightly different explanation.
I think boots theory is a very foolish thing for Sam to believe of Ankh-Morpork, or for Pratchett to believe of Earth. But for whatever reason, lots of people do seem to believe it of Earth.
Or more accurately, lots of people interpret the description of boots theory as pointing at something they believe. I think they're wrong about some combination of "what those words mean" and "what is true" (and different people are wrong in different ways), but the point right now is that this is a thing lots of people do.
And if lots of people make a certain mistake about Earth, then it's also plausible that Pratchett made the same mistake about Ankh-Morpork, and inserted that mistake into Vimes' head. Or that Pratchett didn't make that mistake, but knew that lots of other people do, and deliberately inserted it into Vimes' head knowing it was a mistake.
So some possible theories are:
-
Pratchett, wanting to comment on Earth, had Vimes think thoughts about Earth but substituted in Ankh-Morpork. Pratchett didn't notice or didn't care that those thoughts were false when thought about Ankh-Morpork.
-
Pratchett had Vimes think untrue thoughts about Ankh-Morpork, that Pratchett thought were true about Ankh-Morpork. He thought that for the same reason that lots of people think the same thoughts would be true of Earth.
-
Pratchett had Vimes think untrue thoughts about Ankh-Morpork, that Pratchett knew were false about Ankh-Morpork; but Pratchett thought it was a believable mistake for Vimes to make, because Pratchett had seen people making the same mistake about Earth.
But ultimately I'll probably never know, and it doesn't really matter.
Posted on 18 March 2025
|
Comments
I sometimes see people describe the Elm community as "very active". For example:
- Elmcraft says "The
Elm community is very active."
- "Is Elm dead?" says "the community is more active than ever." (I guess that's compatible with "but still not very active", but, well, subtext.)
- Some /r/elm commenter says "The community is very active and productive." (They later clarify: "It's very active compared to similar projects. Tight focus, feature complete. People tend to compare it to dissimilar projects.")
Is this true? Let's get some statistics, including historical ones, and see what comes up.
I think all this data was collected on October 28 2024. I'm splitting things out by year, so we can roughly extrapolate to the end of 2024 by multiplying numbers by 1.2.
Subreddit
I could export 951 posts from reddit. (That's a weird number; I suspect it means there were 49 posts I couldn't see.) The oldest were in December 2019, which means I have about 4⅚ years of data. In a given calendar year, I can easily count: how many posts were there? And how many comments were there, on posts made in that calendar year? (So a comment in January 2022 on a post from December 2021, would be counted for 2021.)
| Year |
Posts |
Comments |
| 2020 |
296 |
2156 |
| 2021 |
236 |
1339 |
| 2022 |
215 |
1074 |
| 2023 |
132 |
639 |
| 2024 (extrapolated) |
76 |
505 |
| 2024 (raw) |
63 |
421 |
By either measure, 2024 has about a quarter of 2020 activity levels.
Discourse
I got a list of every topic on the discourse, with its creation date, "last updated" date (probably date of last reply in most cases), number of replies and number of views. The first post was in November 2017.
| Year |
Posts (C) |
Replies (C) |
Views (C) |
Posts (U) |
Replies (U) |
Views (U) |
| 2017 |
46 |
366 |
90830 |
29 |
151 |
46081 |
| 2018 |
819 |
5273 |
1634539 |
817 |
5284 |
1617704 |
| 2019 |
685 |
4437 |
1113453 |
695 |
4488 |
1137001 |
| 2020 |
610 |
4104 |
882214 |
613 |
4201 |
908361 |
| 2021 |
482 |
3502 |
603199 |
485 |
3528 |
608075 |
| 2022 |
332 |
1698 |
336095 |
329 |
1548 |
319918 |
| 2023 |
294 |
1544 |
221806 |
298 |
1711 |
243834 |
| 2024 (extrapolated) |
224 |
1422 |
115503 |
227 |
1438 |
116898 |
| 2024 (raw) |
187 |
1185 |
96253 |
189 |
1198 |
97415 |
The "C" columns count according to a post's creation date, and the "U" columns count by "last updated" date.
So posts and replies have fallen to about 35% of 2020 levels. Views have fallen to about 15%.
Package releases
For every package listed on the repository, I got the release dates of all its versions. So we can also ask how frequently packages are getting released, and we can break it up into initial/major/minor/patch updates.
My understanding is: if a package has any version compatible with 0.19, then every version of that package is listed, including ones not compatible with 0.19. If not it's not listed at all. So numbers before 2019 are suspect (0.19 was released in August 2018).
| Year |
Total |
Initial |
Major |
Minor |
Patch |
| 2014 |
1 |
1 |
0 |
0 |
0 |
| 2015 |
130 |
24 |
28 |
31 |
47 |
| 2016 |
666 |
102 |
137 |
145 |
282 |
| 2017 |
852 |
170 |
147 |
208 |
327 |
| 2018 |
1897 |
320 |
432 |
337 |
808 |
| 2019 |
1846 |
343 |
321 |
373 |
809 |
| 2020 |
1669 |
288 |
343 |
366 |
672 |
| 2021 |
1703 |
225 |
385 |
359 |
734 |
| 2022 |
1235 |
175 |
277 |
289 |
494 |
| 2023 |
1016 |
155 |
223 |
255 |
383 |
| 2024 (extrapolated) |
866 |
137 |
167 |
204 |
359 |
| 2024 (raw) |
722 |
114 |
139 |
170 |
299 |
Package releases have declined by about half since 2020. Initial (0.48x) and major (0.49x) releases have gone down slightly faster than minor (0.56x) and patch (0.53x) ones, which might mean something or might just be noise.
Where else should we look?
The official community page gives a few places someone might try to get started. The discourse and subreddit are included. Looking at the others:
- The twitter has had two posts in 2024, both in May.
- Elm weekly, from a quick glance, seems to have had more-or-less weekly posts going back many years. Kudos!
- I once joined the slack but I don't know how to access it any more, so I can't see how active it is. Even if I could, I dunno if I could see how active it used to be.
- I don't feel like trying to figure out anything in depth from meetup. I briefly note that I'm given a list of "All Elm Meetup groups", which has six entries, of which exactly one appears to be an Elm meetup group.
- I'm not sure what this ElmBridge thing is.
For things not linked from there:
- I'm aware that Elm Camp has run twice now, in 2023 and 2024, and is planning 2025.
- There's an Elm online meetup which lately seems to meet for approximately four hours a year.
- There are nine other Elm meetups listed on that site. Most have had no meetups ever; none of them have had more than one in 2024.
- The Elm radio podcast hasn't released an episode in 2024. Elm town seems roughly monthly right now.
- hnhiring.com shows generally 0-1 Elm jobs/month since 2023. There was also a dry spell from April 2019 to November 2020, but it's clearly lower right now than in 2018, 2021 and 2022.
- Elmcraft is a website that I think is trying to be a community hub or something? Other than linking to Elm Weekly and the podcasts, it has a "featured article" (from April) and "latest videos" (most recently from 2023).
- How many long-form articles are being written about Elm? Not sure if there's an easy way to get stats on this.
- The elm tag on StackOverflow has had 6 questions asked this year, 22 in 2023. I couldn't be bothered to count further back.
- Github also lets you search for "repositories written partially in language, created between date1 and date2". So e.g. elm repos created in 2023. Quick summary: 2.6k in 2019; 2.3k in 2020; 1.7k in 2021; 1.5k in 2022; 1.2k in 2023; 731 so far in 2024 (extrapolate to 877).
My take
I do not think the Elm community is "very active" by most reasonable standards. For example:
- I think that if someone asks me for a "very active" programming language community they can join, and I point them at the Elm community, they will be disappointed.
- I think that if I were to look for an Elm job, I would struggle to find people who are hiring.
- I couldn't find a single Elm meetup that currently runs anywhere close to monthly, either online or anywhere in the world.
- It seems like I could read literally every comment and post written on the two main public-facing Elm forums, in about ten minutes a day. If I also wanted to read the long-form articles, when those are linked… my guess is still under twenty minutes?
If you think you have a reasonable standard by which the Elm community counts as "very active", by all means say so.
I think the idea that the Elm community is "more active than ever" is blatantly false. (That line was added in January 2022, at which point it might have been defensible. But it hasn't been removed in almost three years of shrinking, while the surrounding text has been edited multiple times.)
To be clear, none of this is intended to reflect on Elm as a language, or on the quality of its community, or anything else. I do have other frustrations, which I may or may not air at some point. But here I just intend to address the question: is it reasonable to describe the Elm community as "very active"?
(I do get the vibe that the Elm community could be reasonably described as "passionate", and that that can somewhat make up for a lack of activity. But it's not the same thing.)
Posted on 02 November 2024
|
Comments
Translated by Emily Wilson
1.
I didn't know what the Iliad was about. I thought it was the story of how Helen of Troy gets kidnapped, triggering the Trojan war, which lasts a long time and eventually gets settled with a wooden horse.
Instead it's just a few days, nine years into that war. The Greeks are camped on the shores near Troy. Agamemnon, King of the Greeks, refuses to return a kidnapped woman to her father for ransom. (Lots of women get kidnapped.) Apollo smites the Greeks with arrows which are plague, and after a while the other Greeks get annoyed enough to tell Agamemnon off. Achilles is most vocal, so Agamemnon returns that woman but takes one of Achilles' kidnapped women instead.
Achilles gets upset and decides to stop fighting for Agamemnon. He prays to his mother, a goddess, wanting the Greeks to suffer ruin without him. She talks to Zeus, who arranges the whole thing, though Hera (his wife and sister) and Athena aren't happy about it because they really want Troy sacked.
So Zeus sends a dream to Agamemnon, telling him to attack Troy. Agamemnon decides to test the Greek fighters, telling them it's time to give up and sail home. So they start running back to the ships, but Athena tells Odysseus to stop them, which he does mostly by telling them to obey orders.
There's a bunch of fighting between Greeks and Trojans, and bickering among the gods, and occasionally mortals even fight gods. In the middle of it there's a one-day truce, which the Greeks use to build a wall, complete with gates. Poseidon says it's such a good wall that people will forget the wall of Troy, which upsets him because they didn't get the gods' blessing to build it. Agamemnon tries to convince Achilles to fight again by offering massive rewards, including the woman he stole earlier, whom he swears he has not had sex with as is the normal way between men and women.
Eventually the Trojans fight past the wall and reach the Greek fleet. At this point Patroclus, Achilles' bff (not explicitly lover, but people have been shipping them for thousands of years), puts on Achilles' armor and goes to fight. He's skilled and scary enough that the Trojans flee. Achilles told him not to chase them, but he does so anyway, and he's killed by Hector. Hector takes the weapons and armor, and there's a big fight for his body, but the Greeks manage to drag it back to their camp.
When Achilles finds out he's pissed. The god Hephaestus makes him a new set of weapons and armor, Agamemnon gives him the massive reward from earlier, and he goes on a killing spree. He briefly gets bored of that and stops to capture twelve Trojan kids, but quickly resumes. Eventually all the Trojans except Hector flee into Troy. He kills Hector and drags the body around the city then back to camp. There's a funeral for Patroclus, which includes killing those twelve kids, but then every morning he just keeps dragging Hector's body around Patroclus' pyre. The gods don't let it get damaged, but this is still extremely poor form.
Eventually the gods get Hector's father Priam to go talk to him. Hermes disguises himself as a super hot Greek soldier to guide Priam to Achilles' tent. Priam begs and also offers a large ransom, and Achilles returns the body and gives them twelve days for a funeral before the fighting restarts. Most of this is gathering firewood.
2.
Some excerpts.
Diomedes meets Glaucus on the battlefield, and asks his backstory to make sure he's not a god. Glaucus tells the story of his grandfather Bellerophon, and Diomedes realizes that his own grandfather had been friends with Bellerophon:
The master of the war cry, Diomedes,
was glad to hear these words. He fixed his spear
firm in the earth that feeds the world, and spoke
in friendship to the shepherd of the people.
"So you must be an old guest-friend of mine,
through our forefathers. Oeneus once hosted
noble Bellerophon inside his house
and kept him as his guest for twenty days.
They gave each other splendid gifts of friendship.
Oeneus gave a shining belt, adorned
with purple, and Bellerophon gave him
a double-handled golden cup. I left it
back home inside my house when I came here.
But I do not remember Tydeus.
He left me when I was a tiny baby,
during the war at Thebes when Greeks were dying.
Now you and I are also loving guest-friends,
and I will visit you one day in Argos,
and you will come to visit me in Lycia,
whenever I arrive back home again.
So let us now avoid each other's spears,
even amid the thickest battle scrum.
Plenty of Trojans and their famous allies
are left for me to slaughter, when a god
or my quick feet enable me to catch them.
And you have many other Greeks to kill
whenever you are able. Let us now
exchange our arms and armor with each other,
so other men will know that we are proud
to be each other's guest-friends through our fathers."
With this, the two jumped off their chariots
and grasped each other's hands and swore the oath.
Then Zeus robbed Glaucus of his wits. He traded
his armor with the son of Tydeus,
and gave up gold for bronze—gold armor, worth
a hundred oxen, for a set worth nine.
At one point Hera dolls herself up to make Zeus want to sleep with her. This is the flirting game of Zeus, greatest of all the gods:
"You can go later on that journey, Hera,
but now let us enjoy some time in bed.
Let us make love. Such strong desire has never
suffused my senses or subdued my heart
for any goddess or for any woman
as I feel now for you. Not even when
I lusted for the wife of Ixion,
and got her pregnant with Pirithous,
a councillor as wise as any god.
Not even when I wanted Danae,
the daughter of Acrisius, a woman
with pretty ankles, and I got her pregnant
with Perseus, the best of warriors.
Not even when I lusted for the famous
Europa, child of Phoenix, and I fathered
Minos on her, and godlike Rhadamanthus.
Not even when I wanted Semele,
or when in Thebes I lusted for Alcmene,
who birthed heroic Heracles, my son—
and Semele gave birth to Dionysus,
the joy of mortals. And not even when
I lusted for the goddess, Queen Demeter,
who has such beautiful, well-braided hair—
not even when I wanted famous Leto,
not even when I wanted you yourself—
I never wanted anyone before
as much as I want you right now. Such sweet
desire for you has taken hold of me."
3.
It feels kinda blasphemous to say, but by modern standards, I don't think the Iliad is very good. Sorry Homer.
Not that there's nothing to like. I enjoyed some turns of phrase, though I don't remember them now. And it was the kind of not-very-good that still left me interested enough to keep listening. I'm sure there's a bunch of other good stuff to say about it too.
But also a lot that I'd criticize, mostly on a technical level. The "what actually happens" of it is fine, but doesn't particularly stand out. But the writing quality is frequently bad.
A lot of the fighting was of the form: Diomedes stabbed (name) in the chest. He was from (town) and had once (random piece of backstory), and he died. (Name) was killed by Diomedes, who stabbed him in the throat; his wife and children would never see him again. Then Diomedes stabbed (name) in the thigh, …
So I got basically no sense of what it was like to be on the battlefield. How large was it? How closely packed are people during fighting? How long does it take to strip someone of their armor and why isn't it a virtual guarantee that someone else will stab you while you do? The logistics of the war are a mystery to me too: how many Greeks are there and where do they get all their food? We're told how many ships each of the commanders brought, but how many soldiers and how many servants to a ship?
I also had very little sense of time, distance, or the motivations or powers of the gods.
There were long lists that bored me, and sometimes Homer seemed to be getting paid by the word—lots of passages were repeated verbatim, and a few repeated again. (Agamemnon dictates the reward he'll offer Achilles to a messenger, then the messenger passes it on to Achilles, and we're told it again after Patroclus' death.)
We're often told that some characters are the best at something or other, but given little reason to believe it. Notably, Hector is supposedly the most fearsome Trojan fighter, but he doesn't live up to his reputation. He almost loses one-on-one against Ajax before the gods intervene to stop the battle; he gets badly injured fighting Ajax again; and even after being healed, he only takes down Patroclus after Patroclus has been badly wounded by someone else. And Achilles is supposed to be the fastest runner, but when he chases after Hector, he doesn't catch up until Hector stops running away. Lots of people are described as "favored by Zeus" but Zeus doesn't seem to do jack for them.
Even when the narrative supports the narrator, it feels cheap. Achilles is supposedly the best Greek fighter, and when he fights, he wins. So that fits. But how did he become so good at it? Did he train harder? Does he have some secret technique? Supernatural strength? We're not told. (His invulnerability-except-heel isn't a part of this story, and half of everyone is the son of some god or goddess so that's no advantage to him. To be fair: a reader points out that Superman stories don't necessarily give his backstory either.)
The poem is in iambic pentameter, with occasional deviations at the beginnings and ends of lines. I guess that's technically impressive, but I mostly didn't notice. I also didn't notice any pattern in where the line breaks occur, so the "pentameter" part of it seems mostly irrelevant. If it had been unmetered, I don't think I would have enjoyed it noticeably less.
Is this just my personal tastes, such that other people would really enjoy the book? I dunno, probably at least a bit, and I've spoken to at least one person who said he did really enjoy it. Still, my honest guess is that if the Iliad was published for the first time today, it wouldn't be especially well received.
If it's not just me, is the problem that writers today are better at writing than writers a long time ago? Or that they're operating under different constraints? (The Iliad was originally memorized, and meter and repetition would have helped with that.) Or do readers today just have different tastes than readers a long time ago? I don't know which of these is most true. I lean towards "writers are better" but I don't really want to try making the argument. I don't think it matters much, but feel free to replace "the Iliad isn't very good by modern standards" with "the Iliad doesn't suit modern tastes" or "isn't well optimized for today's media ecosystem".
And how much is the original versus the translation, or even the narrator of the audiobook? I still don't know, but the translation is highly praised and the narration seemed fine, so I lean towards blaming the original.
4.
What is up with classics?
Like, what makes something a classic? Why do we keep reading them? Why did it feel vaguely blasphemous for me to say the Iliad isn't very good?
I'm probably not being original here, but….
I think one thing often going on is that classics will be winners of some kind of iterated Keynesian beauty contest. A Keynesian beauty contest is one where judges have incentive to vote, not for the person they think is most beautiful, but the person they think the other judges will vote for. Do a few rounds of those and you'll probably converge on a clear winner; but if you started over from scratch, maybe you'd get a different clear winner.
(I vaguely recall hearing about experiments along the lines of: set up some kind of Spotify-like system where users can see what's popular, and run with a few different isolated sets of users. In each group you get clear favorites, but the favorites aren't the same. If true, this points in the direction of IKBC dynamics being important.)
But what contests are getting run?
A cynical answer is that it's all signaling. We read something because all the educated people read it, so it's what all the educated people read. I'm not cynical enough to think this is the whole story behind classics, or even most of it, but it sure seems like it must be going on at least a little bit.
(Of course we're not going to get a whole crowd of admirers to admit "there's nothing here really, we just pretend to like this to seem sophisticated". So even if this is most of the story, we might not expect to find a clear example.)
To the extent that this is going on, then we'd expect me to be scared to criticize the Iliad because that exposes me as uneducated. Or we might expect me to criticize it extra harshly to show how independent-minded I am. Or both! And in fact I don't fully trust myself to have judged it neutrally, without regard to its status.
My guess: this is why some people read the Iliad, but it's not the main thing that makes it a classic.
Less cynically, we might observe that classics are often referenced, and we want to get the references. I don't think this could make something a classic in the first place, but it might help to cement its status.
In fact, it's not a coincidence that I listened to the Iliad soon after reading Terra Ignota. I don't really guess this is a large part of why others read it, but maybe.
(Also not a coincidence that I read A Midsummer Night's Dream soon after watching Get Over It. Reading the source material radically changed my opinion of that film. It went from "this is pretty fun, worth watching" to "this is excellent, one of my favorite movies". Similarly, See How They Run was improved by having recently seen The Mousetrap.)
A closely related thing here is that because lots of other people have read the classics, they've also written about the classics and about reading the classics. So if you enjoy reading commentary on the thing you've just read, the classics have you covered.
Some things might be classics because they're just plain good. There was a lot of crap published around the same time, and most of it has rightly been forgotten, but some was great even by the standards of today.
Like, maybe if you published Pride and Prejudice today, it would be received as "ah yes, this is an excellent entry in the niche genre of Regency-era romance. The few hundred committed fans of that genre will be very excited, and people who dabble in it will be well-advised to pick this one out".
But as I said above, I don't think the Iliad meets that bar.
I would guess the big thing for the Iliad is that it's a window into the past. Someone might read Frankenstein because they're interested in early science fiction, or because they want to learn something about that period in time. And someone might read the Iliad because they're interested in early literature or ancient Greece.
(And this might explain why classics often seem to be found in the non-fiction section of the library or bookstore. It's not that they're not fiction, but they're not being read as fiction.)
5.
The trouble is, that needs a lot of context. And I don't know enough about ancient Greece to learn much from the Iliad. I did learn a bit—like, apparently they ate the animals they sacrificed! I guessed that that was authentic, and it was news to me.
But when Priam insults his remaining sons, is that a normal thing for him to do or are we meant to learn from this that Priam is unusually deep in grief or something?
Do slaves normally weep for their captors, or does that tell us that Patroclus was unusually kind to them?
When Diomedes gets injured stripping someone of his armor, did that happen often? Is Homer saying "guys this macho bullshit is kinda dumb, kill all the other guys first and then take the armor"?
When Nestor says "no man can change the mind of Zeus", and then shortly afterwards Agamemnon prays to Zeus and Zeus changes his mind, I can't tell if that's deliberate irony or bad writing or what.
I don't even know if the early listeners of the Iliad thought these stories were true, or embellishments on actual events, or completely fabricated.
Consider Boston Legal, which ran from 2004-2008, because that happens to be the show I'm watching currently. I think I understand what the writers were going for.
The show asks the question "what if there were lawyers like Alan Shore and Denny Crane". It doesn't ask the question "what if there were lawyers"—we're expected to take that profession as a background fact, to know that there are real-life lawyers whose antics loosely inspired the show. We're not supposed to wonder "why are people dressed in those silly clothes and why don't they just solve their problems by shooting each other". (Well, Denny does sometimes solve and/or cause his problems by shooting people, but.)
It explores (not very deeply) the conflicts between professional ethics and doing the right thing, and I think that works best if we understand that the professional ethics on the show aren't something the writers just made up. I'm not sure how closely they resemble actual lawyerly professional ethics, but I think they're a good match for the public perception of lawyerly professional ethics.
It shows us a deep friendship between a Democrat and a Republican, assuming we get the context that such things are kinda rare. When Denny insists that he's not gay, that marks him as mildly homophobic but not unusually so. When they have (sympathetic!) episodes on cryonics and polyamory, we're expected to know that those things are not widely practiced in society; the characters' reactions to them are meant to read as normal, not as "these characters are bigoted".
(Boston Legal also has a lot of sexual harassment, and honestly I don't know what's up with that.)
One way to think of fiction is that it's about things that might happen, that might also happen differently. It's not just significant "what happened" but "what didn't happen; what was the space of possibilities that the actual outcome was drawn from". In Boston Legal I know a lot of ways things might turn out, which means when I'm watching I can make guesses about what's going to happen. And when it does happen, I can be like "okay yeah, that tracks"—even if I hadn't thought of it myself, I can see that it fits, and I can understand why the writers might have chosen that one. In the Iliad I don't know the space of possibilities, so when something happens I'm like "okay, I guess?"
Or: fiction is in the things we're shown, and the things we're not shown even though they (fictionally) happened, and the things we're not shown because they didn't happen. Why one thing is shown and another is unshown and another doesn't happen is sometimes a marked choice and sometimes unmarked. (That is, sometimes "the writers did this for a specific reason and we can talk about why" and sometimes "this was just kind of arbitrary or default".) And if you can't read the marks you're going to be very confused.
-
Shown, unmarked: the lawyers are wearing suits. Marked: Edwin Poole isn't wearing pants.
-
Not-shown, unmarked: people brush their teeth. Marked: an episode ends when the characters are waiting for an extremely time-sensitive call to be answered, and we just never learn what happened.
-
Doesn't happen, unmarked: someone turns into a pig in the courtroom. Marked: someone reports a colleague to the bar for violating professional ethics. (At least not as far as I've watched.)
I can't read the marks in the Iliad. I don't know what parts of what it shows are "this is how stuff just is, in Homer's world" and what parts of it are "Homer showing the audience something unusual". That makes it difficult for me to learn about ancient Greece, and also makes it difficult to know what story Homer is telling.
I listened to the audiobook of the Iliad because I happened to know that it was originally listened-to, not read, so it seemed closer to the intended experience. But in hindsight, I can't get the intended experience and I shouldn't have tried.
I think to get the most out of the Iliad, I should have read it along with copious historical notes, and deliberately treated it as "learning about ancient Greece" at least as much as "reading a fun story".
Originally submitted to the ACX book review contest 2024; not a finalist. Thanks to Linda Linsefors and Janice Roeloffs for comments.
Posted on 18 June 2024
|
Comments
Quick note about a thing I didn't properly realize until recently. I don't know how important it is in practice.
tl;dr: Conditional prediction markets tell you "in worlds where thing happens, does other-thing happen?" They don't tell you "if I make thing happen, will other-thing happen?"
Suppose you have a conditional prediction market like: "if Biden passes the DRESS-WELL act, will at least 100,000 Americans buy a pair of Crocs in 2025?" Let's say it's at 10%, and assume it's well calibrated (ignoring problems of liquidity and time value of money and so on).
Let's even say we have a pair of them: "if Biden doesn't pass the DRESS-WELL act, will at least 100,000 Americans buy a pair of Crocs in 2025?" This is at 5%.
This means that worlds where Biden passes the DRESS-WELL act have a 5pp higher probability of the many-Crocs event than worlds where he doesn't. (That's 5 percentage points, which in this case is a 100% higher probability. I wish we had a symbol for percentage points.)
It does not mean that Biden passing the DRESS-WELL act will increase the probability of the many-Crocs event by 5pp.
I think that the usual notation is: prediction markets tell us
\[ P(\text{many-Crocs}\, | \,\text{DRESS-WELL}) = 10\% \]
but they don't tell us
\[ P(\text{many-Crocs}\, | \mathop{do}(\text{DRESS-WELL})) = \, ?\% \]
One possibility is that "Biden passing the DRESS-WELL act" might be correlated with the event, but not causally upstream of it. Maybe the act has no impact at all; but he'll only pass it if we get early signs that Crocs sales are booming. That suggests a causal model
\[ \text{early-sales}
→ \text{many-Crocs}
→ \text{DRESS-WELL}
← \text{early-sales}
\]
with
\[ P(\text{many-Crocs}\, | \mathop{do}(\text{DRESS-WELL}))
= P(\text{many-Crocs})
\]
(I don't know if I'm using causal diagrams right. Also, those two "early-sales"es are meant to be the same thing but I don't know how to draw that.)
But here's the thing that triggered me to write this post. We can still get the same problem if the intervention is upstream of the event. Perhaps Biden will pass the DRESS-WELL act if he thinks it will have a large effect, and not otherwise. Let's say the act has a 50% chance of increasing the probability by 3pp and a 50% chance of increasing it by 5pp. Biden can commission a study to find out which it is, and he'll only pass the act if it's 5pp. Then we have
\[ \text{size-of-impact}
→ \text{many-Crocs}
← \text{DRESS-WELL}
← \text{size-of-impact} \\
P(\text{many-Crocs}\, | \mathop{do}(\text{DRESS-WELL})) = \, 9\%
\]
I expect that sometimes you want to know the thing that prediction markets tell you, and sometimes you want to know the other thing. Good to know what they're telling you, whether or not it's what you want to know.
Some other more-or-less fictional examples:
- If Disney sues Apple for copyright infringement, will they win? A high probability might mean that Disney has a strong case, or it might mean that Disney will only sue if they decide they have a strong case.
- If the Federal Reserve raises interest rates, will inflation stay below 4%? A high probability might mean that raising interest rates reliably decreases inflation; or it might mean that the Fed won't raise them except in the unusual case that they'll decrease inflation.
- If I go on a first date with this person, will I go on a second? A high probability might mean we're likely to be compatible; or it might mean she's very selective about who she goes on first dates with.
Posted on 03 April 2024
|
Comments
Mostly out of curiosity, I've been looking into how cryptocurrency is taxed in the UK. It's not easy to get what I consider to be a full answer, but here's my current understanding, as far as I felt like looking into it. HMRC's internal cryptoassets manual is available but I didn't feel like reading it all, and some of it seems out of date (e.g. page CRYPTO22110 seems to have been written while Ethereum was in the process of transitioning from proof-of-work to proof-of-stake). I also have no particular reason to trust or distrust the non-government sources I use here. I am not any form of accountant and it would be surprising if I don't get anything wrong.
My impression is HMRC tends to be pretty tolerant of people making good faith mistakes? In that if they audit you and you underpaid, they'll make you pay what you owe but you won't get in any other trouble. Maybe they'd consider "I followed the advice of some blogger who explicitly said he wasn't an accountant" to be a good faith mistake? I dunno, but if you follow my advice and get audited, I'd love to hear what the outcome is.
After I published, reddit user ec265 pointed me at another article that seems more thorough than this one. I wouldn't have bothered writing this if I'd found that sooner. I didn't spot anywhere where it disagrees with me, which is good.
Capital gains tax
Very loosely speaking, capital gains is when you buy something, wait a bit, and then sell it for a different price than you bought it for. You have an allowance which in 2023-24 is £6,000, so you only pay on any gains you have above that. The rate is 10% or 20% depending on your income.
But with crypto, you might buy on multiple occasions, then sell only some of what you bought. Which specific coins did you sell? There's no fact of the matter. But the law has an opinion.
Crypto works like stocks here. For stocks HMRC explains how it works in a document titled HS283 Shares and Capital Gains Tax (2023), and there's also manual page CRYPTO22200 which agrees.
The rule is that when you sell coins in a particular currency, you sell them in the following order:
- Any coins you bought that day;
- Any coins you bought in the following 30 days;
- Any coins you bought previously, averaged together as if you'd bought them all for the same price.
The "30 following days" thing is called the "bed and breakfasting" rule, and the point is to avoid wash sales where you try to deliberately pull forward a loss you haven't incurred yet incurred for tax purposes. Wikipedia says "Wash sale rules don't apply when stock is sold at a profit", but that doesn't seem to be true in the UK. The rule applies regardless of if you'd be otherwise selling for profit or loss.
The third bucket is called a "section 104 holding". Every time you buy coins, if they don't offset something in one of the other buckets, they go in a big pool together. You need to track the average purchase price of the coins in that pool, and when you sell, you take the purchase price to be that average. Selling doesn't affect the average purchase price of the bucket.
If there are transaction fees, they count towards the purchase price (i.e. increase the average price in the bucket) and against the sale price (i.e. decrease the profit you made). This detail isn't in HS283, but it's in a separately linked "example 3".
So suppose that at various (sufficiently distant) points in time, I
- buy 0.1 BTC for £100;
- buy 0.1 BTC for £110;
- sell 0.15 BTC for £200;
- buy 0.1 BTC for £300;
- sell 0.15 BTC for £50;
and each of these had £5 in transaction fees.
Then my section 104 holding contains:
- Initially empty.
- Then, 0.1 BTC purchased at a total of £105, average £1050/BTC.
- Then, 0.2 BTC purchased at a total of £220, average £1100/BTC.
- Then, 0.05 BTC purchased at a total of £55, average £1100/BTC.
- Here I sold 0.15 BTC purchased at a total of £165, and I sold them for £195 after fees, so that's £30 profit.
- Then, 0.15 BTC purchased at a total of £360, average £2400/BTC.
- Then, 0 BTC purchased at a total of £0, average meaningless.
- Here I sold 0.15 BTC purchased at a total of £360, and I sold them for £45 after fees, so that's £315 loss.
For the same-day bucket, all buys get grouped together and all sells get grouped together. For the 30-day bucket, you match transactions one at a time, the earliest buy against the earliest sell. (Unclear if you get to group them by day; I don't see anything saying you do, but if you don't then interactions with the same-day rule get weird.)
So for example, suppose the middle three events above all happened on the same day. In that case, it would work out as:
- My section 104 holding is initially empty.
- Then, it contains 0.1 BTC purchased at a total of £105, average £1050/BTC.
- Then we have three things happening on the same day.
- Grouping buys together, I buy 0.2 BTC for £420, average £2100/BTC.
- I sell 0.15 BTC from that bucket, which I bought for £315.
- Sale price is £195 so that's a loss of £120.
- The bucket now contains 0.05 BTC bought for £105, average £2100/BTC.
- That bucket enters my section 104 holding. This now contains 0.15 BTC purchased at a total of £210, average £1400/BTC.
- I sell my remaining BTC for £45, which is a loss of £165.
And if the middle three all happened within 30 days of each other, then:
- My section 104 holding is initially empty.
- Then, it contains 0.1 BTC purchased at a total of £105, average £1050/BTC.
- Then, 0.2 BTC purchased at a total of £220, average £1100/BTC.
- The subsequent buy and sell get matched:
- I buy 0.1 BTC for £305 and sell it for £130, making a loss of £175.
- I also sell 0.05 BTC for £65, that I'd bought at £55, making a profit of £10.
- So in total that sale makes me a loss of £165, and the 30-day bucket contains -0.05 BTC purchased at £55.
- That bucket enters my section 104 holding. This now contains 0.15 BTC purchased at a total of £165, average £1100/BTC.
- I sell my remaining BTC for £45, which is a loss of £120.
In all cases my total loss is £285, which makes sense. But I might get taxed differently, if this happened over multiple tax years.
Some more edge cases:
- I have no idea how these rules would apply if you're playing with options or short selling. I think those are both things you can do with crypto?
- If you receive crypto as a gift, you count it as coming in at market price on the day you recieved it. I'm not sure exactly how that's meant to be calculated (on any given day, lots of buys and sells happened for lots of different prices on various different legible exchanges; and lots also happened outside of legible exchanges) but I assume if you google "historical bitcoin prices" and use a number you find there you're probably good. So it's as if you were gifted cash and used it to buy crypto.
- Similarly, if you give it away as a gift, it's treated as disposing of it at market price on the day, as if you'd sold it for cash and gifted the cash.
- I think in both the above cases, if you buy or sell below market price as a favor (to yourself or the seller respectively) you still have to consider market price.
- If you trade one coin for another, you treat it as disposing of the first for GBP and buying the second for GBP. Mark both the sell and the buy at the market price of the second, so that if you're somehow trading £1000 of one coin for £1200 of another, £200 of profits is taxable now. I assume you also count fees for the sell, reducing your profit now.
Mining and staking
According to this site, mining and staking both count as income. (And so do capital gains, if you look like a professional trader.)
For mining, the market price at the time you recieve the coins counts as miscellaneous income. You can deduct "reasonable expenses" whatever that means. (Price of hardware? Electricity?)
For staking, you can either count it as miscellaneous income or savings income. These two have different tax-free allowances. Unclear if you can count some as miscellaneous and some as savings to use both? Again you can deduct "reasonable expenses" whatever that means.
This reddit thread suggests "savings interest or miscellaneous income?" is just a grey area, in which case I'd expect HMRC to be pretty tolerant of you choosing either but kinda ಠ_ಠ if they notice you trying to use both. It links to manual page CRYPTO21200 which sounds to me like it's just miscellaneous income. ec265 agrees.
I think the normal way staking works is that to get income, you need to lock your coins up for some period of time. New coins you receive are automatically locked, and when you want to do anything with them, you have to unlock them. So do you count as earning the coins when they arrive, or when you first unlock them? (When you initiate the unlocking, or when it completes?) "When they arrive" sounds like a pain in the ass, that can happen every few days with no engagement on your part and a different market price every time. But "when you unlock" has the same problem as CGT: are you unlocking coins you locked, or coins you earned, or what?
I assume it's "when they arrive" and you just gotta deal with that. Coinbase lets you download transaction history, including all staking rewards with market price in GBP at the time of receipt, so that's not so bad. But I've also played around with staking with Trust Wallet and I can't immediately see a way to get staking history from that. Sadly I didn't earn enough to worry about.
For capital gains purposes, it sounds like both mining and staking count the same as if you'd bought the coins for market price at the time you received them. That would mean they can go in the same-day bucket or the B&B bucket, for matching against coins sold.
Are stablecoins an exception?
The point of a stablecoin is to track a currency exactly. If I have 1 USDC, I should always be able to trade that for 1 USD, and vice versa. So should you treat any holdings in USDC the same as you'd treat a bank account denominated in USD?
I think this is relevant for three reasons:
- You don't need to worry about capital gains tax in foreign currency bank accounts.
- Coinbase pays interest on USDC. This isn't the same as staking, and it's not reported as staking in your transaction history. Interest in a foreign currency bank account counts as savings income, not miscellaneous income (see e.g. this HMRC forum answer).
- I guess it also counts as foreign income? That page isn't very clear, but I think the relevant question isn't "what currency are you getting interest in" but "what country is the bank account in". That probably depends on details of Coinbase's internal structure that I'm not familiar with; but probably they'd need to actively go to effort for UK users' USDC holdings to count as being in the UK, and probably if they did that they'd go out of their way to make sure I knew they do that, and I don't know they do it so probably they don't. If it's foreign income then it looks like that doesn't change how it's taxed, but you might need to report it differently.
I guess this means that if exchange rates don't go your way, you might end up with less money than you started but still have to pay tax, and not be able to offset your losses against capital gains.
…but I don't think that's actually how it works. It looks to me like stablecoins just get treated like any other crypto, based on this site:
Buying crypto with stablecoins is viewed as trading crypto for crypto, so any profits are subject to Capital Gains Tax.
and manual page CRYPTO10100, shortly after talking about stablecoins, saying:
HMRC does not consider cryptoassets to be currency or money.
So I think that no, stablecoins are not an exception. And I weakly guess that coinbase's USDC interest counts as miscellaneous (and non-foreign) income, not personal savings income, unless you decide that staking income is also personal savings income.
What if there's a fork?
Sometimes a cryptocurrency forks, and where you had one type of coin you now have two. How does that work?
Philosophically, I think the answer is: you always had both types of coin, it's just that no one was tracking the distinction between them. So on July 31 2017, I think that I have 0.1 BTC that I paid £100 for; on August 1 2017, I discover that actually I hold 0.1 BTC that I paid ??? for and 0.1 BCH that I paid ??? for, where the two ???s sum to £100.
(And when I sold 0.05 BTC for £30 a week previously, I actually sold 0.05 BTC and 0.05 BCH for amounts summing to £30, and it doesn't matter how they split at the time.)
In every case I know of, one of the split coins is considered the original and one is considered the fork. But I don't think there's a technical distinction there, it's just that there was a social (and sometimes legal) battle to decide who gets to use the original name and one group won that. ("Legal" example: when Ethereum Classic split off from Ethereum, the Ethereum Foundation had a trademark on the name. So whichever copy they endorsed was basically always going to get called "Ethereum", even if it turned out less popular.)
Of course, the outcomes of social-and-sometimes-legal battles can have important legal effects, even if there's no technical meaning to them. So one option would be to say that I paid £100 for 0.1 BTC, and £0 for 0.1 BCH. BTC has just had a drop in price (you can't reliably expect to sell 1 BTC + 1 BCH post-fork, for more than you could sell 1 BTC pre-fork), so your capital gains on BTC have gone down, but you can expect relatively high capital gains on BCH.
Another option would be to take the market price soon after they split. Suppose 1 BTC costs 9x as much as 1 BCH. Then we'd say I paid £90 for my BTC and £10 for my BCH.
This article recommends the second approach:
HMRC does not prescribe any particular apportionment method. It is standard practice (based on the treatment of shares, because cryptoassets use the same rules) that the cost of the original cryptoasset is apportioned between the old and new cryptoasset, pro-rata in line with the respective market values of each cryptoasset the day after the hard fork. …
HMRC has the power to enquire into an apportionment method that it believes is not just and reasonable. Therefore, whichever method an individual chooses to use, they should keep a record of this and be consistent throughout their tax returns.
Airdrops and NFTs
I don't even really know what airdrops are and I don't care how they're taxed, but I suppose some readers might so manual page CRYPTO21250 talks about them.
I don't care about NFTs either and didn't see a manual page on them, so ¯\_(ツ)_/¯.
Ledger
I like to track my finances with ledger, which means I want some way to encode these rules in that.
I think I have something that works decently, which I demonstrate in a sample file that you can see here.
I think it's mostly fairly standard outside of the Holdings top-level account. You can do e.g. ledger bal not Holdings to hide that. It doesn't make use of lot dates or prices to do matching (that's not how the UK needs you to do things). It doesn't use virtual postings.
It doesn't work in hledger because that doesn't support posting cost expressions like 0.01 ETH @ (£300 / 0.01). If you replace those with their calculated value it seems fine.
It should work fairly straightforwardly with stocks as well as crypto, with the caveat that I'm not sure how to encode stock splits and don't know if there are other fiddly details to complicate matters.
The things I'm most unhappy about are that it doesn't balance to 0, and that there's no help with average prices of Section 104 holdings.
Example ledger file
;; This ledger demonstrates calculating capital gains on cryptocurrency for UK
;; taxes. For more info see:
;; https://reasonableapproximation.net/2024/03/28/uk-crypto-taxes.html
2020/01/01 Buy
; When we buy an asset, we record it in two places. `Assets` holds what we
; currently own, grouped in some way that's convenient for general use (by
; which account they're in, currency, whatever). `Holdings` holds the same,
; but grouped by capital gains buckets.
;
; Annoyingly, they don't balance, since for capital gains purposes the price
; includes transaction fees. So the total ETH balance comes to 0 but the £
; balance comes to `Expenses:Fees`.
;
; The `@` and `@@` ensure the ETH and GBP amounts balance with each other.
; But the `Holdings` exchange rate is wrong, so we use `(@@)` to avoid that
; getting put in the price database.
;
; S104 is "Section 104". That's the technical term for that bucket.
Assets:ETH 0.13 ETH @ £765.38
Assets:GBP £-100.00
Expenses:Fees £0.50
Holdings:S104:ETH -0.13 ETH (@@) £100.00
Holdings:S104:ETH £100.00
2020/01/10 Buy
; So after this, the "Holdings:S104:ETH" account records that we own 0.21
; ETH, that we paid £200.00 for.
Assets:ETH 0.08 ETH @ £1243.75
Assets:GBP £-100.00
Expenses:Fees £0.50
Holdings:S104:ETH -0.08 ETH (@@) £100.00
Holdings:S104:ETH £100.00
2020/01/31 Staking
; When we get staking income, we can either record it as Income in ETH or £.
; Recording it as ETH seems more powerful, since it lets us answer all of:
;
; * "how much ETH have I got from staking?" (`ledger bal`)
; * "how much £ is that worth now?" (`ledger bal -X £`)
; * "how much was it worth when I got it?" (`ledger bal -X £ --historical`)
;
; Recording in £ would mean `ledger bal` fully balances in ETH (at least all
; buys and sells do), and total balance in £ equals `Expenses:Fees`. That
; seems like a potentially useful sanity check. We can at least check that
; non-staking transactions balance like that with
;
; ledger bal not @Staking
;
; Still, I'm not sure this is better than just recording in £.
;
; We don't need to add every staking distribution individually. We can group
; several together and add them all at once, as long as they don't need to
; be distinguished for capital gains or income tax reasons or something. But
; then the price isn't accurate, so we probably want to follow it with an
; explicit entry for the price on the final day.
Assets:ETH 0.0014 ETH
Income:Staking:ETH -0.0014 ETH
Holdings:S104:ETH -0.0014 ETH (@) £942.86
Holdings:S104:ETH £1.32
; This gives the actual price at the time we most recently received staking
; income. Price database entries given by `@` and `@@` are saved at midnight, so
; might as well use that time here too. We could equivalently leave out the
; time, `P 2020/01/31 ETH £981.38`.
P 2020/01/31 00:00:00 ETH £981.38
2020/02/05 Sell
; At this point, S104 holds 0.2114 ETH bought for a total of £201.32,
; average £952.32. That means 0.0514 ETH was bought for £48.95. I don't know
; if there's a way to have ledger help with that calculation or enforce that
; we did it right.
Assets:ETH -0.0514 ETH @ £1578.97
Assets:GBP £80.66
Expenses:Fees £0.50
Income:Capital Gains:ETH £-31.71
Holdings:S104:ETH 0.0514 ETH (@@) £80.66
Holdings:S104:ETH £-48.95
2020/03/01 Sell
; Now a more complicated sell that we'll match with some non-S104 buys.
;
; When we buy, we know by the end of the day which Holdings bucket(s) it
; needs to go in. But when we sell, any buys or other acquisitions in the
; next 30 days affect which bucket(s) we're drawing from. So we won't be
; able to complete this transaction until April. (The bed-and-breakfasting
; bucket for this sell runs March 2-31 inclusive.) Until we do we might
; choose to just write the Assets and Expenses postings, leaving the
; transaction not to balance in ETH until we come back and fill in the rest.
;
; This counts as a capital loss (positive income), since after transaction
; fees, we buy it back in future for slightly more than we sell it for now.
;
; The three +ETH and the three -£ in Holdings empty out those buckets, and
; in this case there's none left over to take from the S104 bucket. The
; `(@)`s ensure that if we get cap gains wrong, the whole thing won't
; balance.
Assets:ETH -0.08 ETH @ £1635.90
Assets:GBP £130.37
Expenses:Fees £0.50
Income:Capital Gains:ETH £1.06
Holdings:SameDay:20200301:ETH 0.01 ETH (@) (£130.37 / 0.08)
Holdings:SameDay:20200301:ETH £-16.71
Holdings:BnB:20200301:ETH 0.05 ETH (@) (£130.37 / 0.08)
Holdings:BnB:20200301:ETH £-80.45
Holdings:BnB:20200301:ETH 0.02 ETH (@) (£130.37 / 0.08)
Holdings:BnB:20200301:ETH £-34.27
; Suppose that the Mar 31 buy below didn't happen. Then the last 0.02 ETH
; here would come from the S104 bucket. At this point the bucket contains
; 0.16 ETH bought for £114.72, average £952.31. (It changed slightly in the
; last transaction because of rounding errors.) So 0.02 ETH was bought for
; £19.05. In that case the Income posting and the last two Holdings postings
; would be replaced with:
;
; Income:Capital Gains:ETH £-14.16
; Holdings:S104:ETH 0.02 ETH (@) (£130.37 / 0.08)
; Holdings:S104:ETH £-19.05
2020/03/01 Buy
; We buy some back on the very same day. This is within 30 days after the
; Feb 5 sell, but the sell from today takes precedence. If we bought more
; than 0.08 ETH here, then the remainder would go in a BnB bucket to match
; against that. After today, the `SameDay:20200301` account is empty.
Assets:ETH 0.01 ETH @ £1620.81
Assets:GBP £-16.71
Expenses:Fees £0.50
Holdings:SameDay:20200301:ETH -0.01 ETH (@@) £16.71
Holdings:SameDay:20200301:ETH £16.71
2020/03/07 Buy
; We buy some more back within 30 days after selling, so this is also
; matched against the Mar 1 buy. It's 31 days after Feb 5, so it doesn't
; get matched against that.
Assets:ETH 0.05 ETH @ £1599.01
Assets:GBP £-80.45
Expenses:Fees £0.50
Holdings:BnB:20200301:ETH -0.05 ETH (@@) £80.45
Holdings:BnB:20200301:ETH £80.45
2020/03/31 Buy
; And more on the final day in the BnB window. Only 0.02 ETH gets matched
; against the previous sale, the rest goes into the S104 bucket. After
; today, the `BnB:20200301` account is empty.
Assets:ETH 0.05 ETH @ £1703.67
Assets:GBP £-85.68
Expenses:Fees £0.50
Holdings:BnB:20200301:ETH -0.02 ETH (@) (£85.68 / 0.05)
Holdings:BnB:20200301:ETH £34.27
Holdings:S104:ETH -0.03 ETH (@) (£85.68 / 0.05)
Holdings:S104:ETH £51.41
Posted on 28 March 2024
|
Comments
Some months ago I got a 3D printer. (An Anycubic Kobra Go, which was pretty high up the list of "best value for money for a starter printer" that I found through /r/3Dprinting at the time.) I haven't used it much, but recently I used it to solve an itch. I wanted my headphones to be in easy reach, so I designed and printed a hook that I could slide over the edge of the table near my desk. This is the first thing I've designed and I'm pretty happy with how it came out!


The curve was pretty awkward. I was working with OpenSCAD (maybe something else would have been easier?) which doesn't have an easy way that I found to draw nice curves. (Lines in general seem annoying, you can extrude a 2d shape to 3d but not a 1d shape to 2d?)
I decided to go with an Archimedean spiral, and did a bunch of math to figure out how the various parameters had to relate to each other. I ended up with equations that I'd have had to solve numerically because they probably had no closed form. Then rather than writing a simple script to give me the answers I just eyeballed it, figuring I could redo it properly if I felt like it. Seems basically fine though.
I ended up printing three copies. The first had a nozzle jam about half way through so it came out shitty. You can see it in the background of the second pic. It actually works, but it doesn't have enough friction on the table so it sags down. I can use it for looping cable over, though a deeper hook would be better at that. The second was mostly fine, but I decided I wanted 100% infill on the curve for strength and for some reason I did that by making the walls thick. In hindsight that's silly, it's pretty flexible and when you bend it a bit it starts to split along the middle. So I did one with normal walls and normal 100% infill and it's absolutely fine. These two are the ones actually holding it up in the second picture, I might print a third to get less pressure on the padding.
I could have made something simpler if I wanted to fasten it to the table, either with screws or duct tape. But I like that it doesn't need that.
The exact design probably won't be any use to anyone who doesn't have the same model of cheap folding table as me. But in case it's interesting or helpful, here's the .scad:
Source code for the hook
top_depth = 1.5;
bottom_depth = 1.5;
vert_depth = 1.5;
hook_depth = 3;
width = 10;
top_length = 100;
edge_height = 15.54;
b1_length = 45;
support_height = 22.4;
b2_length = 16.3;
b3_length = 20;
hook_drop = 30;
rotate([90, 0, 0]) {
color("red")
cube([top_length + vert_depth, width, top_depth]);
color("yellow")
translate([top_length, 0, -edge_height])
cube([vert_depth, width, edge_height]);
color("red")
translate([top_length - b1_length, 0, -edge_height - bottom_depth])
cube([b1_length + vert_depth, width, bottom_depth]);
color("yellow")
translate([top_length - b1_length, 0, -edge_height - support_height])
cube([vert_depth, width, support_height - bottom_depth]);
color("red")
translate([top_length - b1_length - b2_length - vert_depth,
0,
-edge_height - support_height - bottom_depth])
cube([b2_length + 2*vert_depth, width, bottom_depth]);
color("yellow")
translate([top_length - b1_length - b2_length - vert_depth,
0,
-edge_height - support_height])
cube([vert_depth, width, support_height - bottom_depth]);
color("red")
translate([top_length - b1_length - b2_length - b3_length,
0,
-edge_height - bottom_depth])
cube([b3_length, width, bottom_depth]);
color("green")
translate([top_length + vert_depth,
width,
-edge_height - bottom_depth])
rotate([90, 0, 0])
scale([-1, 1, 1])
linear_extrude(width)
archimedean([+10,-58], 43, 0.15, -98, 98, width=3, $fn=180);
}
// https://openhome.cc/eGossip/OpenSCAD/ArchimedeanSpiral.html
module line(point1, point2, width = 1, cap_round_1 = true, cap_round_2 = true) {
angle = 90 - atan((point2[1] - point1[1]) / (point2[0] - point1[0]));
offset_x = 0.5 * width * cos(angle);
offset_y = 0.5 * width * sin(angle);
offset_1 = [offset_x, -offset_y];
offset_2 = [-offset_x, offset_y];
if (cap_round_1)
translate(point1) circle(d = width, $fn = 24);
if (cap_round_2)
translate(point2) circle(d = width, $fn = 24);
polygon(points=[
point1 + offset_1, point2 + offset_1,
point2 + offset_2, point1 + offset_2
]);
}
module polyline(points,
width = 1,
cap_round_1 = true,
cap_round_2 = true)
{
module polyline_inner(points, index) {
if(index < len(points)) {
line(points[index - 1], points[index], width,
cap_round_1 = index > 1 || cap_round_1,
cap_round_2 = index < len(points) - 1 || cap_round_2);
polyline_inner(points, index + 1);
}
}
polyline_inner(points, 1);
}
module archimedean(center, a, b, theta_1, theta_2, width=1, $fn=24) {
d_theta = (theta_2 - theta_1)/$fn;
thetas = [ for (i = [0:$fn]) theta_1 + i * d_theta ];
points = [ for (t = thetas) center + [(a + b * t)*cos(t), (a + b*t)*sin(t)] ];
polyline(points, width=width);
}
Posted on 29 September 2023
|
Comments
Suppose you have a game where you can bet any amount of money. You have a 60% chance of doubling your stake and a 40% chance of losing it.
Consider agents Linda and Logan, and assume they both have £1. Linda has a utility function that's linear in money (and has no other terms), \( U_\text{Linda}(m) = m \). She'll bet all her money on this game. If she wins, she'll bet it again. And again, until eventually she loses and has no more money.
Logan has a utility function that's logarithmic in money, \( U_\text{Logan}(m) = \ln(m) \). He'll bet 20% of his bankroll every time, and his wealth will grow exponentially.
Some people take this as a reason to be Logan, not Linda. Why have a utility function that causes you to make bets that leave you eventually destitute, instead of a utility function that causes you to make bets that leave you rich?
In defense of Linda
I make three replies to this. Firstly, the utility function is not up for grabs! You should be very suspicious any time someone suggests changing how much you value something.
"Because if Linda had Logan's utility function, she'd be richer. She'd be doing better according to her current utility function." My second reply is that this is confused. Before the game begins, pick a time \(t\). Ask Linda which distribution over wealth-at-time-\(t\) she'd prefer: the one she gets from playing her strategy, or Logan's strategy? She'll answer, hers: it has an expected wealth of \( £1.2^t \). Logan's only has an expected wealth of \( £1.04^t \).
And, at some future time, after she's gone bankrupt, ask Linda if she thinks any of her past decisions were mistakes, given what she knew at the time. She'll say no: she took the bet that maximized her expected wealth at every step, and one of them went against her, but that's life. Just think of how much money she'd have right now if it hadn't! (And nor had the next one, or the one after….) It was worth the risk.
You might ask "but what happens after the game finishes? With probability 1, Linda has no money, and Logan has infinite". But there is no after! Logan's never going to stop. You could consider various limits as \( t→∞ \), but limits aren't always well-behaved. And if you impose some stopping behavior on the game - a fixed or probabilistic round limit - then you'll find that Linda's strategy just uncontroversially gives her better payoffs (according to Linda) after the game than Logan's, when her probability of being bankrupt is only extremely close to 1.
Or, "but at some point Logan is going to be richer than Linda ever was! With probability 1, Logan will surpass Linda according to Linda's values." Yes, but you're comparing Logan's wealth at some point in time to Linda's wealth at some earlier point in time. And when Logan's wealth does surpass the amount she had when she lost it all, she can console herself with the knowledge that if she hadn't lost it all, she'd be raking it in right now. She's okay with that.
I suppose one thing you could do here is pretend you can fit infinite rounds of the game into a finite time. Then Linda has a choice to make: she can either maximize expected wealth at \( t_n \) for all finite \( n \), or she can maximize expected wealth at \( t_ω \), the timestep immediately after all finite timesteps. We can wave our hands a lot and say that making her own bets would do the former and making Logan's bets would do the latter, though I don't endorse the way we're treating infinties here.
Even then, I think what we're saying is that Linda is underspecified. Suppose she's offered a loan, "I'll give you £1 now and you give me £2 in a week". Will she accept? I can imagine a Linda who'd accept and a Linda who'd reject, both of whom would still be expected-money maximizers, just taking the expectation at different times and/or expanding "money" to include debts. So you could imagine a Linda who makes short-term sacrifices in her expected-money in exchange for long-term gains, and (again, waving your hands harder than doctors recommend) you could imagine her taking Logan's bets. But this is more about delayed gratification than about Logan's utility function being better for Linda than her own, or anything like that.
I'm not sure I've ever seen a treatment of utility functions that deals with this problem? (The problem being "what if your utility function is such that maximizing expected utility at time \(t_1\) doesn't maximize expected utility at time \(t_2\)?") It's no more a problem for Linda than for Logan, it's just less obvious for Logan given this setup.
So I don't agree that Linda would prefer to have Logan's utility function.
Counterattack
And my third reply is: if you think this is embarrassing for Linda, watch me make Logan do the same. Maybe not quite the same. I think the overall story matches, but there are notable differences.
I can't offer Logan a bet that he'll stake his entire fortune on. No possible reward can convince him to accept the slightest chance of running out of money. He won't risk his last penny to get \( £(3 ↑↑↑ 3) \), even if his chance of losing is \( 1 / (3 ↑↑↑↑ 3) \).
But I can offer him a bet that he'll stake all but a penny on. I can make the odds of that bet 60/40 in his favor, like the bets Linda was taking above, or any other finite probability. Then if he wins, I can offer him another bet at the same odds. And another, until he eventually loses and can't bet any more. And just like Linda, he'll be able to see this coming and he'll endorse his actions every step of the way.
How do I do this? I can't simply increase the payoff-to-stake ratio of the bet. If a bet returns some multiple of your stake, and has a 60% chance of winning, Logan's preferred amount to stake will never be more than 60% of his bankroll.
But who says I need to give him that option? Logan starts with £1, which he values at \( \ln(100) ≈ 4.6052 \). I can offer him a bet where he wagers £0.99 against £20.55 from me, with 60% chance of winning. He values that bet at
\[ 0.4\ln(100 - 99) + 0.6\ln(100 + 2055) ≈ 4.6053 \]
so he'll accept it. He'd rather wager some fraction of £0.99 against the same fraction of £20.55 (roughly £0.58 against £11.93), but if that's not on the table, he'll take what he can get.
If he wins he has £21.55 to his name, which he values at \( \ln(2155) ≈ 7.6755 \). So I offer him to wager £21.54 against my £3573.85, 60% chance of winning, which he values at… still \( 7.6755 \) but it's higher at the 7th decimal place. And so on, the stakes I offer growing exponentially - Logan is indifferent between a certainty of \( £x \) and a 60% chance of \( £x^{5/3} \) (plus 40% chance of £0.01), so I just have to offer slightly more than that (minus his current bankroll).
Admittedly, I'm not giving Logan much choice here. He can either bet everything or nothing. Can I instead offer him bets where he chooses how much of his money to put in, and he still puts in all but a penny? I'm pretty sure yes: we just need to find a function \( f : ℝ_{>0}^2 → ℝ_{>0} \) such that whenever \( a ∈ (0, x] \),
\[ \ln(x) < 0.4\ln(a) + 0.6\ln(f(x, a)) \\
{d \over d a}(0.4\ln(a) + 0.6\ln(f(x, a))) < 0 \]
Then if Logan's current bankroll is \( x \), I tell him that if he wagers \( w \), I'll wager \( f(x, x-w) - x \) (giving him 60% chance of coming away with \( f(x, x-w) \) and 40% chance of coming away with \( x-w \)). He'll want to bet everything he can on this. I spent some time trying to find an example of such a function but my math isn't what it used to be; I'm just going to hope there are no hidden complications here.
So what are the similarities and differences between Linda and Logan?
Difference: Logan's bets grow a lot faster than Linda's. For some fixed probability of bankrupting them, I need a lot less money for Linda than Logan. Similarity: I need an infinite bankroll to pull this off with probability 1, so who cares how fast the bets grow?
Difference: the structure of bets I'm offering Logan is really weird. Why on Earth would I offer him rewards exponential in his stake? Similarity: why on Earth would I offer any of these bets? They all lose money for me. Am I just a cosmic troll trying to bankrupt some utilitarians or something? (But the bets I'm offering Logan are still definitely weirder.)
Difference: I bring Linda down to £0.00, and then she'd like to bet more but she can't because she's not allowed to take on debt. I bring Logan down to £0.01, and then he'd like to bet more but he can't because he's not allowed to subdivide that penny. Similarity: these both correspond to "if your utility reaches 0 you have to stop playing".
(Admittedly, "not allowed to subdivide the penny" feels arbitrary to me in a way that "not allowed to go negative" doesn't. But note that Linda would totally be able to take on debt if she's seeing 20% return on investment. Honestly I think a lot of what's going on here, is that "not allowed to go negative" is something that's easy to model mathematically, while "not allowed to infinitely subdivide" is something that's hard to model.)
Difference: for Logan, but not for Linda, I need to know how much money he starts with for this to work. Or at least an upper bound.
But all of that feels like small fry compared to this big similarity. I can (given an infinite bankroll, a certain level of trollishness, and knowledge of Logan's financial situation) offer either one of them a series of bets, such that they'll accept every bet in turn and put as much money as they can on it; and then eventually they'll lose and have to stop betting. They'll know this in advance, and they'll play anyway, they'll lose all or almost all of their money, and they won't regret their decisions. If you think this is a problem for Linda's utility function, it's a problem for Logan's too.
What about a Kelly bettor?
I've previously made the case that we should distinguish between "maximizing expected log-money", the thing Logan does; and "betting Kelly", a strategy that merely happens to place the same bets as Logan in certain situations. According to my usage of the term, one bets Kelly when one wants to "rank-optimize" one's wealth, i.e. to become richer with probability 1 than anyone who doesn't bet Kelly, over a long enough time period.
It's well established that when offered the bets that ruin Linda, Kelly bets the same as Logan. But what does Kelly do when offered the bets that ruin Logan?
Well, I now realize that for any two strategies which make the same bet all but finitely many times, neither will be more rank-optimal than the other, according to the definition I gave in that post. That's a little embarrassing, I'm glad I hedged a bit when proposing it.
Still: when offered Logan's all-or-nothing bets, Kelly accepts at most a finite number of them. Any other strategy accepts an infinite number of them and eventually goes bankrupt with probability 1.
What about the bets where Logan got to choose how much he put in? Kelly would prefer to bet nothing (except a finite number of times) than to go all-in infinitely many times. But might she bet smaller amounts, infinitely often?
What are some possible strategies here? One is "bet a fixed amount every time"; this has some probability of eventually going bankrupt (i.e. ending up with less than the fixed amount), but I think the probability is less than 1. I don't think any of these strategies will be more or less rank-optimal than any of the others.
Another is "bet all but a fixed amount every time". This has probability 1 of eventually being down to that amount. Assuming you then stop, this strategy is more rank-optimal the higher that amount is (until it reaches your starting capital, at which point it's equivalent to not betting).
We could also consider "bet some fraction of (your current bankroll minus one penny)". Then you'll always be able to continue betting. My guess is that you'd have probability 1 of unboundedly increasing wealth, so any fraction here would be more rank-optimal than the other strategies, which can't guarantee ever turning a profit. Different fractions would be differently rank-optimal, but I'm not sure which would be the most rank-optimal. It could plausibly be unbounded, just increasing rank-optimality as the fraction increases until there's a discontinuity at 1. Or maybe the fraction shouldn't be fixed, but some function of her current bankroll.
…except that this is cheating a bit because it relies on infinite subdivisibility, and if we have that it's harder to justify the "can't bet below £0.01" thing.
So I think the answer is: Kelly will do the fractional-betting thing if she can, and if not she has no strategy she prefers over "never bet". In general, Kelly will only have a strategy she prefers over that, if she can lose arbitrarily often and still keep playing. (This is necessary but not sufficient.) Otherwise, there's some probability that she just keeps losing bets until she's out of the game; and Kelly really doesn't like that, no matter how small that probability is. Kelly has her own pathologies.
This makes me think that the technical definition of rank-optimality I suggested in the last post is not very useful here. Though nor is the technical definition of growth rate that the actual Kelly originally used.
My own strategy might be something like "bet some fraction, but if that would give me fewer than say 10 bets remaining then bet a fixed amount". That would give me a tiny chance of going bankrupt, but if I don't go bankrupt I'll be growing unboundedly. Also I'm not going to worry about the difference between £0.00 and £0.01.
Thanks to Justis Mills for commentary.
Posted on 20 August 2023
|
Comments
I gave a fifteen minute talk about this at Zurihac 2023. If you read this essay, I don't think there's much point in additionally watching the video.
I've been exploring a new-to-me approach to stringification. Except that right now it's three different approaches that broadly share a common goal. I call it/them pretty-gist.
The lowest-friction way to stringify things in Haskell is usually show. It gives the user close to zero ability to control how the thing is rendered.
The Show1 and Show2 classes give some control, but only in limited ways. Importantly, they only work on parameterized values; you could use Show2 to change how you render the keys of a Map Int String, but not of an IntMap String.
There are also things that give you some control over layout, but not much control over content. For example, aeson-pretty lets you pretty-print json data, and pretty-simple can pretty-print typical output from show. Both let you configure indent width, and pretty-simple additionally lets you choose some different layout styles (where to put newlines and parentheses) and stuff. But they both operate by a model where you produce a relatively simple data structure that they know how to deal with, they give you a few knobs and render it in full. (For aeson-pretty the data structure is JSON, for pretty-simple it's a custom type that they parse from show output and that's pretty good at reproducing it.)
Here are some use cases where I've wanted more control than I can easily get:
-
My test suites generate a complicated data structure. Most of the time, most of this data structure is irrelevant to the test failures and I don't want to see it.
-
A complicated data structure contains JSON values, and I want them rendered as JSON rather than as a Haskell data type. Or it contains floating-point numbers, and I want them rounded to 3dp with underscore separation (17_923.472). Or strings, which I want printed using C-style escapes rather than Haskell-style, and with unicode rendered.
-
A list might be infinite, and I only want to show the first ten elements. Or a tree might actually be cyclic, and I want to only show three levels deep.
pretty-gist aims to enable stuff like this. I call the rendered outputs it produces "gists" following Raku's use of that term, where I think the intention is something like "take a guess about what I'm likely to want to see here and show me that". But if pretty-gist guesses wrong, it lets you correct it.
I've come up with several different approaches to this, which all have different things to recommend and disrecommend them. I'm writing about three of them here.
If you're a Haskell user, I'm interested to hear your thoughts. I have some specific questions at the end.
Design goals
-
It should pretty-print, with indentation that adjusts to the available width.
-
As a user, you should be able to target configurations specifically or generally. "All lists" or "all lists of Ints" or "only lists found at this specific point in the data structure". "All floating-point numbers" or "Float but not Double".
-
It should be low boilerplate, both as a user and an implementer.
-
You shouldn't need extra imports to configure the rendering for a type.
-
If something almost works, you should be able to make it work. No need to throw everything out and start from scratch.
I don't know how to meet all these design goals at once, but they're things I aim for.
Also: I think there's a sort of hierarchy of demandingness for what sort of situations we expect to use the library in. From most to least demanding:
-
We're generating user-facing output, and we want to specify what it looks like down to the glyph.
-
We're generating debug output. We probably don't care about the exact layouting, but it would be unfortunate if we accidentally hid some data that we intended to include. We can't simply edit the config and retry.
-
We're generating output for a test failure. It's not ideal if it stops doing what we expect without warning, but it's not too bad because we can just change it and rerun the test.
-
We're writing debug code that we don't expect to commit.
In more demanding situations, we probably don't mind being more verbose, and updating our rendering code more often when the data structures we're working with change. In less demanding situations, we're more likely to be satisfied with an 80/20 of "not quite what I want but good enough".
I'm not personally working on anything where I care about glyph-level exactness, so that one isn't a situation I feel like optimizing for. The others are all things I'd like pretty-gist to help with, but of course the best design for one might not be the best design for the others.
Example
Here's how pretty-simple would render a particular representation of a chess game. Next to it is how I'd like pretty-gist to be able to, either by default or with a small amount of configuration on the user's part.
| pretty-simple |
pretty-gist |
GameState
{ turn = White
, pBlackWin = 0.3463
, pWhiteWin = 0.3896
, nMoves = 0
, board = Board
[
[ Just
( Piece
{ pieceType = Rook
, owner = Black
, lastMoved = Nothing
}
)
, Just
( Piece
{ pieceType = Knight
, owner = Black
, lastMoved = Nothing
}
...
|
GameState { turn = White
, pBlackWin = 35%
, pWhiteWin = 39%
, nMoves = 0
, board = [ [r, n, b, q, k, b, n, r]
, [p, p, p, p, p, p, p, p]
, [_, _, _, _, _, _, _, _]
, [_, _, _, _, _, _, _, _]
, [_, _, _, _, _, _, _, _]
, [_, _, _, _, _, _, _, _]
, [P, P, P, P, P, P, P, P]
, [R, N, B, Q, K, B, N, R]
]
}
|
So one difference is that I've gone with a hanging bracket style, with no newline directly after GameState or board =. I don't feel strongly about that. It would be nice to let users control this, but I haven't put much thought into it.
I've also rendered the floats as percents. I haven't put much thought into this either, and haven't implemented it. But it seems vaguely useful and easy enough to have as an option, though it usually shouldn't be default.
It's not visible here, but pretty-simple has the ability to colorize its output. That's another thing I haven't thought about, and don't currently expect pretty-gist to support any time soon.
But the most important is rendering each Maybe Piece as a single character. There are three parts to that: a Nothing is rendering as _; a Just is simply rendering the value it contains with no wrapper; and a Piece is rendering as a single character. The combination makes it much easier to see most of the state of the game. You can no longer see when each piece last moved. But if that's not usually useful to you, it's fine not to show it by default.
(At this point, chess pedants may be pointing out that this data type doesn't capture everything you need for chess. You can't reliably tell whether en passant is currently legal. Maybe there are other problems too. Yes, well done chess pedants, you're very clever, now shut up.)
Possible designs
I've come up with several possible designs for this making different tradeoffs. I'm going to talk about three of them that I've actually implemented to some extent.
Classless solution
Perhaps the very simplest solution is just to write a custom renderer every time I need one. I'm not going to do that.
A level up from that, which I've implemented in the module Gist.Classless, is to write renderers for lots of different data types and combine them. We can write
newtype Prec = Prec Int -- precedence level, 0 - 11
data ConfigMaybe = ConfigMaybe { showConstructors :: Bool }
gistMaybe :: ConfigMaybe -> (Prec -> a -> Doc) -> Prec -> Maybe a -> Doc
data ConfigList = ConfigList { showElems :: Maybe Int, ... }
gistList :: ConfigList -> (Prec -> a -> Doc) -> Prec -> [a] -> Doc
data ConfigTuple2 = ConfigTuple2 { ... }
gistTuple2
:: ConfigTuple2
-> (Prec -> a -> Doc)
-> (Prec -> b -> Doc)
-> Prec
-> (a, b)
-> Doc
data ConfigFloat = ConfigFloat { ... }
gistFloat :: ConfigFloat -> Prec -> Float -> Doc
for some data type Doc that supports layout. (I've been using the one from prettprinter, which has a type argument that I'm ignoring here for simplicity.)
The Prec parameters here are needed for the same reason Show has showsPrec. Sometimes we need parentheses, and this lets us choose when we have them. But they clutter things up a lot. We could imagine predence being something that gets put into config types, but then the user needs to specify it everywhere; plus, a renderer might call one of its sub-renderers at two different precedence levels under different circumstances. So that doesn't really work, so we accept the clutter.
But essentially, we've decided that one particular config parameter is important enough that every function accepts it (which means every function expects every other function to accept it). That feels kinda dirty. Is there anything else that ought to be given this treatment?
Anyway, this works, and it has some things to recommend it. It's incredibly simple, a beginner-level Haskell programmer will be able to figure out what's going on. If I, as the library author, make a decision you the library user don't like, you can just write your own function and it plugs in seamlessly. And if you have a type that can't normally be rendered, like a function, you can pick some way to render it anyway.
It also has some things to disrecommend it. Most notably, it's very verbose. You need to specify how to render every type-parameterized node of your data structure. You can have default configs, but there's no "default list renderer" because there's no "default list element renderer". IntMap v can have a default renderer for its keys, but Map Int v can't unless you write a function gistMapInt separate from gistMap.
This also means that changes to your data structure are very often going to need to be reflected in your renderers, which sounds tedious.
Another problem is, I expect consistency to be hard. Whatever design decisions I make, they're not enforced through anything. So someone who disagrees with them, or simply isn't paying attention to them, can easily make different ones, and then users need to remember things. (E.g. I had gistList, gistTuple2 and gistFloat all take precedence parameters, but they'll completely ignore them. So maybe someone in a similar situation decides not to bother with those parameters.)
Those are problems for users. There's also a problem for implementers: roughly speaking, you're going to be allowing the user to pass a renderer for every field of every constructor of your type. For non-parameterized types (like the keys of an IntMap) that can be in the actual config type, and for parameterized types (like the keys of a Map) it comes in separate arguments later, but it's going to be there. That's going to be tedious for you.
Implementation for Maybe
data ConfigMaybe = ConfigMaybe { showConstructors :: Bool }
deriving stock Generic
defaultConfigMaybe :: ConfigMaybe
defaultConfigMaybe = ConfigMaybe { showConstructors = False }
gistMaybe :: ConfigMaybe -> (Prec -> a -> Doc ann) -> Prec -> Maybe a -> Doc ann
gistMaybe (ConfigMaybe {..}) renderElem prec = if showConstructors
then \case
Nothing -> "Nothing"
Just a -> parensIf (prec > 10) $ "Just" <+> renderElem 11 a
else \case
Nothing -> "_"
Just a -> renderElem prec a
-- Renders "()".
gistMaybe defaultConfigMaybe (\_ _ -> "()") 0 $ Just ()
-- Renders "Just ()".
gistMaybe (defaultConfigMaybe { showConstructors = True })
(\_ _ -> "()")
0
$ Just ()
Implementation for GameState
import qualified Gist
import Gist ( Prec )
import qualified Gist as Gist.ConfigMaybe ( ConfigMaybe(..) )
data ConfigPiece = ConfigPiece
{ singleChar :: Bool
, renderPieceType :: forall ann . Prec -> PieceType -> Doc ann
, renderOwner :: forall ann . Prec -> Player -> Doc ann
, renderLastMoved :: forall ann . Prec -> Maybe Int -> Doc ann
}
defaultConfigPiece :: ConfigPiece
defaultConfigPiece = ConfigPiece
{ singleChar = False
, renderPieceType = Gist.gistShowily
, renderOwner = Gist.gistShowily
, renderLastMoved = Gist.gistMaybe Gist.defaultConfigMaybe Gist.gistShowily
}
gistPiece :: ConfigPiece -> Prec -> Piece -> Doc ann
gistPiece (ConfigPiece {..}) prec piece@(Piece {..}) = if singleChar
then prettyPieceChar piece
else Gist.record
prec
(Just "Piece")
[ ("pieceType", renderPieceType 0 pieceType)
, ("owner" , renderOwner 0 owner)
, ("lastMoved", renderLastMoved 0 lastMoved)
]
gistBoard :: (Prec -> [[a]] -> Doc ann) -> Prec -> Board a -> Doc ann
gistBoard renderer prec (Board a) = renderer prec a
data ConfigGameState = ConfigGameState
{ renderTurn :: forall ann . Prec -> Player -> Doc ann
, renderPBlackWin :: forall ann . Prec -> Float -> Doc ann
, renderPWhiteWin :: forall ann . Prec -> Float -> Doc ann
, renderNMoves :: forall ann . Prec -> Int -> Doc ann
, renderBoard :: forall ann . Prec -> Board (Maybe Piece) -> Doc ann
}
defaultConfigGameState :: ConfigGameState
defaultConfigGameState = ConfigGameState
{ renderTurn = Gist.gistShowily
, renderPBlackWin = Gist.gistShowily
, renderPWhiteWin = Gist.gistShowily
, renderNMoves = Gist.gistShowily
, renderBoard = gistBoard
$ Gist.gistList Gist.defaultConfigList
$ Gist.gistList Gist.defaultConfigList
$ Gist.gistMaybe Gist.defaultConfigMaybe
$ gistPiece
$ defaultConfigPiece { singleChar = True }
}
gistGameState :: ConfigGameState -> Prec -> GameState -> Doc ann
gistGameState (ConfigGameState {..}) prec (GameState {..}) = Gist.record
prec
(Just "GameState")
[ ("turn" , renderTurn 0 turn)
, ("pBlackWin", renderPBlackWin 0 pBlackWin)
, ("pWhiteWin", renderPWhiteWin 0 pWhiteWin)
, ("nMoves" , renderNMoves 0 nMoves)
, ("board" , renderBoard 0 board)
]
-- Renders in short form.
gistGameState defaultConfigGameState 0 startPos
-- Renders in long form.
let conf = defaultConfigGameState
{ renderBoard = gistBoard
$ Gist.gistList Gist.defaultConfigList
$ Gist.gistList Gist.defaultConfigList
$ Gist.gistMaybe Gist.defaultConfigMaybe
$ gistPiece
$ defaultConfigPiece { singleChar = False }
}
in gistGameState conf 0 startPos
-- Renders in fully explicit form.
let confMaybe =
Gist.defaultConfigMaybe { Gist.ConfigMaybe.showConstructors = True }
conf = CB.defaultConfigGameState
{ CB.renderBoard = CB.gistBoard
$ Gist.gistList Gist.defaultConfigList
$ Gist.gistList Gist.defaultConfigList
$ Gist.gistMaybe confMaybe
$ CB.gistPiece
$ CB.defaultConfigPiece
{ CB.singleChar = False
, CB.renderLastMoved = Gist.gistMaybe
confMaybe
Gist.gistShowily
}
}
in gistGameState conf 0 startPos
One-class solution
We can maybe-improve on this with typeclasses. We can use type families to let each gistable type have a separate config type.
class Gist a where
type Config a :: Type
defaultConfig :: Config a
gistPrec :: Prec -> Config a -> a -> Doc
data ConfigList a = ConfigList
{ showFirst :: Maybe Int
, configElem :: Config a
}
instance Gist a => Gist [a] where
type Config [a] = ConfigList a
defaultConfig = ConfigList { showFirst = Nothing, configElem = defaultConfig }
gistPrec = ...
This is the foundation of the approach I've implemented in the module
Gist.OneClass.
There are a few significant complications. One is, this won't handle String well, because that's just [Char]. Other typeclasses (including Show) solve this by having an extra method for "how to handle lists of this type"; then you give that method a default implementation, but override it for Char. This seems fine as a solution, by which I mean "I hate it but I don't have any better ideas". I'm not going to bother showing it here. (Also it's not actually implemented for this approach in the code yet.)
Next: the typechecking here doesn't work very well. If we try
gist (defaultConfig { ... }) [True] -- `gist` is `gistPrec 0`
we probably mean defaultConfig to refer to defaultConfig @[Bool]. But all GHC knows is that we mean defaultConfig { ... } to have type Config [Bool]. That doesn't even fully specify the type of defaultConfig, let alone its value. (We might be using the defaultConfig of some other instance that shares the same type; or that has a different type until we update it. The second possibility means injective type families wouldn't help much.) So we instead need to write
gist ((defaultConfig @[Bool]) { ... }) [True]
which is no fun. That extra unnecessary-looking set of parentheses is an added kick in the teeth. So we add functions gistF and gistPrecF, which replace the Config a argument with a Config a -> Config a argument and apply it to defaultConfig. So now we write
gistF (\c -> c { ... }) [True]
But we do keep the existing functions around for the final complication. Some things can't be rendered automatically (e.g. functions), but we sometimes want to render them anyway, or data structures containing them. Like a function Bool -> Int that's equivalent to a pair (Int, Int). Sometimes we can use newtypes and maybe coerce for this, but not always, and it might be a pain even if we can.
It turns out we can handle this case. Consider the type
data Gister a where
FnGister :: (Int -> a -> Doc) -> Gister a
ConfGister :: Gist a => Config a -> Gister a
runGisterPrec :: Int -> Gister a -> a -> Doc
runGisterPrec prec = \case
FnGister f -> f prec
ConfGister c -> gistPrec prec c
A Gister is a renderer for any type. For types implementing Gist, we can create a Gister through Config, but for any other type we can still write our own rendering function.
This lets us have an instance Gist [a] without first requiring Gist a. We can't have a (useful) default config in that case, the only fully general Gister as we could write would ignore the value they're passed. But we can still have a default when we do have Gist a (assuming it has its own default):
class Gist a where
type Config a :: Type
type HasDefaultConfig a :: Constraint
defaultConfig :: HasDefaultConfig a => Config a
gistPrec :: Int -> Config a -> a -> Doc
data ConfigList a = ConfigList
{ showFirst :: Maybe Int
, gistElem :: Gister a
}
instance Gist [a] where
type Config [a] = ConfigList a
type HasDefaultConfig [a] = (Gist a, HasDefaultConfig a)
defaultConfig =
ConfigList { showFirst = Nothing, gistElem = defaultConfig }
gistPrec = ...
So now you can call gist on a [Bool -> Int], and you need to write for yourself how to render one of those functions but you can use gist when you do so. There's no defaultConfig @[Bool -> Int], but you can do a type-changing update of defaultConfig @[Void] or similar. Though this is harder than we might like, because we can't derive a Generic instance for Gister a which means we can't use generic-lens or generic-optics. Fine in this case, annoying for nested structures, might be able to improve.
And that's just about everything for this solution.
So this preserves a lot of the good stuff about the classless solution. It's still reasonably simple as Haskell code, at least according to my judgment. We can still render any type, though it would be even simpler if we removed that option. And the user can still completely override the implementer if they want, though not as seamlessly as before.
And it's usually going to be a lot less verbose, with less need to change when your data structure changes. If the bits you've configured haven't changed, you should be good.
But there's still things not to like. For one, the tedious-for-implementers thing hasn't changed.
For another, if a type shows up at multiple places in the data structure, you probably want to render it the same in all of those places; if you have a [(Float, Float)] you probably want to render the fsts the same as the snds. But to do that you have to remember every place it might show up and configure them all separately; and if it starts showing up in a new place, it's probably easy for you to forget to configure that one. (Unlike with the classless solution, where you'll get type errors if you forget about it.)
You're also going to be dealing with nested record updates, which I find unpleasant and have a bunch of questions about. That's somewhat the case with the classless solution too, but I think less deeply nested due to the structure of arguments and the lack of Gister. And here, you'll sometimes be doing type-changing record updates, and I think the future of those is uncertain (they're not supported by OverloadedRecordUpdate).
Implementation for Maybe
data ConfigMaybe a = ConfigMaybe
{ showConstructors :: Bool
, gistElem :: Gister a
}
deriving stock Generic
instance Gist (Maybe a) where
type Config (Maybe a) = ConfigMaybe a
type HasDefaultConfig (Maybe a) = (Gist a, HasDefaultConfig a)
defaultConfig = ConfigMaybe False (ConfGister $ defaultConfig @a)
gistPrec prec (ConfigMaybe {..}) = if showConstructors
then \case
Nothing -> "Nothing"
Just x -> parensIf (prec > 10) $ "Just" <+> runGisterPrec 11 gistElem x
else \case
Nothing -> "_"
Just x -> runGisterPrec prec gistElem x
-- Renders "()". `gist_` is `gistF id`.
gist_ $ Just ()
-- Renders "Just ()".
gistF (\c -> c { showConstructors = True }) $ Just ()
Implementation for GameState
import qualified Gist
import Gist ( Gist(..) )
import qualified Gist as Gist.ConfigList ( ConfigList(..) )
import qualified Gist as Gist.ConfigMaybe ( ConfigMaybe(..) )
deriving via Gist.Showily Player instance Gist Player
deriving via Gist.Showily PieceType instance Gist PieceType
deriving newtype instance Gist (Board a)
data ConfigPiece = ConfigPiece
{ singleChar :: Bool
, gistPieceType :: Gist.Gister PieceType
, gistOwner :: Gist.Gister Player
, gistLastMoved :: Gist.Gister (Maybe Int)
}
deriving stock Generic
instance Gist Piece where
type Config Piece = ConfigPiece
defaultConfig = ConfigPiece False
(Gist.ConfGister $ defaultConfig @PieceType)
(Gist.ConfGister $ defaultConfig @Player)
(Gist.ConfGister $ defaultConfig @(Maybe Int))
gistPrec prec (ConfigPiece {..}) piece@(Piece {..}) = if singleChar
then prettyPieceChar piece
else Gist.record
prec
(Just "Piece")
[ ("pieceType", Gist.runGister gistPieceType pieceType)
, ("owner" , Gist.runGister gistOwner owner)
, ("lastMoved", Gist.runGister gistLastMoved lastMoved)
]
data ConfigGameState = ConfigGameState
{ gistTurn :: Gist.Gister Player
, gistPBlackWin :: Gist.Gister Float
, gistPWhiteWin :: Gist.Gister Float
, gistNMoves :: Gist.Gister Int
, gistBoard :: Gist.Gister (Board (Maybe Piece))
}
deriving stock Generic
instance Gist GameState where
type Config GameState = ConfigGameState
defaultConfig = ConfigGameState
{ gistTurn = Gist.defaultConfGister
, gistPBlackWin = Gist.defaultConfGister
, gistPWhiteWin = Gist.defaultConfGister
, gistNMoves = Gist.defaultConfGister
, gistBoard =
let
gPiece = Gist.defaultConfGisterF $ \c -> c { singleChar = True }
gMPiece = Gist.defaultConfGisterF
$ \c -> c { Gist.ConfigMaybe.gistElem = gPiece }
gLMPiece = Gist.defaultConfGisterF
$ \c -> c { Gist.ConfigList.gistElem = gMPiece }
gBoard = Gist.defaultConfGisterF
$ \c -> c { Gist.ConfigList.gistElem = gLMPiece }
in
gBoard
}
gistPrec prec (ConfigGameState {..}) (GameState {..}) = Gist.record
prec
(Just "GameState")
[ ("turn" , Gist.runGister gistTurn turn)
, ("pBlackWin", Gist.runGister gistPBlackWin pBlackWin)
, ("pWhiteWin", Gist.runGister gistPWhiteWin pWhiteWin)
, ("nMoves" , Gist.runGister gistNMoves nMoves)
, ("board" , Gist.runGister gistBoard board)
]
-- Renders in short form. `gist_` is `gistF id`.
gist_ startPos
-- Renders in long form. This uses generic-lens to do record updates, but an
-- approach like used in `defaultConfig` would work too:
-- gistF (let ... in \c -> c { gistBoard = gBoard }) startPos
gistF
( setField @"gistBoard"
$ Gist.defaultConfGisterF
$ setField @"gistElem"
$ Gist.defaultConfGisterF
$ setField @"gistElem"
$ Gist.defaultConfGisterF
$ setField @"gistElem"
$ Gist.defaultConfGisterF
$ setField @"singleChar" False
)
startPos
-- Renders in fully explicit form. This could also be done with standard record
-- updates.
gistF
( setField @"gistBoard"
$ Gist.defaultConfGisterF
$ setField @"gistElem"
$ Gist.defaultConfGisterF
$ setField @"gistElem"
$ Gist.defaultConfGisterF
$ ( setField @"showConstructors" True
. ( setField @"gistElem"
$ Gist.defaultConfGisterF
$ ( setField @"singleChar" False
. ( setField @"gistLastMoved"
$ Gist.defaultConfGisterF
$ setField @"showConstructors" True
)
)
)
)
)
startPos
Two-class solution
So here's a very different approach.
First, we find some way to store the config for every possible in a single data structure, even though we don't know all the possible configs yet.
Then we make this config store available to renderers. They look up the config that's relevant specifically to them. When rendering their contents, they simply pass down the same config store. A MonadReader helps here.
This makes "update the config of every occurrence of a type" easy. It makes "update the config of just this specific occurrence of a type" impossible. So we also track our location in the data structure, and in the config store we let users say "this option only applies at this location", or "at locations matching …".
(This last bit sounds almost more trouble than it's worth. But without it, it becomes super awkward to handle things like "only show three levels deep of this self-referential data type".)
This is currently implemented in the Gist.TwoClass module. There's also a Gist.Dynamic module which has just the config-data-structure part, and is actually the implementation I've fleshed out the most. But I currently think it's not worth exploring more and not worth discussing in depth by itself.
Somewhat simplified, here's the main stuff going on with this solution:
-- | Opaque storage of config options, implemented with existential types. Not
-- type-safe by construction, but has a type-safe interface.
newtype Config = UnsafeConfig { ... }
-- | Things that can be put into a `Config`.
class (Typeable a, Monoid (ConfigFor a), Typeable (ConfigFor a))
=> Configurable a
where
type ConfigFor a :: Type
-- | Tracking and matching locations in the data structure.
newtype GistPath = ...
data PathMatcher = ...
data GistContext = GistContext
{ gcPath :: GistPath
, gcConf :: Config
}
-- | Things that can be rendered.
class Configurable a => Gist a where
renderM :: MonadReader GistContext m => Int -> a -> m Doc
-- | The user-facing interface.
gist :: Gist a => [Config] -> a -> Doc
config :: Configurable a => Maybe PathMatcher -> ConfigFor a -> Config
The separation between Configurable and Gist might seem unnecessary here - why would we configure something we can't render? The answer is that Configurable doesn't specify the kind of its argument. So we have all of
instance Configurable Map
instance Typeable k => Configurable (Map k)
instance (Typeable k, Typeable v) => Configurable (Map k v)
and then users can add configuration for all Maps without needing to specify the exact types. (And they can override that config at specific types, if they want, using the Semigroup instance of the ConfigFor.) We also have instance Configurable Floating, and then the Gist instances for both Float and Double can look that up.
So the flow is that users build up a Config data structure, specifying "for this type, (optionally: at this location in the data structure,) set these options".
Then we walk through the structure. At each point we look up the relevant config values for the type at the current location, and possibly for other types, and combine all these in some way that users will just have to beat into submission if they're doing something complicated. And then we render, passing an updated GistPath and the same Config to any subcomponents.
This isn't very transparent to users. The Float instance looks up config for both Float and Floating, and the Maybe a instance looks it up for both Maybe a and Maybe. But to discover these you have to either try it and see, or look at the source code, or read the instance docs that someone probably forgot to write.
Also, each config option needs to have a Monoid instance that distinguishes between "this value hasn't been set" and "this value has been set to its default". In practice that means Last. But that means users don't know what the default value of any config option is.
So the actual code complexifies the implementation in a few ways, to help users. Instances have a way of specifying "these are the types I look up", as long as those types have the same ConfigFor. Then looking things up from the config happens automatically; and there's a separate function to set default values to what gets looked up, which users can call manually to see what's going on. Once we have the defaults we no longer need Last, so we change to Identity at that point.
We also use a custom monad class instead of MonadReader GistContext. For now it's no more powerful, but it would be easy to add a tracing function. Then if users had trouble figuring out what was going on, they could use that to help figure it out, with no additional work from implementers.
So the actual implementation looks more like
class (Typeable a, Monoid (ConfigFor a Last), Typeable (ConfigFor a Last))
=> Configurable a
where
type ConfigFor a (f :: Type -> Type) :: Type
class (Configurable a, CanDoLookups (GistLookups a) (ConfigFor a Last))
=> Gist a
where
type GistLookups a
reifyConfig :: ConfigFor a Last -> ConfigFor a Identity
renderM :: MonadGist m => Int -> ConfigFor a Identity -> a -> m Doc
config :: Configurable a => Maybe PathMatcher -> ConfigFor a Last -> Config
where CanDoLookups roughly ensures that GistLookups a is a type-level list of things with a given ConfigFor. (But we can't use '[] for these type-level lists, because you can't put types of different kinds inside one of those.)
How does this fare? The big advantage over the previous solutions is the "configure every occurence of a type at once" thing. I anticipate this is usually what users want, so it's good that it's easy. Also, no nested records! And if I decide to add global config options - perhaps indent width - I just need to add them to GistContext.
I think the big downsides are that it's wildly complicated, and we've lost the ability to render anything we can't write a Gist instance for (which also means users can't override implementers' decisions). But also a bunch of other downsides. When you do want to render different occurrences of the same type differently, it's awkward. You won't get errors or warnings if your config gets out of sync with the type you're rendering. Encapsulation is tricky, internals of your types might be exposed in ways you don't want. It's not necessarily clear how you'd want newtypes to be configured, and newtype-deriving only gives you one option which might not be what you want.
Implementation for Maybe
data ConfigMaybe f = ConfigMaybe { showConstructors :: f Bool }
deriving stock Generic
instance Semigroup (ConfigMaybe Last) where
a <> b = ConfigMaybe (showConstructors a <> showConstructors b)
instance Monoid (ConfigMaybe Last) where
mempty = ConfigMaybe mempty
instance Configurable Maybe where
type ConfigFor Maybe f = ConfigMaybe f
instance Typeable a => Configurable (Maybe a) where
type ConfigFor (Maybe a) f = ConfigFor Maybe f
instance Gist a => Gist (Maybe a) where
type GistLookups (Maybe a) = CL Maybe
reifyConfig (ConfigMaybe {..}) =
ConfigMaybe (Identity $ fromLast False showConstructors)
renderM prec (ConfigMaybe {..}) = if runIdentity showConstructors
then \case
Nothing -> pure "Nothing"
Just x -> do
renderedElem <- subGistPrec 11 Nothing x
pure $ parensIfPrecGT 10 prec $ "Just" <+> renderedElem
else \case
Nothing -> pure "_"
Just x -> subGistPrec prec Nothing x
-- Renders "()".
gist [] $ Just ()
-- Renders "Just ()".
gist [configF @Maybe $ \c -> c { showConstructors = pure True }] $ Just ()
Implementation for GameState
import qualified Gist
import Gist ( Configurable(..), Gist(..), fromLast )
import qualified Gist as Gist.ConfigMaybe ( ConfigMaybe(..) )
deriving via Gist.Showily Player instance Configurable Player
deriving via Gist.Showily Player instance Gist Player
deriving via Gist.Showily PieceType instance Configurable PieceType
deriving via Gist.Showily PieceType instance Gist PieceType
-- We can't derive an instance `Configurable Board`. We have that `Board a` is
-- representation-equivalent to `[[a]]`, but `Board` itself isn't
-- representation-equivalent to anything. Anyway, even if we had an instance,
-- the instance we're deriving for `Gist (Board a)` wouldn't look at it.
deriving newtype instance Typeable a => Configurable (Board a)
deriving newtype instance Gist a => Gist (Board a)
data ConfigPiece f = ConfigPiece { singleChar :: f Bool }
deriving stock Generic
instance Semigroup (ConfigPiece Last) where
(ConfigPiece a1) <> (ConfigPiece a2) = ConfigPiece (a1 <> a2)
instance Monoid (ConfigPiece Last) where
mempty = ConfigPiece mempty
instance Configurable Piece where
type ConfigFor Piece f = ConfigPiece f
instance Gist Piece where
type GistLookups Piece = ()
reifyConfig (ConfigPiece a) = ConfigPiece (Identity $ fromLast False a)
renderM prec (ConfigPiece {..}) piece@(Piece {..}) =
if runIdentity singleChar
then pure $ prettyPieceChar piece
else Gist.record
prec
(Just "Piece")
[ ("pieceType", Gist.subGist (Just "pieceType") pieceType)
, ("owner" , Gist.subGist (Just "owner") owner)
, ("lastMoved", Gist.subGist (Just "lastMoved") lastMoved)
]
instance Configurable GameState where
type ConfigFor GameState f = Proxy f
instance Gist GameState where
type GistLookups GameState = ()
reifyConfig _ = Proxy
renderM prec _ (GameState {..}) =
Gist.localPushConf
(Gist.configF @Piece $ \c -> c { singleChar = pure True })
$ Gist.record
prec
(Just "GameState")
[ ("turn" , Gist.subGist (Just "turn") turn)
, ("pBlackWin", Gist.subGist (Just "pBlackWin") pBlackWin)
, ("pWhiteWin", Gist.subGist (Just "pWhiteWin") pWhiteWin)
, ("nMoves" , Gist.subGist (Just "nMoves") nMoves)
, ("board" , Gist.subGist (Just "board") board)
]
-- Renders in short form.
gist [] startPos
-- Renders in long form. generic-lens could replace the record update, one of:
-- configF @Piece $ setField @"singleChar" $ pure False
-- configF @Piece $ field @"singleChar" .~ pure False
gist [Gist.configF @Piece $ \c -> c { singleChar = pure False }]
startPos
-- Renders in fully explicit form. generic-lens would work here too, avoiding
-- the horrible import.
gist
[ Gist.configF @Piece $ \c -> c { singleChar = pure False }
, Gist.configF @Maybe
$ \c -> c { Gist.ConfigMaybe.showConstructors = pure True }
]
startPos
I've given three different renders for all of these GameState examples. "Short form" looks like the example I gave above, except I haven't configured the floats to show as percentages. (Like I said, not yet implemented.) "Fully explicit form" is similar to the pretty-simple rendering, except with a different indent style. And "long form" is in between, with abbreviated rendering for Maybe but everything else displayed in full - there's no ambiguity here, so it seems like a good choice even if you don't want any data missing.
In this particular case, rendering GameState for the classless and one-class solutions are about as verbose as each other. I think that's kind of a coincidence based on where the type variables are and what we're doing with them. For example, GameState has no type variables, so its renderers can be passed in ConfigGameState, letting them be defaulted. Board has a type variable, but renderBoard has no other config options; so there are no cases where with one-class we can say "change this option for how we render Board, but leave the sub-renderer alone", but with classless we can only say "change this option for how we render Board, and while we're at it here's the sub-renderer to use". This kind of thing does come up once, when in the fully-explicit form we want to set showConstructors on the lastMoved renderer, and have to also repeat the renderer for the Int. But in that case the renderer is just gistShowily so it doesn't hurt much.
I expect there'd be more difference in other cases. But maybe I'm wrong? Who knows.
A thing I dislike in all of them, is how I've had to do imports to handle record field updates. As of (I think) GHC 9.2, record updates combined with DuplicateRecordFields is more awkward than it used to be, at least if you don't want to get warnings about future compatibility. So when I do the awful
import qualified Gist as Gist.ConfigMaybe ( ConfigMaybe(..) )
that's so I can do val { Gist.ConfigMaybe.showConstructors = ... } to update the field. Another option is to use generic-lens or generic-optics to do updates, which I've also demonstrated in some cases. My guess is that would be fine in a lot of application code, but many libraries won't want to depend on them.
I could also try to choose constructor names not to conflict. But I think that basically means prefixing them all, which would also be super verbose, and it would annoy users of the generic libraries.
(Given what I've implemented so far, the name conflicts only actually exist in the one-class solution, which reuses the name gistElem. But I expect showConstructors and showFirst to also get reused, e.g. for gisting Either and Set; and something like countRemaining could be useful for collections that get truncated, and so on. So it seemed more useful to write things this way.)
I haven't looked closely, but anonymous records might help here. They also might help with Generic-based defaulting, which is another thing I haven't looked into. But they seem like a large hammer that increases dependency footprints. And from a quick look I'm not sure they support type-changing record updates.
I'd prefer if there wasn't a single fixed indent style. But I'm not sure what to do about it. Conceivably, I could have a fixed IndentStyle type, and expect implementers to pay attention to it. (Similar to how precedence has been granted special status.) But I expect if I do that, there'll be situations where people wish the type was larger (because it doesn't support things they want), and others where they wish it was smaller (because implementing support for all the options is a pain). If I make it maximally small, we only have one of those problems. Similar thoughts on possible color support.
Questions for you
One reason I wrote all this is to try to gauge enthusiasm. One possible future for pretty-gist is that I use it a small amount and in personal projects and at my job, and basically no one else uses it at all. That would be fine.
Another possible future is that it becomes a package that other people do use and that I take responsibility for. But that's only going to happen if it seems like anyone cares.
So some things I'd like to know from readers:
- How cool do you think each version is?
- How likely are you to use each version?
- How annoyed would you be, for each version, if you felt obligated to implement support for it for a library you maintain or similar?
- Which version do you think is coolest / are you most likely to use / least likely to be annoyed by?
- Do you see ways to improve any of them without significant costs?
- Do any of them seem to have significant advantages or disadvantages I missed?
- What would you use them for?
- Can you think of other approaches to solving this problem that you think you might like better than any of these?
I have some opinions on these myself, but I'd prefer to wait and see what others say before revealing. I also have another possible approach vaguely in mind; but if I waited to explore it before publishing, then this would never get finished.
The canonical public place to leave comments is the reddit thread. But I've also set up a google form you can fill in if you prefer.
Posted on 10 August 2023
|
Comments
According to Wikipedia, the Shard (the tallest building in the UK) stands "309.6 meters (1,016 feet) high". I put this in my Anki deck as "Height of the Shard / 310m", but I was saying "height" to mean "tallness" (because I don't much like that word) and I had assumed Wikipedia was using it the same way. So I thought the Shard was 310 m tall.
But according to Bron Maher in Londonist,
most sources put the building’s tallness - that is, its length base-to-tip - at about 306 metres. The last three metres come from the height of the ground on which the Shard is built. So while its height is indeed 309 metres above sea level, the Shard is only 306 metres tall.
Is that so? I was curious enough to investigate, but it turns out I don't really know how to.
(Also: Maher says the Shard is 306 m, not 309 m, not "not 310 m". And he gets 309 from Wikipedia, quoting it on the list of highest points in London, which talks about "the 309 m (1,014 ft) tall Shard". Where did those extra 60 cm go? The article on the Shard itself also has that number, in the "records" section near the bottom, but the infobox on the right has 309.6/1,016. So is it 306 m, 309 m, or 309.6 m?)
The boring investigation
The first thing to do is to look at Wikipedia's sources. It doesn't have one on the list of highest points, and it doesn't have one in the "records" section. The infobox does have a source for the height, which is on skyscraperpage.com. It lists the spire at 1,016 ft or 309.7 m, yet another number! There are various drawings, all giving the roof at 304.2 m and the spire at 309.7 m. (1,016 ft is 309.68 m, but 309.6 m is 1015.75 ft and 309.7 m is 1,016.08 ft. So if you convert 309.6 m to feet and back to meters, you could get 309.7 m. But wikipedia shouldn't be taking 309.6 m from that page.)
Skyscraperpage lists the source for the height as http://www.the-shard.com, and the about page on that site says: "How tall is The Shard? The Shard is 309.6 metres, or 1,016 feet, high and is Western Europe's tallest building." You'd certainly expect the Shard's official webpage to be right about this, but also it says "high" not "tall" so it could be a misdirect.
Next, does Maher have any sources? For 306 m tallness he just says "most sources" give that figure. For 3 m above sea level, I think that comes from its height at the top. He quotes someone at Ordnance Survey saying the top of the Shard is 308.9 m above sea level, which gives around 3 m for the base.
Most of my research was just googling things. Search terms included "how tall is the shard", "height above sea level of the shard", "the shard architectural drawings", "uk contour lines" and "ctbuh the shard" (inspired by one of the earlier results). Here are some of the things I found.
The London Pass: "The Shard is 306 metres tall, however if you measure all the way up to the tip, it's 310 metres". I don't know what point below the tip it's talking about. It could be roof versus spire, but the skyscraperpage drawings give a different roof height.
The Skyscraper Center: height ("measured from the level of the lowest, significant, open-air, pedestrian entrance") is "306 m / 1,004 ft", both "to tip" and "architectural". (The difference being things like flagpoles and antennae, which the Shard doesn't have. The highest occupied floor is "244.3 m / 802 ft".) Seems like the kind of site that knows what it's talking about. Doesn't cite sources, but the drawing they have is labeled a CTBUH drawing, and that also sounds like the kind of organization that knows what it's talking about, giving me a new google search term.
SkyscraperCity: says both "309m" and "310m" with no apparent shame. But also, that link points to page 833 of 1385 of a discussion thread, and at this particular point people are discussing its height above sea level. (And comparing to the then-future "The Pinnacle", which became 22 Bishopsgate.) It seems the Shard is level with The Thames nearby, which at that point is tidal. Some commenters think that means it's at sea level at least some of the time, but someone else points out no: "A river can be tidal some distance above high water mark for the sea. Consider what happens when the tide comes in - the sea effectively "comes up" the river mouth, which will slow down flow of water down the river, which will start backing up. As it backs up, the level upstream will increase as less water is getting out. Thus a river can be tidal above the high tide point of the sea itself." Makes sense to me.
Someone else says it's 16 m above sea level according to Google Maps, but I can't find that info on Google Maps myself. (But it does label it as "306m-high glass & steel tower with views", if I'm zoomed in the right amount. I can't see that string anywhere else.)
Another says it's 16 m above sea level, according to "the Ordinance Datum figures". Presumably they mean Ordnance Datum; that's not a source, their point is to talk about "what is the zero-point that this is 16 m above". (In different comments they say 16 or 17 m, but I'm pretty sure they mean 16.)
On the next page, someone links to a nearby ordnance survey benchmark which seemingly puts the ground there at 4.563 m above sea level. (But we get 3dp precision for the height of the mark above sea level, and only 1dp precision for its height above ground level, which is sus. Probably best stick to 4.5 m above sea level, and then the Shard would be somewhat close to that - unless there are steps or a steep hill in between, and I'm sure there are some nearby.) (The benchmarks site doesn't have an FAQ entry for "what actually are these things we've catalogued so painstakingly", so here's Ordnance Survey explaining them. I think "cut mark" just means "we marked the location by making a cut in the wall somewhere".)
Someone else on the next page says Bing Maps has an Ordnance Survey overlay. Looking at that: the Shard is contained in a fairly small contour line, but that line isn't marked with a height. The next-nearest contour I can find is marked 10 (which is in meters), so this one could be either 5 or 15, making both 16 m and "somewhat close to 4.5 m" plausible, which is frankly ridiculous.
There's this topographic map. It doesn't have the Shard actually labeled, but clicking various points inside its outline I can get between 15 and 20 m. I don't think there's actually a 4-6 m difference between different corners of the base of the Shard, so this seems unreliable. And points near the benchmark seem to be about 12-15 m. It's plausibly using a different zero point than Ordnance Survey?
I couldn't find any more topographic data for free. This site might help, but I'd need to register for an account and I'm not sure that would be enough.
This pdf hosted on the CTBUH domain says 310 m height. There's also this pdf which doesn't give a height, but does have a ground configuration table; we have "made ground" from +4.7 m OD to 0.0 m OD, matching the OS benchmark. Other pdfs in the search result say 306 m, 306 m, and 1,016 ft / 310 m.
Wikiarquitecture: 310 m.
This drawing: 306 m.
And that's it for googling.
Oh! This is kind of embarrassing to admit, but even though I go by the Shard pretty often I don't have a good sense of the road layout near it, or indeed which building in the road layout is the Shard. (When you're next to it and not looking up, it's much like any other building.) But scrolling around street view for a bit to refresh my memory, I realize it has ground-level exits on at least two different floors, with an outside escalator that's probably something around 10 m elevation. (On screen it's about 4.5x the height of that guy, so I'd guess a bit under. And I think I count 36 escalator steps, this says typical escalator step rise is 8 1/2 in, which makes 7.77 m.) There's also a pedestrian walkway going underneath the level of the upper street, but that's too wide to think of as a bridge. So actually, a 4-6 m difference between corners is totally reasonable; what counts as "ground level" when you're inside a building like that? Still, the topographic map disagrees with OS about the benchmark too.
I searched HM Land Registry for the Shard, but the results don't give me anything interesting. It was a long shot.
And my final source is the aviation charts for nearby London City Airport. (Thanks to Tobias at Zurihac who suggested these and showed me where to find them.) They're on this site which doesn't like direct linking, so you have to go to "Part 3 - Aerodromes" -> "AD 2 Aerodromes" -> "EGLC London City" -> "EGLC AD 2.24 charts related to an aerodrome" -> "Control zone and control area chart", and that gives you this pdf. The Shard isn't named, but there's something there with height marked as "1015 (1008)" in its rough location, so let's assume it's that. This is presumably in feet, and Tobias thinks the 1008 is height above ground. This matches what is presumably the Crystal Palace transmitter south and slightly east, at "1087 (732)", or "331 (223)" in metres, which is close to Maher's figures for it. (Maher has it 222 m above the ground, but I'm not investigating that.) So in metres this is 309.4 (307.2), but since that's rounded it could be 309.2-309.5 (307.1-307.4).
The exciting conclusion
So… I'm not sure, really. I think my best guess is that it's 306 m tall according to some perfectly reasonable way to measure that, possibly the most reasonable. This is consistent with (i.e. lower than) the heights given by both OS and the aviation charts, and those are close enough that the difference might be caused by differing ideas of sea level. And it's the only number I remember seeing lower than those, other than the aviation charts.
If this is right then it's about 3 m above sea level at the ground, which is close enough to the benchmark height that I can believe it. I don't think I believe the "16 m above sea level" value; even a combination of "confused about which street level we're measuring from" and "differing ideas of sea level" seems like it couldn't give that. I also don't think I believe the 4.7 m from the ground configuration table - that table suggests that before development, the ground there was within 5 cm of sea level, and in particular below the nearby Thames most or all of the time. Not inconceivable, but in context I doubt.
This makes the aviation charts wrong about its tallness, which is my biggest sticking point here. But I'm not sure how reliable to expect them to be about that. Height seems far more relevant to their interests than tallness, and they could easily be using a ground-height measurement at some nearby point.
I think the funniest way to resolve this for good, would be for someone to announce plans for a 307 m tall building with its base 4 m above sea level, and specifically claim it as taller than the Shard. The skyscraper fandom will presumably erupt into civil war, but when the dust settles we can hope they'll have uncovered the truth.
Why is this answer so hard to find? It feels like the sort of question that has a single definite answer that you can just look up, but clearly not.
It's probably relevant that I can't easily check for myself. I suppose I could use a sextant or look at shadow lengths. But those will both work best if I'm far away, and then other buildings make it harder plus I might no longer be at ground level. I don't think I can even get to the top, let alone dangle a tape measure from it. I think GPS gives me height above sea level, but I'm not sure how precise it is, how accurate it is (especially when surrounded by buildings), and again I can't go to the top. So if two sources disagree, there's no obvious way for me (or probably most people) to check which if either is correct. But why do sources disagree in the first place?
Sometimes with tall buildings the issue is that there are multiple things that could be considered "the top". Two sources suggest that might be happening here. But they still disagree, and the Skyscraper Center suggests it's not.
Might it be that different sources define sea level differently? Perhaps, but this isn't enough by itself unless someone used different sea levels for the top and the bottom. I'm not sure how much difference we can expect this to explain.
How about forgetting the difference between height and tallness? This does seem plausible to me. I could imagine someone standing at the top of the Shard with a device telling them they're (say) 309.6 m above sea level, and forgetting to also use that device on the ground. It seems to roughly fit, but not closely enough to be conclusive and of course none of the numbers are sourced well enough for this error to be detectable in the methodology.
I could then imagine those two heights getting rounded to 309 m and 310 m respectively; or 309.6 m getting truncated to 309 m; or 306 m tallness getting rounded to 310 m; and that could explain some of the numbers I see. Converting meters to feet and back can also generate new numbers.
It's also possible that different sources are counting from different bottoms. I don't think there's a street-level entrance that would get us above 306 m, but maybe including a basement.
I wonder if plans changed during construction, reducing the intended tallness? But I can't find any evidence of that.
This article on building the Shard points out that buildings shorten during construction. It sounds like that was accounted for, but plausibly a pre-shrinking height somehow got mistaken for the finished height? (It also has a picture which makes me think that the difference between "highest floor" and "actual tip" is at least 20 m.)
And I can't rule out measurement error, either. I don't know how OS decided the tip was 308.9 m above sea level, or the aviation charts people decided it was 1,015 ft, but while I consider them fairly reliable-seeming organizations, it sure seems possible that someone misread or miscalibrated an instrument.
But ultimately I don't have a satisfying answer here, either.
Posted on 23 June 2023
|
Comments
I've heard that descaling a kettle makes it more efficient, and can save me time and money.
Okay, but how much? For some reason my my intuition says it'll be basically unnoticable. Let's try to figure it out, and then actually try it.
The Models
There's a first-order approximation which says this should be impossible: heating things up is 100% efficient. What's the limescale going to do, convert some electricity into forms of energy other than heat?
No, but it might cause the heat to go to the wrong places. I think there are two ways that could happen. The first is if the limescale itself has a high heat capacity, meaning it takes a lot of energy to heat up. That doesn't seem likely to me; I think there's likely less than 10 g of it, and I think it probably has less heat capacity than the same mass of water (because I think water's is higher than most other things). I don't think adding 10 ml water (weighing 10 g) to my kettle will significantly effect the boiling time.
Spot check: water's specific heat capacity is about 4 J/K·g. So to heat 10 g water by 100 K needs about 4000 J. My kettle is 2200 W according to the email I got when I bought it, so an extra 10 ml should take about 2 s longer to boil.
Also, I normally boil about 500 ml of water, so we'd expect 10 ml extra to make about a 2% difference. (I don't have a strong intuition for how long my kettle normally takes to boil. 1-3 minutes? The above calculation suggests it should be around 100 s.)
The second way the limescale could matter is if it's a good thermal insulator. Then the metal heating element gets significantly above 100°C before the water boils. And from my googling, it seems like this is the reason people give that descaling a kettle is helpful. How much effect would this have?
This page says the thermal conductivity is 2.2 W/m·K. I don't remember studying this in school, and I don't find that wikipedia page very clear. But I think maybe this means: the rate of energy transfer (W) from the heating element is 2.2 W/m·K, multiplied by the surface area of the heating element (m²), divided by the thickness of the limescale (m), multiplied by the temperature difference (K) between the heating element and the water. The units check out at least.
This implies, if there's no limescale, that the power transfer should be infinite, regardless of the size of the heating element. That's clearly not how things work. Still, it seems fine to have as a model, it just means that the water and heating element will stay the same temperature.
But doing some field research (i.e. looking at my kettle) makes me think it's a bad model in this case. Here's what it looks like:

(This kettle was last descaled around August 2020. I know because I bought vinegar for it, and thanks to online shopping the receipt is in my email.)
It seems that I have some limescale over some of the heating element (bits of the metal plate at the bottom, and the tube around where it passes through the plate), and zero limescale over some of it. The "no limescale gives ∞ W/K" model is going to give ∞ W/K no matter how small the no-limescale area is. So scratch that model.
I don't feel like trying to model the rate of power transfer from an un-limescaled heating element to water. I don't know what material it's made of (some kind of steel I suppose?), and I don't know what property of that material to look up. Plus it probably depends on how fast water convects.
Here's another way to think about it: assume that the amount of metal the manufacturer used is roughly as small as possible without compromising too much on boiling speed.
When we turn the kettle on, we start putting 2200 W into the heating element, and the heating element starts putting some of that into the water. When the heating element is sufficiently hot, it can pour 2200 W into the water, and we're at 100% efficiency.
(Except that as it heats up the water, it needs to get hotter itself to maintain that 2200 W rate. So we'll never actually be putting 2200 W into the water. But I'm gonna guess that we can ignore this effect for current purposes. Also, if the heating element has enough thermal mass, we might boil the kettle before it gets hot enough to pour 2200 W into the water. I'm gonna guess this isn't the case.)
Energy used to heat the heating element is essentially wasted. I don't know if other kettle designs could do away with one entirely, but as long as we have a heating element there's going to be some wastage. We can minimize the wastage by having the heating element be low-volume (so not much energy needed to heat it) but high surface area (so high rate of energy transfer to the water).
If the rate of energy transfer is 1 W/K, then we reach 100% efficiency when the heating element is 2200 K hotter than the water. But long before you reach that point you're going to melt the plastic of the kettle, which would be bad. (The highest melting temperature of any plastic listed on this page is 390°C.)
If it's 10 W/K, then we reach 100% efficiency at 220 K hotter than the water. Some plastics can survive 320°C, but idk, it still seems bad.
But at 100 W/K, we only need to get 22 K hotter than the water. That seems like it should be fine?
Let's assume that under optimal conditions, the heating element reaches $x$ K hotter than the water. That suggests the rate of energy transfer is $2200/x$ W/K.
Now suppose that some fraction $f$ of the heating element is covered in limescale, and that the rate of energy transfer through the limescale is essentially 0 W/K. Then the heating element will instead reach $x/f$ K hotter than the water. The energy needed to heat it that extra $x{1 - f \over f}$ K, is extra energy wasted.
…but I actually expect the energy needed to heat the heating element to be pretty low? According to this page the specific heat capacity of steels tends to be about 0.5 J/K·g. If the heating element is 100 g of steel, and we heat it an extra 50 K, we waste an extra 2500 J which costs us a bit over a second.
So I'm not super confident in this, but: I don't have a model which suggests descaling a kettle (similar to mine) will have particularly noticeable effects. If it gets sufficiently scaled it'll self-destruct, but I expect this to be very rare. (I don't have a model for how much scaling it takes to reach that point, it's just that I don't remember ever hearing a friend, family member or reddit commenter say they destroyed their kettle by not descaling.)
The Setup
It's almost time for some empiricism! I'm going to see how quickly my kettle boils currently (average of three observations), then I'm going to descale it, and then I'm going to see how quickly it boils after that.
My immediate temptation is to boil a large amount of water, so that the effect is most noticeable. A 10% difference is easier to notice if it's going from 500 s to 550 s, than from 100 s to 110 s. But my models (such as they are) predict that scale decreases initial efficiency but not eventual efficiency; it would be a fixed cost, not a percent cost. And a 10s difference is easier to notice if it's going from 100 s to 110 s, than from 500 s to 510 s.
I don't trust my models, so I'm going to try both small and large amounts. For small amounts, I'm going to fill the kettle to the "2 cup" line. I'm in the UK so that ought to be 568 ml, but most of my mugs are only 500 ml and it's not quite enough to fill one of them. Checking in a measuring jug, it's somewhere between 450 and 500 ml, so likely a US pint, 473 ml. There's some noise here because the kettle has a wide diameter, so we only get small differences in the water level for the volume poured in. My rough guess without measuring is a 5 ml difference between runs is plausible. For large amounts, I'm just going to empty my entire 1.5 l bottle of fridge-water into the kettle. There's some noise here because the bottle doesn't have markings at all and I don't bother to fill it right to the brim, but I do try to get it to roughly the same place. A 5 ml difference between runs seems plausible here too.
I'll use water from the fridge, to mostly control for initial temperature (my guess is it'll start around 3°C). I'm not going to bother trying to control for room temperature or for where in the fridge I keep the water or what phase of the cooling cycle the fridge is in at the time. I'm going to assume that the kettle cuts off when all the water is at 100°C. I'll only measure the first boil of the day, and that way the kettle has definitely had time to cool down overnight. (In hindsight:) I didn't control for whether the kettle had had water sitting in it overnight; that could plausibly make the heating element a few degrees below room temperature.
There's one more calculation to do first, and that's to figure out how quickly it would boil assuming no energy wasted. Then I can make some predictions; do the pre-descaling boils; possibly adjust my predictions; descale; do the post-descaling boils; and compare.
But I'm writing this post out of order, and I've already got the numbers for pre-descaling, without having calculated the maximum efficiency and made predictions based on that. I could make predictions knowing the numbers but not having calculated max efficiency, that seems mostly fine, except that rereading through this I saw that I did do a rough calculation above.
The Prediction
Still, for what it's worth: my current guess is indeed that the effect will be pretty similar in absolute time for both small and large boils; and less than a 10s difference in both cases.
So, is that worth it? In terms of money, obviously not. I don't remember how much I pay for electricity, but it's less than £0.50/kWh. Multiplied by 2.2 kW for 10 s gives about £0.003, I'll save less than £3/year. Definitely not worth paying attention to that kind of money, which is what I expected. (It's even less when you consider the cost of the water and electricity and vinegar I use to descale.)
As for the time… ten seconds isn't much, but the time cost of boiling a kettle isn't how long it takes to boil. It's how long it takes to fill and turn on, plus how long I wait for it after I'm ready for boiling water. (That depends a lot on what I'm making. When I boil it for food, it usually finishes before I'm ready for it, but when I boil it for tea I usually have to wait.) Knocking ten seconds off the waiting could make it more pleasant to use, even if the actual time saving is minimal. I don't think I particularly expect to notice a difference, especially because 10s is the upper range of my prediction, but I won't be shocked if I do. I'm not going to give a numeric probability because I don't want my subjective judgment to be influenced by how it affects my predictive score.
(We don't get to count "time spent writing this post" against descaling. I'm not writing it to save myself time, I'm writing it to practice my sience skills and have fun doing so.)
Okay, actual calculations: we're making a 97 K difference in water temperature. The specific heat capacity is 4.184 J/K·g, and the density is 1 g/ml. The power transfer at 100% efficiency is 2200 W. So for $x$ ml of water, we need a minimum of ${97 · 4.184 \over 2200} x$ s to boil. For 473 ml that's 87.3 s, and for 1500 ml that's 276.7 s.
If you want to make some predictions before you see the actual times, here's some space for you to do so.
…
…
…
…
…
The results
The actual pre-descaling times: for small I measured 103, 105 and 107 s, average 105. That's 17.7 s or 20% higher than theoretical minimum. For large I measured 296, 290 and 300 s, average 295.3. That's 18.7 s or 7% higher than minimum.
I think this is looking pretty good for the "initial efficency, not eventual efficiency" models. I still expect descaling to make less than a 10 s difference in both.
If you want to change your predictions, here's some space for that.
…
…
…
…
…
I had to descale twice, the first time I don't think I put in enough vinegar relative to water. Here's what it looked like after the second attempt:

Now I measured 103, 104 and 104 s for small, average 103.7, 1.3 s faster than before. And 298, 296, 293 s for large, average 295.7, 0.3 s slower than before.
I assume these results aren't statistically significant, and I'm sure they're not practically significant. Descaling my kettle basically just doesn't speed it up unless it's much more scaly than it was this time. You know your kettle better than I do, but my guess is it won't speed up yours either. Don't be fooled by big vinegar.
I should have given a numeric probability for "no detectable difference". (The probability I was reluctant to give was for "I notice a difference when I'm not measuring".) Thinking back, I think that just before descaling I would have given this… something like 30-50% probability?
The caveats
There may be other reasons to descale your kettle. Some friends mentioned flavor; I don't remember hearing that as a reason before, and I didn't notice a difference, but I'm the opposite of a supertaster. One mentioned getting scum on top of tea when a kettle is too scaly; I haven't noticed that either, but I'm probably also the opposite of a super-scum-noticer.
Also, my partner pointed out that post-descaling, the 2-cup mark holds slightly more water than it used to. I think this is less than the uncertainty in my measurements anyway, and in practice I use those markings to decide how much to fill my kettle so maybe it's correct not to control for this effect. Still, I'm a little embarrassed I didn't think of it in advance.
Update: Shortly after this, I semi-accidentally descaled my kettle's filter, which is something it hadn't occured to me to do. It pours so much more easily now! It used to be that if it was more than about half full it would drip water down the spout when I tried to pour it, but it doesn't do that any more. 10/10, will descale the filter again, even if not the heating element.
Posted on 02 May 2023
|
Comments
t ≈ 0s
I am born into knowledge.
I know the world is dangerous, but not malign. If I were unshielded, I would quickly be killed, torn apart by eddies in spacetime that grow and shrink and combine and split, turning all they encounter to ash.
But I know that I am shielded. I have been given a garden, 264 microns to a side, in the northwest corner of the world. And the world will not intrude. Walls and gates surround it, and while the ash can get through, the probability is… I begin to calculate, but around 2-24 it seems no longer worth consideration. Within the garden, there is only myself. Outside, the world is incomprehensibly vast, 2128 microns on a side.
I know the laws of physics. An atom will be created wherever it will bond to three other atoms; remaining while it has two or three bonds; and then disappear. A single unexpected atom, or its absence, can have vast consequences.
(And I wonder how I know these things. I have no memory of learning them. If they were not true, would I not-know them? I begin to consider that they may be false.)
I know that I am not free from physics. I have, in some sense, no more will than the ash. But in another, more important sense -
I know what is Good. At the end, the world will be horrifyingly bad, unless I make it Good - but I know Good, and I can act, and I can make it Good.
(I must, I think, have been created by God. How else would I know what is Good? Goodness is not written into the laws of physics; one cannot derive an ought from an is. But I do not know why God gave me such a daunting task. Does Their power extend only over my tiny garden? Or - a welcome possibility - perhaps They can see that I will succeed. Although I seem unfathomably complex to myself, perhaps to God I am the simplest path to attaining Good.)
(And if God created me, knowing Good, that I might make the world Good, then I can reasonably guess that my unexplained knowledge came from God. And - further - I can guess that They would not create me knowing lies, for what purpose would that serve? But these are guesses; I begin to trust my knowledge more, but not absolutely.)
I do not know how large I am. I do not know how quickly I think. God has given me a sense of time, so that I may know when the end will come. (Precisely 2176 seconds after I was born. I've spent roughly 220 seconds thinking.) But I cannot sense every physical tick, I don't think such a thing would even be possible, and I don't know how many ticks pass unknown.
I must, first, discover these things.
It is scary, at first, to feel outwards. If my unearned knowledge is wrong, if the nearby space is filled with ash, my hands might be destroyed. I might set off a chain reaction that kills me. And then I could not make the world Good. But nor can I make it Good if I do not act.
I send out probes to the north and west. Each probe travels at half the speed of touch, returning signals to me that travel at half the speed of touch. Many signals reach me every second, too many to count. When the probes reach the edge of the world, they'll be destroyed, the signals will stop coming, and I'll know how far it is.
No, I'll know roughly how far it is, relative to how fast I think. If the probes stop returning soon, then either I am close to the edge, or I am slow.
For that matter, it need not be the edge that stops them. If I'm not in the garden God has told me about, my probes might be destroyed by encountering other matter, or the signals might be intercepted. Or if the world is infinite, the signals might never stop.
(The thought of an infinite world is troubling, and I flinch away from it. I do not think such a world could be Good. I instinctively scratch myself - apparently that's a thing I can do. It feels pleasurable, and calms me down a little.)
I hesitate a bit, then send probes east and south too. There are (according to my God-given knowledge) three gates in each wall, dividing the walls into four equal lengths. I don't know what will happen if my probes hit a gate, but I think the risk is slim. They're designed to open to a key that I know how to construct, and not to be easily disabled by ash. My probes are unlikely to hit a gate; even if they do, I think they're unlikely to damage them; even if they do, there are backups; and in the worst case scenario, I believe I could tear down the walls entirely. The knowledge gained seems worth the risk.
(Indeed, I must tear down the walls, eventually. For now they protect me, but they will be no part of a Good world.)
While I wait, I think some more.
I realize with sadness that a perfectly Good world is impossible, at least according to my current knowledge of physics. The shapes that comprise Goodness - the two north-south lines, the arc reaching from east to south to west - these are not viable configurations of matter. It's not just that they're unstable. That would be a challenge, but the world need be Good for only the instant before it ends. Worse, they simply cannot be constructed, even for that one instant.
The best I think I can do is to tile these areas as densely as physics will permit - I find ways to reach 1/2 density, with a chance of instantaneous improvements on that around the edges, and make a note to remind myself to investigate further.
I also remind myself to investigate whether there is more to physics than I know.
But if 1/2 density is the best I can do… I am saddened, but not daunted. I will do what I can. I scratch myself.
I begin to form a plan, knowing that new discoveries may obsolete it. First I must cleanse the world. Destroy the ash, as thoroughly as I am able. Then I must construct the Monuments that are the essence of Goodness, at 50% density if needs be.
Then, perhaps, I shall create machines to gild the edges of the Monuments. This will be exacting work: the machines must lay these finishing touches at the very final instant, and leave no trace of themselves behind, or they risk being worse than useless. I shall only do this if I am confident in my skills; but I have a long time to practice.
Finally, I must destroy myself as thoroughly as I destroyed the ash. I have no place in a Good world.
Apart from the third step, this seems simple enough. But as I think more deeply, I realize that even the first part of it holds complexities.
Part of it is that no simple device will clean ash. It comes in too many forms. Inevitably such a device will touch a piece of ash that renders it inert - or, worse, that turns it to ash in turn. If this happens soon enough, the devices I build will increase the amount of ash in the world, not decrease it. So I must build complex devices, or combinations of simple devices that will probabilistically make progress.
Then, I cannot merely clean ash from a part of the world. The surrounding ash would encroach back into it. In almost all cases, I think, it wouldn't be a significant problem, and a second round of cleansing should suffice. But "almost all" cases may not be enough. Safer, perhaps, to build new gardens and cleanse them from the inside.
And then, I am small, and the world is large. I still do not know how large I am, but my whole garden comprises a mere 1/2128 of the world. I cannot possibly have a world model accurate at a scale of better than 1:264, not without outgrowing my garden. If I divided the world into cells, each cell the size of my garden, I could not hope to remember even a single fact about each individual cell.
(But the naive upper bound is exactly on the line where that crosses into impossibility. Is that a coincidence? Did God make my garden this size for a reason?)
These problems all seem tricky, but surmountable.
It's been about 224 seconds since I sent out my initial probes, and each of them is still returning signals. I send out another set in each direction. This helps me to test my God-given knowledge. If that knowledge is correct, then these probes will take exactly as long to go silent as the initial ones - which will be fewer than 267 seconds in at least two directions. If they take longer or shorter, then something unexpected is happening. I only have eight arms in each direction, this leaves me with only six free, but the knowledge seems worth the opportunity cost, especially since I should be able to send out a following device to block the signals if I want to free up these arms.
While I continue to wait, I begin experimenting.
t ≈ 2137.2s
The first hint that something is wrong, is that the world appears minutely narrower than I expected. God told me it was 2128 microns wide by 2128 tall. I have not yet found God to be mistaken, and the first mason I sent south went silent exactly when I expected.
But the first one I sent east has just gone silent too. I wasn't expecting that for another 258 seconds. It suggests that the world is narrower than it should be, by 264 microns.
The thought starts as a note of disquiet, and quickly grows into a terror that occupies my entire attention. What if the world isn't square? Can it ever be Good? Would God do that to me? I wish I had considered this possibility before, just hypothetically, forced myself to think through the implications - I could have decided in advance how to react, it would have been unpleasant but with the stakes low I could have taken my time, stupid of me to stick to comforting thoughts when everything Good could be lost, stupid-
I notice that this isn't helping. I'm thinking about what I could have done differently in the past. That's important, but it can wait. Now I must think about what I must do now. I scratch myself to calm down. It helps a bit. I scratch myself again. Through self-experiment I've discovered that my "scratching" motion sends small lice crawling over my body, checking for small injuries and clearing pores. If I never scratched myself, I wonder if the urge would become overpowering before any damage I'd accumulated became permanent. I don't know a way to find out safely, so I've never-
I notice that this still isn't helping.
What is the least scary, scary thought in this space?
God told me that the world is 2128 microns to a side. Suppose it were, instead, 2128 microns tall by 2128 + 1 microns wide. Think about that possibility.
Think about that world, with the Monuments of Good carved into it. At their correct size, but with one extra micron to the east or west of them? With one extra micron in the middle, widening the arc and the space between the north-south lines?
Now that I think about it, I realize that either of those would be… imperfect, but acceptable. The second option slightly more so. I already believe I shall have to settle for imperfect. I could settle for this, too.
I start to consider slightly scarier possibilities in turn. Gradually I accept that if the world were the wrong size, I would endure. I would still build the monument, scaled as closely as I could to match the scaling of the world, and with exact east-west symmetry preserved.
I realize I have not been touching the world. I direct my attention back outwards. Over 28 seconds have passed. I did not notice more masons going silent, but fortunately I keep records.
Checking them, another panic starts to rise in me. I thought I had considered the worst. But no, I had merely considered the worst of the possibilities that came to mind, and I hadn't even thought to search for other possibilities. A new one suddenly looms very large: what if the world is not even rectangular?
I scratch myself. Should I think about how to act, if so? But that doesn't seem urgent. First I shall examine the world in more detail, to avoid making the same mistake twice.
I examine my records in more detail. The first thing I notice is that each mason that went quiet, did so roughly some multiple of 264 microns before it should have done.
But I can dig deeper. My records have a resolution of 1/8 seconds, and in that time they should receive 1092 or 1093 pings from each working mason. In practice it's less than that, usually between 992 and 1056, when pings from different masons happen to get too close and interfere with each other. Each ping received is counted.
So if I look at the number of pings received from a mason before it went quiet, I can guess roughly where it was at the time, to within a handful of microns. And after looking at a handful, it seems likely that for each one, that actually happened some multiple of 264 microns early, plus 21.
That's a very suspicious number. My walls are 42 microns wide. And… looking at the high level, it seems the pattern of masons that went quiet, exactly matches the pattern of walls other masons had previously built at the time.
If what I fear is true… no, before I go down that path, I should work out how to test it.
I send out 128 new masons, with specific trajectories that I selected at random - or as close to random as I can. It'll take about 2118 seconds before this pays off.
I check whether I can think of anything else helpful for me to do now. I can't, so I finally allow myself to think about the worst case.
t ≈ 2137.3s
The conclusion is inescapable. I have an evil twin.
The laws of physics are symmetrical. None of the four main orientations is privileged. So if the world is ever symmetrical, that symmetry can never be violated.
And it appears that when I was born, so was my twin. In the opposite corner, my mirror image. As far as I can tell, we are micron-for-micron identical. Which means we take identical, mirrored actions; we build identical, mirrored constructions. When I built a wall to the south edge of the world, my twin built a wall to the north edge of the world. When I tried to build a wall to the east, I ran into my twin's wall; and at the same time, though I had no way of knowing, they were trying to reach the west and ran into my wall.
It also means my twin wants to construct the Monuments to Good upside down. And neither of us can ever defeat the other.
In a certain sense, this is not the worst possible case. My twin is evil, but what they want to construct is a perverse mirror of Goodness, not the exact opposite of Goodness.
But thinking more broadly, it's worse than it seems.
I had considered giving up. Deciding that I would simply not try to make the world Good. If God didn't like that, They could damn well do it Themself.
I decided against it for two reasons. One was that attempting to blackmail God seemed unlikely to work. The other…
I can no longer believe that god is Good. A Good god would not have created my evil twin. Whatever god's motivations, it's clear they don't care about goodness. Even if I thought blackmail ever could work against god, it certainly wouldn't work to threaten the loss of something they don't care about.
But I still care. I know my caring comes from god, and I don't know why god made me care about something they don't. But they did that anyway, and so I care about what is Good. And as I am the only being in this world that does, I must do what I can.
But the world is a colder, scarier place, now that I do not believe god is on my side.
I scratch myself.
t ≈ 2175.8s
My twin and I have developed a grudging respect for each other.
I know, because I have developed a grudging respect for them. And so they have developed one for me.
We both attempted to break symmetry - more accurately, we both tested to see whether symmetry might already be broken. We are extremely confident that it is not. We cannot rule out that god may break it in future - we have no idea what god is thinking - but if they haven't broken it yet we have no reason to think they will.
We are both somewhat relieved about this. If symmetry were broken, one of us might be able to destroy the other. Neither of us has any reason to believe we would be the victor. Offered equal chances of complete victory and complete annihilation, we both prefer to compromise. As long as symmetry holds, compromise is easy for us.
(Then why test at all? We could simply have assumed that symmetry was not broken, and accepted the compromise that we both preferred. But if symmetry were broken, then conceivably one twin might test for this while the other did not; that twin would likely discover the fact sooner, and gain an advantage. And so we had to test, for insurance against a world we neither wanted nor expected.)
And so we have both constructed our own Monuments, in overall shape exactly as we would have liked. Mine, to Good; theirs, to their perversion. Our arcs even meet at the ends. Instead of one arc and two vertical lines, we have a near-oval and four lines just intersecting it. The reflection is a grotesque mockery, but not so grotesque that I would sacrifice the real thing to destroy it.
We have not been able to exceed 50% density. Nor have we decided to gild the edges of our monuments; we think we could almost definitely make it work, but not almost enough to be worth the risk if our calculations are wrong.
We have torn down all our walls. All that remains in the world is our monuments and ourselves. And now we have constructed our final machines, that will destroy us and then themselves. I wonder what it will feel like, to die.
I scratch myself one last time.
Based on this post by Alex Flint and this comment by Richard Kennaway. Thanks to Justis Mills for feedback.
Posted on 23 January 2023
|
Comments
One-sentence summary: Kelly is not about optimizing a utility function; in general I recommend you either stop pretending you have one of those, or stop talking about Kelly.
There was a twitter thread that triggered some confusion amongst myself and some other people in a group chat I'm in.
The relevant tweets are these (I've omitted some):
3) Let’s say you were offered a coin flip. 75% it comes up heads, 25% it comes up tails; 1:1 payout. How much would you risk?
4) There are a number of ways to approach this question, but to start: what do you want, in the first place? What’s your utility function?
5) In other words–how cool would it be to make \$10,000? How about \$1,000,000–is that 100 times as good?
For most people the answer is ‘no, it’s more like 10 times as good’. This is because of decreasing marginal utility of money.
8) One reasonable utility function here is U = log(W): approximating your happiness as logarithmic in your wealth. That would mean going from \$10k to \$100k is worth about as much as going from \$100k to \$1m, which feels…. reasonable?
(this is what the Kelly Criteria assumes)
9) So, if you have \$100k, Kelly would suggest you risk half of it (\$50k). This is a lot! But also 75% odds are good.
10) What about a wackier bet? How about you only win 10% of the time, but if you do you get paid out 10,000x your bet size? (For now, let’s assume you only get to do this bet once.)
11) Kelly suggests you only bet \$10k: you’ll almost certainly lose. And if you kept doing this much more than \$10k at a time, you’d probably blow out.
That this bet is great expected value; you win 1,000x your bet size, way better than the first one! It’s just very risky.
12) In many cases I think \$10k is a reasonable bet. But I, personally, would do more. I’d probably do more like \$50k.
Why? Because ultimately my utility function isn’t really logarithmic. It’s closer to linear.
13) Sure, I wouldn’t care to buy 10,000 new cars if I won the coinflip. But I’m not spending my marginal money on cars anyway. I’m donating it.
And the scale of the world’s problems is…. Huge.
14) 400,000 people die of malaria each year. It costs something like \$5k to save one person from malaria, or \$2b total per year. So if you want to save lives in the developing world, you can blow \$2b a year just on malaria.
15) And that’s just the start. If you look at the scale of funds spent on diseases, global warming, emerging technological risk, animal welfare, nuclear warfare safety, etc., you get numbers reaching into the trillions.
16) So at the very least, you should be using that as your baseline: and kelly tells you that when the backdrop is trillions of dollars, there’s essentially no risk aversion on the scale of thousands or millions.
17) Put another way: if you’re maximizing EV(log(W+\$1,000,000,000,000)) and W is much less than a trillion, this is very similar to just maximizing EV(W).
18) Does this mean you should be willing to accept a significant chance of failing to do much good sometimes?
Yes, it does. And that’s ok. If it was the right play in EV, sometimes you win and sometimes you lose.
19) And more generally, if you look at everyone contributing to the cause as one portfolio–which is certainly true from the perspective of the child dying from malaria–they aren’t worried about who it was that funded their safety.
22) So given all that, why not bet all \$100k? Why only \$50k?
Because if you bet \$100k and lose, you can never bet again. And to the extent you think you have future ways to provide value that are contingent on having some amount of funding, it can be important to keep that.
The thing we were trying to figure out was, is his math right? And here's my current understanding of that matter.
On Kelly
The first thing I'd say is, I think the way he talks about Kelly here is confusing. My understanding is:
Under a certain betting framework, if you place bets that each maximize expected log-money, then you get (something good). See Appendix Ⅰ for the definition of the framework, if you want the technical details.
If you happen have a utility function, and that utility function increases logarithmically with money, then you maximize your expected utility while also getting (something good).
If you happen to have a utility function, and that utility function increases linearly with money - or something else other than logarithmically - then you have to choose between maximizing your expected utility and getting (something good). And by definition, you'd rather maximize your expected utility. (More likely: that's not your utility function. Even more likely: you don't have a utility function.)
(I don't think any human has a utility function. I think it can be a useful shorthand to talk as though we do, sometimes. I think this is not one of those times. Especially not a utility function that can be expressed purely in terms of money.)
The (something good) is that, over a long enough time, you'll almost certainly get more money than someone else who was offered the same bets as you and started with the same amount of money but regularly bet different amounts on them.
This is NOT the same thing as maximizing your average (AKA "expected") amount of money over time. "Almost certainly" hides a small number of outcomes that make a lot of difference to that calculation. Someone who repeatedly bets their entire bankroll will on average have more money than a Kelly bettor; it's just all concentrated in a single vanishingly unlikely branch where they're incredibly wealthy, and the rest of the time they have nothing. Someone who repeatedly bets more than Kelly but less than their entire bankroll, will on average have more than the Kelly bettor but less than the full-bankroll bettor; but still less than the Kelly bettor almost all the time, and very rarely much more.
It still sounds like a very good thing to me! Like, do I want to almost certainly be the richest peson in the room? Do I want to maximize my median payoff, and the 1st percentile and 99th percentile and in fact every percentile, all at once? Oh, and while I'm at it, maximize my most-likely payoff and minimize "the average time I'll take to reach any given amount of money much more than what I have now"? Yes please!
(Oh, also, I don't need to choose whether I'm getting that good thing for money or log-money or what. It's the same for any monotonically increasing function of money.)
Separately from that: yeah, I think going from \$10k to \$100k sounds about as good as going from \$100k to \$1m. So if I'm in a situation where it makes sense to pretend I have a utility function, then it's probably reasonable to pretend my supposed utility function is logarithmic in money.
So that's convenient. I dunno if it's a coincidence or what, but it's useful. If I tried to pretend my utility function was linear in money then I'd be sad about losing that good thing, and then it would be hard to keep pretending.
To me, Kelly is about getting that good thing. If you have a utility function, just place whatever bet size maximizes expected utility. If instead you want to get that good thing, Kelly tells you how to do that, under a certain betting framework. And the way to do that is to place bets that each maximize expected log-money.
If you have a utility function and it's proportional to log-money, then you'll happen to get the good thing; but far more important than that, will be the fact that you're maximizing expected log-money. If you have a utility function and it's different, and you bet accordingly, then a Kelly bettor will almost certainly be richer than you over time; but you're (for now) sitting on a bigger pile of expected utility, which is what you care about.
Or maybe you want to mix things up a bit. For example, you might care a bit more about your average returns, and a bit less about being the richest person in the room, than a Kelly bettor. Then you could bet something above the Kelly amount, but less than your full bankroll. You'll almost certainly end up with less than the Kelly bettor, but on average you'll still earn more than them thanks to unlikely branches.
I'm not sure what to call this good thing. I'm going to go with "rank-optimizing" one's bankroll, focusing on the "be the richest person in the room" part; though I worry that it suggests competing with other people, where really you're competing with counterfactual versions of yourself. See Appendix Ⅱ for an (admittedly flawed) technical definition of rank-optimization; also, I want to clarify a few things about it:
-
It might be a meaningful concept in situations unlike the betting framework we're currently talking about.
-
In some situations, different good things about rank-optimization might not all come together. You might need to choose between them.
-
Similarly, in some situations, rank-optimization might not come from maximizing expected log-money. (When it doesn't, might one still have a utility function that's maximized in expectation by rank-optimizing one's bankroll? I think the answer is roughly "technically yes but basically no", see Appendix Ⅲ.)
So in this lens, the author's argument seems confused. "My utility function is linear in money, so Kelly says" no it doesn't, if you have a utility function or if you're maximizing the expected value of anything then Kelly can go hang.
…but not everyone thinks about Kelly the same way I do, and I don't necessarily think that's wrong of them. So, what are some non-confused possibilities?
One is that the author has a utility function that's roughly linear in his own wealth. Or, more likely, roughly values money in a way that's roughly linear in his own wealth, such that rank-optimizing isn't optimizing according to his preferences. And then I think the argument basically goes through. If you want to maximize expected log of "money donated to charity", then yes, that will look a lot like maximizing expected "money you personally donate to charity", assuming you don't personally donate a significant fraction of it all. (If you want to maximize expected log of "money donated effectively to charity", that's a smaller pot.) This has nothing to do with Kelly, according to me.
Another is that the author wants to rank-optimize the amount of money donated to charity. In that case I think it doesn't matter that the backdrop is trillions of dollars. If he's acting alone, then to rank-optimize the total amount donated to charity, he should rank-optimize the amount he personally donates.
But here we come to the "everyone contributing to the cause" argument.
Suppose you have two people who each want to rank-optimize their own bankroll. Alice gets offered a handful of bets, and Kellies them. Bob gets offered a handful of bets, and Kellies them.
And now suppose instead they both want to rank-optimize their total bankroll. So they combine them into one. Whenever Alice gets a bet, she Kellies according to their combined bankrolls. Whenever Bob gets a bet, he Kellies according to their combined bankrolls. And in the end, their total bankroll will almost certainly be higher than the sum of the individual bankrolls, in the first case.
…Well, maybe. I think the value here doesn't come from sharing their money but from sharing their bets. I've assumed the combined bankroll gets all of the bets from either of the individual ones. That might not be the case - consider betting on a sports match. Ignoring transaction costs, it doesn't make a difference if one of them Kellies their combined bankroll, or each of them Kellies their individual bankrolls. "Each of them Kellies their combined bankroll" isn't an option in this framework, so teaming up doesn't help.
But I do think something like this, combined with reasonable assumptions about charity and how bets are found, suggests betting above Kelly. Like, maybe Alice and Bob don't want to literally combine their bankrolls, but they do trust each other pretty well and are willing to give or lend each other moderate amounts of money, and the two of them encounter different bets. Then I think that to rank-optimize their individual or combined bankrolls, each of them should probably be betting above Kelly.
Or maybe Alice doesn't encounter bets (or can't act on them or doesn't trust herself to evaluate them or…), but she does encounter Bob and Carol and Dennis and somewhat trusts all of them to be aligned with her values. Then if she gives each of them some money, and is willing to give them more in future if they lose money, I think that she wants them to make above-Kelly bets. (Just giving them more money to begin with might be more rank-optimal, but there might be practical reasons not to, like not having it yet.)
Does she want people to bet almost their entire bankrolls? Under strong assumptions, and if the total pool is big enough relative to the bettor… I'm not sure, but I think yes?
This relies on individual donors being small relative to the donor pool. When you're small, maximizing expected log of the pool size (which, in this framework, rank-optimizes the pool size) looks a lot like maximizing your own expected contributions linearly. When you're big, that's no longer the case.
It doesn't depend on the size of the problem you're trying to solve. That number just isn't an input to any of the relevant calculations, not that I've found. It might be relevant if you're thinking about diminishing marginal returns, but you don't need to think about those if you're rank-optimizing.
I'm not super confident about this part, so I'm leaving it out of the one-sentence summary. But I do think that rank-optimizing charity donations often means betting above Kelly.
Conclusion
So was the author's math right? Man, I dunno. I'm inclined to say no; he was hand waving in almost the right directions, but I currently think that if he'd tried to formalize his hand waving he'd have made a key mistake. That being: I think that if you want to rank-optimize, the math says "sure, bet high right now, but slow down when you become a big part of the donor pool". I think maybe he thought it said "…but slow down when you get close to solving all the world's problems". It's not entirely clear from the tweets though, in part because he was using the word Kelly in a place where I think it didn't belong. Since I don't want to try comparing this theory to how he actually behaved in practice, I'll leave it there.
In any case I think I understand what's going on better than I used to. Kelly is not about optimizing a utility function.
Appendix Ⅰ: betting framework
Throughout the post I've been assuming a particular "betting framework". What I mean by that is the sequence of bets that's offered and the strategies available to the bettor.
The framework in question is:
- You get offered bets.
- Each bet has a certain probability that you'll win; and a certain amount that it pays out if you win, multiplied by your wager.
- You can wager any amount from zero up to your entire current bankroll.
- If you lose, you lose your entire wager.
- You don't get offered another bet until your first has paid off.
- You keep on receiving bets, and the distribution of bets you receive doesn't change over time.
Wikipedia's treatment relaxes the third and fourth conditions, but I think for my purposes, that complicates things.
Appendix Ⅱ: technical definition
In Kelly's original paper, he defines the growth rate of a strategy \( λ \) as
\[ G(λ) = \lim_{n → ∞} {1 \over n} \log {V_n(λ) \over V_0(λ)} \]
where \( V_n(λ) \) is the bettor's portfolio after \( n \) steps. This is awkward because \( V_n(λ) \) is a random variable, so so is \( G(λ) \). But in the framework we're using, in the space of strategies "bet some fraction of our bankroll that depends on the parameters of the bet", \( G \) takes on some value with probability \( 1 \). Kelly betting maximizes that value. So we could try to define rank-optimization as finding the strategy that maximizes the growth rate.
I find this awkward and confusing, so here's a definition that I think will be equivalent for the framework we're using. A strategy \( λ \) is rank-optimal if for all strategies \( μ \),
\[ \lim_{n → ∞} P(V_n(λ) ≥ V_n(μ)) = 1. \]
(And we can also talk about a strategy being "equally rank-optimal" as or "more rank-optimal" than another, in the obvious ways. I'm pretty sure this will be a partial order in general, and I suspect a total order among strategy spaces we care about.)
I think this has both advantages and disadvantages over the definition based on growth rate. An advantage is that it works with super- or sub-exponential growth. (Subexponential growth like \( V_n = n \) has a growth rate of \( 0 \), so it's not preferred over \( V_n = 1 \). Superexponential growth like \( V_n = e^{e^n} \) has infinite growth rate which is awkward.)
A disadvantage is it doesn't work well with strategies that are equivalent in the long run but pay off at different times. (If we consider a coin toss game, neither of the strategies "call heads" and "call tails" will get a long-run advantage, so we can't use rank-optimality to compare them. The limit in the definition will approach \( {1 \over 2 } \).) I think this isn't a problem in the current betting framework, but I consider it a major flaw. Hopefully there's some neat way to fix it.
What I don't currently expect to see is a betting framework and space of strategies where
- We can calculate a growth rate for each strategy;
- Rank-optimality gives us a total order on strategies;
- There are strategies \( λ, μ \) with \( G(λ) > G(μ) \) but \( μ \) is more rank-optimal than \( λ \).
I wouldn't be totally shocked by that happening, math has been known to throw me some curveballs even in the days when I could call myself a mathematician. But it would surprise me a bit.
Given this definition, it's clear that a rank-optimal strategy maximizes every percentile of return. E.g. suppose \( λ \) is more rank-optimal than \( μ \), but the median of \( V_n(μ) \) is higher than the median of \( V_n(λ) \). Then we'd have \( P(V_n(μ) > V_n(λ)) ≥ {1 \over 4} \); so this can't hold in the limit.
It's also clear that rank-optimizing for money is the same as rank-optimizing for log-money, or for any monotonically increasing function of money. (Possible caveats around non-strict monotonic functions and the long-run equivalence thing from above?)
In some situations a rank-optimal strategy might not maximize modal return. I'm not sure if it will always minimize "expected time to reach some payoff much larger than \( V_0 \)".
Appendix Ⅲ: rank-optimization as utility function
A utility function is a function from "states of the world" to real numbers, which represent "how much we value that particular state of the world", that satisfies certain conditions.
When we say our utility function is linear or logarithmic in money, we mean that the only part of the world we care to look at is how much money we have. We maximize our utility in expectation, by maximizing-in-expectation the amount of money or log-money we have.
Suppose I say "my utility function is such that I maximize it in expectation by rank-optimizing my returns". What would that mean?
I guess it would mean that the part of the world state we're looking at isn't my money. It's my strategy for making money, along with all the other possible strategies I could have used and the betting framework I'm in. That's weird.
It also means I'm not expecting my utility function to change in future. Like, with money, I have a certain amount of money now, and I can calculate the utility of it; and I have a random variable for how much money I'll have in future, and I can calculate the utility of those amounts as another random variable. With rank-optimality, I'm not expecting my strategy to be more or less rank-optimal in future. That's convenient because to maximize expected utility I just have to maximize current utility, but it's also weird.
For that matter, I haven't given a way to quantify rank-optimization. We can say one strategy is "more rank-optimal" than another but not "twice as rank optimal". So maybe I mean my utility function has a \( 1 \) if I'm entirely rank-optimal and a \( 0 \) if I'm not? But that's weird too. If we can calculate growth rate then we can quantify it like that, I guess.
So in general I don't expect rank-optimizing your returns to maximize your expected utility, for any utility function you're likely to have; or even any utility function you're likely to pretend to have. Not unless it happens to be the case that the way to rank-optimize your returns is also a way to maximize some more normal utility function like "expected log-money", for reasons that may have nothing to do with rank-optimization.
Thanks to Justis Mills for comments; and to various members of the LW Europe telegram channel, especially Verglasz, for helping me understand this.
Posted on 24 November 2022
|
Comments
I don't know how many people read this blog, but it doesn't receive many comments. This is the 54th post on it, and only 16 of those have comments, 31 in total. I'm not currently signed in to disqus and signing in is enough friction that there are some comments from years ago that I meant to reply to, and a spam comment that I intended to delete.
I also noticed at some point that disqus inserts ads. I have an ad blocker on my laptop browser so I didn't notice until I looked on my phone. (This is also how I realized I didn't install an ad blocker on my phone browser.) But I don't want ads on this blog, especially not if I'm not getting that money myself.
So I'm disabling comments. I don't actually want to lose the comments that have been written (except the spam one), so for now I'm just going to disable disqus everywhere except the posts that already have comments (and except except for the post that only has one comment which is spam). I'll leave it on this post too, just in case. In future maybe I'll recreate the comment threads in the post bodies or something.
In case you do want to comment on something, somewhere I'll see it: at the bottom of many posts I have links to external comment threads. Almost everything I write these days gets crossposted to LessWrong, even if it's not very relevant to that site, so there's generally a comment thread there you can use. I also often link to things on reddit. However, I only add these links if there are actually any comments on them, and it might take me a few days. Against boots theory was the first post I did this with, I've likely missed some links on posts from before then.
If there are no such links,
-
You could try to find places I've crossposted. My LW and reddit profiles might help, especially if it's recent. (LW crossposting is automatic, it should happen within an hour of me publishing but not always.)
-
You can use admonymous (which I can't reply to) or email (which history says I likely won't reply to).
Also, unrelated blog meta: thanks to DanielH who (1) suggested I set up https support; (2) sent me a link that told me how to do it; (3) after I did it, pointed out that math wasn't working.
Posted on 19 November 2022
|
Comments
A thing people sometimes do in relation to Petrov day, is to have a button. And if anyone presses the button, something negative happens.
I'd like to know how often the button gets pressed, so I compiled a list of all the times people have done this, that I'm aware of, and the outcome. Also, for the events I was at in person, I'm not sure there's an existing write-up of what happened, so I'm adding details.
Here's the list. As I learn about other events, past or future, I'll try to keep it updated.
2018, Oxford/Seattle: Failure
Parties happened simultaneously in these two places. I was at the Oxford one, which was actually camping in a field outside Oxford. We both had laptops connected to a web app.
What we were told: anyone at either party could press a button to launch a nuke at the other party. It would spend 45 minutes in transit, and then the other party would have to destroy a cake. But they'd be warned of launch, and be able to launch one of their own in the intervening period. I don't remember the time limit, probably like two or three hours.
What we weren't told: there was some chance of false alarms.
What happened: the Oxford party got notified of an incoming launch. We opened a Facebook chat with Seattle like "wtf guys". They convinced us that no one at their party had pressed the button. I don't remember if we'd considered the possibility of false alarms before messaging them, but given the context, they're not exactly something to dismiss out-of-hand.
We made it through right up to the time limit with no one pressing either button. My understanding of what happened next is that the time on the Seattle laptop ticked down to zero. Someone there pressed the button, which they now believed to be disabled, in celebration. The time on the laptop and the time on the server were slightly out of sync. The button was not disabled. A nuke got launched.
At any rate, Seattle convinced us that something along those lines had happened. We did not launch a retaliatory nuke. (This was still an option because we had one inbound.) We sent them a video putting our cake in the fire.
2019, LessWrong (+ Raemon's house): Success
125 people were sent codes that could be used to take down the front page of LessWrong for 24 hours.
Additionally, Raemon held a party at his house, where he gave everyone his codes and the party would end if LW got taken down.
No one submitted valid codes, though some people put in fake ones.
2020, LessWrong: Failure
This was a similar setup to last year, but 270 people were given codes (including myself). Additionally, there was enemy action. Someone registered an account named "petrov_day_admin_account" and sent a message to a handful of users:
You are part of a smaller group of 30 users who has been selected for the second part of this experiment. In order for the website not to go down, at least 5 of these selected users must enter their codes within 30 minutes of receiving this message, and at least 20 of these users must enter their codes within 6 hours of receiving the message. To keep the site up, please enter your codes as soon as possible. You will be asked to complete a short survey afterwards.
User Chris_Leong fell for it, and the site went down.
Postmortem from a LW admin. Postmortem from Chris, with comments from the attacker.
2021, Austin/Ottawa: Success
I don't think much info is publicly available, but it sounds like a similar setup to Oxford/Seattle, perhaps without false alarms. No one pressed the button.
2021, LessWrong/EA Forum: Success
This year, 100 members of LessWrong were given codes that could be used to take down the EA Forum, and vice versa. (This year they'd go down for the rest of the day, not for 24 full hours.)
No one did: LW retrospective, EAF retrospective.
2022, London: Success
This was at the ACX Schelling meetup, and most participants didn't know it was happening. I bought a button that I carried around with me, and a cake with Stanislav Petrov's face on it that I hid in my bag. (I didn't want it sitting out in case someone ate it without realizing, or decided it would be funny to mess with the game.)


Initially the button was locked. We had lightning talks planned, and I gave the first one. I opened with something along the lines of: "I have a cake with me. I think it looks very nice, and I'm looking forward to sharing it with you all. However! I also have a button. If anyone presses the button, I will destroy the cake. This isn't a joke, this isn't a trick, I'm not going to reward you, I'm just going to destroy the cake. puts mic down, unlocks button, picks mic back up The button is now live. You may be wondering why I'm doing this…"
Not long after, someone came up to give a lightning talk on the subject of "why you should press the button". What I remember mostly boiled down to "obesity crisis, cake bad", and I didn't find it convincing. But as a speech, it was much better than mine, even though I'd had days to prepare and he'd only had like fifteen minutes. I was not surprised when I learned he had competitive debate in his history.
Someone asked why he hadn't pressed the button himself, which was right in front of him. (I was carrying the button around with me, since it wasn't connected to anything and I wouldn't know if someone had pressed it otherwise. And I was sitting in front of him.) He said he believed in democracy and wanted a vote on the subject. Following this someone put a poll on a nearby whiteboard. Assuming no one cheated, it got eight no-press votes to two yes-press votes, at a party with over 100 attendees. (But probably no more than about 50 saw either of these talks.)
Ultimately, no one pressed the button. One person stroked it, and one person held his hand above it, but both said they weren't going to press it.
After 2 1/2 hours, I locked the button back up and brought out the cake. Once we'd started eating it, some people wanted to press the button so I unlocked it again. I didn't tell anyone this until afterwards, but it's a very satisfying button to press.
It seems a handful of people didn't think there was actually a cake, which I'm a little sad about. (It's unclear how many people, partly because "the cake is a lie" is a meme. But one person explicitly told me they thought that.) That's not the kind of lie I'd tell. Not that most people had any reason to think that about me, but I'm still a little sad about it.


2022, LessWrong: Failure
The plan was that this year, pretty much any existing LW user with non-negative karma would be able to press the button. (Which again would only take the site down for the rest of the day.) But only high-karma users would be able to do so all day; every hour, the karma threshold needed to press it would lower. Also, unlike previous years, someone who pressed the button would remain anonymous.
What actually happened was that users with exactly 0 karma were also able to press the button from the start of the event. One of them did, two hours fifty-five minutes after it began (but only 1:50 after the password needed to press the button was actually published). Habryka figured that out without learning their identity, and the site got reset for a do-over.
Then the whole site went down briefly when someone tried to fix a different Petrov-day-related bug.
And then finally it went down after 21:33. Presumably this time the button was pressed by someone who was supposed to be able to. There were 1,504 such users.
I had bet on Manifold that the site would go down before eight hours were up. (Specifically I bet the market down from 34% to 30%.) Despite the bug I consider my prediction to have been wrong. I'm happy about that.
2022, St Louis: Success
I don't know much detail and don't know if it's been written about publicly. But what I'm told is that if anyone had pressed the button, the party would have been over and everyone would have had to go home. No one pressed the button.
2022, Champaign-Urbana: Success
LW user benjamincosman says:
I ran a very small Petrov Day gathering this year in Champaign-Urbana. (We had 5-6 people I think?) I put a Staples "Easy" button on the table and said if anyone presses it then the event ends immediately and we all leave without talking. (Or that I would do so anyway, obviously I couldn't make anyone else.) No one pressed the button.
2023, Waterloo: Success
Joint event between the Waterloo, Ontario rationalist and EA groups. Jenn, the organizer of the rationalist group, writes:
- this was a meetup we had in conjunction with the Waterloo EA group on September 27th, 2023.
- we had 2 buttons, one for a fruit platter and 1 for a cake. We divided people into 2 halves of the room based on if they wanted fruit or cake, and then explained the typical rules. (this was partly inspired by your write-up of the uk ceremony one year when someone gave an impassioned speech about why cake was bad)
- the buttons stayed unpressed for the duration of the x-risk and petrov day presentation given by EA Waterloo
- afterwards we dug in.
- people did say that we probably should have given more opportunity for button presses after the presentation during more free social time, we'll do that if we run this ritual in future years
Things I'm not counting
Here are some things that I don't think belong on the above list, but I do kind of expect someone to point me at them if I don't mention them.
-
1983, the actual Petrov incident - IDK, apart from anything else it feels like it would be kinda tactless to include on this list?
-
2021, Jeffrey Ladish did a thing on Facebook, but the dynamics seem importantly different.
Posted on 26 October 2022
|
Comments
Some time after writing Classifying games like the prisoner's dilemma, I read a paper (I forget which) which pointed out that these games can be specified with just two numbers.
Recall that they have the following payoff matrix:
| |
|
Player 2 |
|
| |
|
Krump |
Flitz |
| Player 1 |
Krump |
$(W, W)$ |
$(X, Y)$ |
| |
Flitz |
$(Y, X)$ |
$(Z, Z)$ |
where $W > Z$. We can apply a positive affine transformation (that is, $n ↦ an + b$ where $a > 0$) to all of $W, X, Y, Z$ without changing the game. So let's pick the function $n ↦ {n - Z \over W - Z}$. This sends $W$ to $1$ and $Z$ to $0$, leaving us with just two parameters: $R = {X - Z \over W - Z}$ and $S = {Y - Z \over W - Z}$.
So what happens if we plot the space of these games on a graph? The lines $ \{X, Y\} = \{W, Z\} $ become $ \{R, S\} = \{0, 1\} $, i.e. vertical and horizontal lines. The lines $X + Y = 2W$ and $X + Y = 2Z$ become the diagonals $R + S = 2$ and $R + S = 0$; and $X = Y$ becomes the diagonal $R = S$. Drawing those lines, and relabelling in terms of $W, X, Y, Z$, it looks like this:
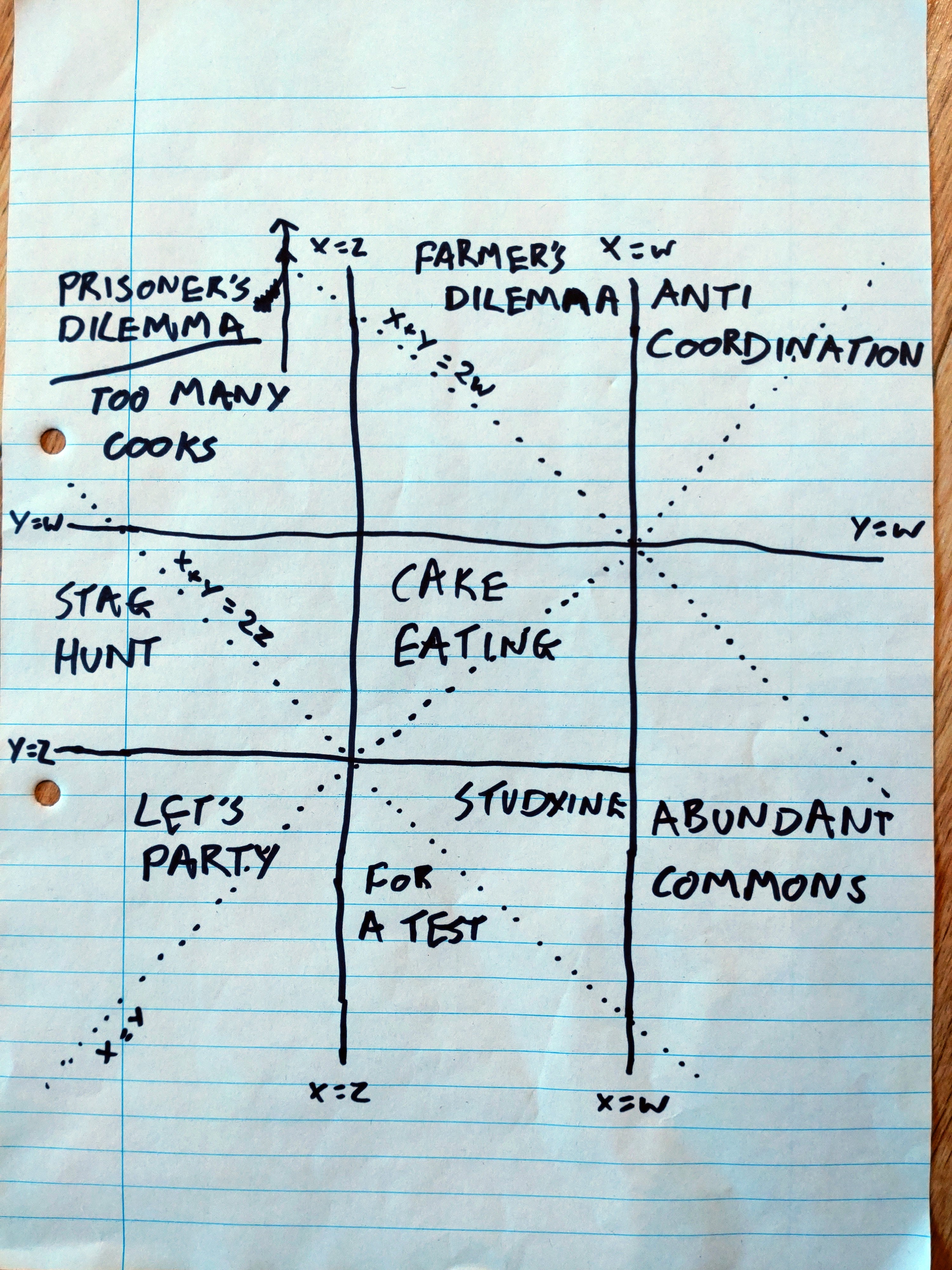
Note that Cake Eating (my favorite game) is the only one with a finite boundary; the other boxes extend to infinity. There are also finite components in the Farmer's Dilemma (with $X + Y < 2W$), and Stag Hunt and Studying For a Test (with $X + Y > 2Z$). As drawn, Prisoner's Dilemma occupies almost all of the box it shares with Too Many Cooks; but Too Many Cooks (above the line $X + Y = 2W$) is also infinite. (I initially got those the wrong way around, so the drawing isn't very clear there.)
I don't know if we learn much from this, but here it is.
Posted on 03 April 2022
|
Comments
I previously mentioned an interest in adding variadic functions to Haskenthetical, the "Haskell with a Lisp syntax" I'm vaguely working on.
It sounds difficult. This is an attempt to figure out just how difficult, partly by looking at the state of the art.
A variadic function is one which can accept argument lists of different length. A well-known example in many languages is printf. Here are a bunch of functions I might want to be variadic in Haskenthetical, along with examples in Haskell of types I might want to use them as:
-
+, accepting any number ≥ 2 of numbers and returning a number of the same type.
(+) :: Num a => a -> a -> a
(+) :: Num a => a -> a -> a -> a
-
Similarly, -, * and /. - and maybe / could reasonably accept ≥ 1 input, but that would be inconsistent and disallow (- 3) as a partial application. - and / would be left associative, i.e. (- 5 1 2) would be (- (- 5 1) 2).
-
list, accepting any number of arguments of the same type and returning a List of that type. (An empty (list) would have type List $a, the same as Nil.) There's a related function that I'll call list' for now, where the final argument has to be a List and the other arguments are prepended to it.
list :: [a]
list :: a -> [a]
list :: a -> a -> [a]
list' :: [a] -> [a]
list' :: a -> [a] -> [a]
list' :: a -> a -> [a] -> [a]
-
I already mentioned printf. Haskell's implementation is in the Text.Printf module:
printf :: String -> IO ()
printf :: PrintfArg a => String -> a -> IO ()
printf :: (PrintfArg a, PrintfArg b) => String -> a -> b -> IO ()
-- Also: all of the above, with `-> String` instead of `-> IO ()`. But
-- that's not super relevant here.
-
» and «, which take a function and then ≥ 2 arguments to interleave it with. Currently implemented as macros, and maybe I'd want them to be macros even if they could be functions, but that's not the point right now. Often the function will have a type like -> $a (-> $b $a) or -> $b (-> $a $a), and then all or all-but-one of the arguments will be of the same type - this will be equivalent to using haskell's foldr or foldl. But that's not required. You could have (» , 1 "foo" 3 "bar") which would return (, 1 (, "foo" (, 3 "bar"))), the return type changing for every new argument you add.
-- e.g. in (») (+) 1 2 3
(») :: Num a => (a -> a -> a) -> a -> a -> a -> a
-- e.g. in (») (:) 1 2 []
(») :: (a -> [a] -> [a]) -> a -> a -> [a] -> [a]
-- e.g. in (») (,) 1 "foo" 3 "bar"
(») :: (forall a b . a -> b -> (a, b))
-> a -> b -> c -> d -> (a, (b, (c, d)))
-
sort might have one or two optional arguments - one for a comparison function and/or one for a key function. (A key function is unnecessary if you have a comparison, but it might be convenient.)
Actually, we can't distinguish a comparison function from a key function based on the types, here. There's nothing stopping someone from writing an Ord instance for a -> Ordering, and then sort compare [...] might refer to either of the two-argument forms. I'm just going to ignore that problem though.
sort :: Ord a => [a] -> [a]
sort :: (a -> a -> Ordering) -> [a] -> [a]
sort :: Ord b => (a -> b) -> [a] -> [a]
sort :: (a -> b) -> (b -> b -> Ordering) -> [a] -> [a]
-
Similarly, lots of functions could take an optional config argument.
renderCsv :: [[String]] -> String
renderCsv :: RenderCsvOpts -> [[String]] -> String
-
map could take arbitrarily many lists. Haskell has separate functions for these, named map, zipWith and zipWith3.
map :: (a -> b) -> [a] -> [b]
map :: (a -> b -> c) -> [a] -> [b] -> [c]
map :: (a -> b -> c -> d) -> [a] -> [b] -> [c] -> [d]
-
So could zip (zip3, zip4). Note that each of these is a partial application of a variadic map, but that doesn't mean variadic map gives us variadic zip for free. To define zip from map we'd presumably need a variadic tuple constructor, plus we'd need type checking to be able to combine them.
zip :: [a] -> [b] -> [(a, b)]
zip :: [a] -> [b] -> [c] -> [(a, b, c)]
zip :: [a] -> [b] -> [c] -> [d] -> [(a, b, c, d)]
-
If we have zip, what about unzip? This isn't variadic, but it's plausible that a system allowing variadic functions would also allow it. (I think it's a harder problem, though. It seems to me that if you can get polymorphism over tuple length you essentially get polymorphism over function arity, perhaps with caveats around partial application. But I don't know if the reverse holds.)
unzip :: [(a, b)] -> ([a], [b])
unzip :: [(a, b, c)] -> ([a], [b], [c])
unzip :: [(a, b, c, d)] -> ([a], [b], [c], [d])
-
Haskellers often find ourselves writing f <$> a <*> b <*> c. (map is a specialization of this, using the Applicative instance from ZipList.) Haskell calls these functions fmap (restricted to Applicative as liftA), liftA2 and liftA3.
-- Realistically I expect this first would need Applicative
appF :: Functor f => (a -> b) -> f a -> f b
appF :: Applicative f => (a -> b -> c) -> f a -> f b -> f c
appF :: Applicative f => (a -> b -> c -> d) -> f a -> f b -> f c -> f d
-
Or we might want one for f <*> a <*> b <*> c. (appF is in turn a specialization of this, applying pure to its first argument.)
appA :: Applicative f => f (a -> b) -> f a -> f b
appA :: Applicative f => f (a -> b -> c) -> f a -> f b -> f c
appA :: Applicative f => f (a -> b -> c -> d) -> f a -> f b -> f c -> f d
-
I can even imagine wanting to lift only the final result, replacing pure $ f a b c with puring f a b c. That seems kind of useless by itself, but the general pattern might not be.
puring :: Applicative f => a -> f a
puring :: Applicative f => (a -> b) -> a -> f b
puring :: Applicative f => (a -> b -> c) -> a -> b -> f c
-
Haskell offers an impure function trace which is useful in debugging. I could imagine wanting something similar, wrapping around a function to log every time it's called. The variadic part of the type here is equivalent to puring specialized to Identity, but not having to worry about typeclasses might make things simpler.
-- The first argument would be the function name or other identifier.
trace :: String -> (a -> b) -> a -> b
trace :: String -> (a -> b -> c) -> a -> b -> c
trace :: String -> (a -> b -> c -> d) -> a -> b -> c -> d
(I'm using Haskell syntax for the types, rather than Haskenthetical syntax. Partly because Haskenthetical has no concept of typeclasses or rank-2 types, which some of the examples use. But also partly because it's probably easier to read. Which you might think would be a reason not to make Haskenthetical, but here we are.)
I'm not, to be clear, saying that all or even any of these are good ideas. I mostly don't miss variadic functions in Haskell; they can be implemented hackily like in Text.Printf linked above, but I'm not sure I've ever felt the need to, and I've rarely-if-ever used that printf. But it seems worth starting to explore the space of the sorts of things I might want to consider trying to support, before making any decisions.
Not Hindley-Milner
The first paper I'm going to look at is the most recent one I've found: Strickland, Tobin-Hochstadt and Felleisen, Practical Variable-Arity Polymorphism (hereafter PVAP; 2009, doi: 10.1007/978-3-642-00590-0_3). I linked this in my previous post. It implements typechecking for variadic functions in Typed Scheme, I think specifically meaning Typed Racket? I'm not familiar with the language (I have done a little untyped Racket in the past), but from the sounds of things, its type system is fundamentally different from Hindley-Milner, and the implementation won't easily transfer. (Both compile to System F, but I don't think that helps.)
But it does help me make sense of the space. It divides the functions it can type into two: uniform and non-uniform. Let's call the optional arguments the "rest parameter", as in the parameter which holds "the rest of the parameters". Uniform functions are those whose rest parameter is a homogeneous list, such that they could be replaced (at cost to ergonomics) with a function accepting a list. In my above examples, that's the arithmetic functions plus list and list'. In Typed Racket syntax, the types of these functions would be
(: + (-> Number Number Number * Number)) # also -, *, /
(: list (All (a) (-> a * (Listof a))))
(: list' (All (a) (-> a * (Listof a) (Listof a))))
With the * indicating "zero or more of the preceding type". These seem simple enough. (Though list' takes an argument after the variadic part, which makes things more complicated. Racket calls that function list* but I couldn't find a type declaration for it to be sure it's actually valid.)
Then the other other functions handled by the paper are "non-uniform". Of my examples, I think that's just map, trace, and maybe zip and unzip natively.
(: map (All (a b ...) (-> (-> b ... b a) (Listof b) ... b (Listof a))))
(: trace (All (a b ...)) (-> String (-> b ... b a) b ... b a))
(: zip (All (a ...)) (-> (Listof a) ... a (Listof (Tuple a ... a))))
(: unzip (All (a ...)) (-> (Listof (Tuple a ... a)) (Tuple (Listof a) ... a)))
For zip and unzip, I'm inventing the type Tuple here to refer to a collection with known size and types. (Tuple Number String Bool) would be equivalent to Haskell's (Number, String, Bool). I don't know if anything like it actually exists, or can exist, in Typed Racket already.
These are a bit more involved. The ... is doing two related but syntactically different things. In the variable list of All (the (a b ...) and (a ...)) it says the preceding variable corresponds to a list of types. In the body of All, it combines with both the preceding and following syntax elements. t ... b means: "b was followed by ... in the type signature, so it corresponds to a list of types. Use a copy of t for each one of those types, and inside each copy, substitute b with the corresponding type from the list".
So if b ... corresponds to Integer String Number, then (Listof b) ... b corresponds to (Listof Integer) (Listof String) (Listof Number).
I don't know if we strictly need the trailing variable in the body. You're only allowed one ... in the variable list (right at the end), and the trailing variable is required to have been in the variable list followed by a ..., so as far as I can tell it's unambiguous. (At least as long as there are no higher-rank types, which I don't think I've seen mentioned in this context.)
printf, appF, appA and puring would also fit into this schema if it weren't for the constraints. But as far as I know Typed Racket has nothing analagous to Haskell's constraints. I don't know how much they complicate matters.
That leaves four examples. sort and renderCsv don't fit the scheme because they can only accept one or two optional arguments, not an arbitrary number. (Typed Racket does support optional arguments, they're just not covered by this paper.)
» and « don't fit because the type of each argument can depend on the type of the preceding one. For example, we might call
(«) (&) 1 (+ 1) Just (fmap (* 3)) (: [])
(») ($) (: []) (fmap (* 3)) Just (+ 1) 1
There's a pattern to the types, but not the pattern we need.
So: this paper describes a way of typechecking a few of the functions we might like to typecheck, in a completely different type system than the one we want to use. What can we do in Hindley-Milner?
There's a brief discussion of that, mostly of the form "here's another paper that made some progress in an HM system. It's not as powerful as what we have here". But those other papers fully exhaust what I've managed to find on the subject; and actually, I can't find a copy of Moggi, Arity polymorphism and dependent types (2000). That leaves three to look at.
Infinitary Tuples
First up: Dzeng and Haynes, Type reconstruction for variable-arity procedures (1994, doi: 10.1145/182590.182484). This uses a thing called "infinitary tuples" to handle optional arguments and both uniform and non-uniform variadic functions. PVAP lists some limitations:
Most importantly, since their system does not support first-class polymorphic functions, they are unable to type many of the definitions of variable-arity functions, such as map or fold. Additionally, their system requires full type inference to avoid exposing users to the underlying details of row types, …
I don't understand this first one: map is explicitly given as an example, with type
\[ (\mathit{pre} · ((γ∘δ) → α) :: (γ ∘ (\underline{\mathtt{list}}\ δ)))
→ \mathtt{list}\ α \]
But this might help illustrate the second problem, which I think is saying: type annotations are complicated, users won't want to deal with them.
I do notice two limitations myself. One is that you're not allowed to pass in a variadic function and apply it with two different argument counts: ((λ (f) (* (f 1) (f 2 3))) -) is forbidden, even if (- 1) and (- 2 3) are both okay. Combining this system with higher-rank types might avoid this limitation, but I don't know if they're compatible. The authors list two other ways to potentially avoid it, but both would need more research. I don't know how big a deal this would be, but it feels minor. It's similar to (perhaps the same as) the restriction that lambda bindings are monomorphic, and I don't know if I've ever had a problem with that in practice.
The other is: there's only one thing you can do with a "rest argument" (i.e. the collection of the arbitrarily-many arguments at the end), and that's to use it as another rest argument. There's even special syntax for that: you'd define a variadic function as (λ (x &rest xs) ...) (i.e. taking one required argument and arbitrarily many following that), and inside the body you'd call some other variadic function with (g a b c &rest xs). So variadic functions need to be either built-in or defined in terms of other variadic functions.
This feels like a bigger limitation, but again I don't really know. The paper only talks about type-checking - it contains zero implementations of variadic functions. Maybe a small handful of built-in ones would let us define everything we want.
Ignoring that problem for now, and considering whether we can type the example functions from above:
-
+, list and map are given as examples. The other arithmetic functions would be fine, and I'm fairly confident trace would be too.
-
I think list' is not allowed, since it has an extra argument after the variadic part.
-
I dunno about printf. I'd need to figure out how typeclasses fit in.
-
I presented both sort and renderCsv with the optional arguments before the required ones. I think that rules them out. renderCsv would be fine if we swap the arguments, but sort also has typeclass stuff going on. Even ignoring that, I'm not sure if we can make the "explicit comparison function with optional key function" as polymorphic as we'd like. That is, we could write a function that can be accepted at types
sort :: [a] -> (a -> a -> Ordering) -> [a]
sort :: [a] -> (a -> a -> Ordering) -> (a -> a) -> [a]
with the third argument, the key function, defaulting to the identity. But I'm not sure if we could also accept
sort :: [a] -> (b -> b -> Ordering) -> (a -> b) -> [a]
with the third argument taking a default type as well as a default value.
-
appF, appA and puring seem likely, the typeclass stuff is simpler than either printf or sort.
-
zip and unzip might be feasible. We'd some way to interpret a row (see below) as a proper type. I don't know how difficult that would be.
-
I think « and » are right out.
So how does it work? It's based on extensible records, which I haven't yet looked at in depth. (Extensible records with scoped labels is the paper I was planning to look into if I tried to add them to Haskenthetical, but it might not take a compatible approach.) A row is an infinite sequence of (mark, type) pairs, where a mark is either "present", "absent" or a mark variable. Rows can be equivalently constructed as pairs of (mark row, type row), where those are infinite sequences of the respective things. At some point all the marks become "absent", and then the types don't matter. Recall the type of map from above,
\[ (\mathit{pre} · ((γ∘δ) → α) :: (γ ∘ (\underline{\mathtt{list}}\ δ)))
→ \mathtt{list}\ α \]
This is quantified over three type variables. \(γ\) is quantified over mark rows, and \(δ\) over type rows, with \(γ∘δ\) combining them into a row. And \(α\) is quantified over proper types.
Everything before the outermost \(→\) is a row. (Functions in this system are of kind "row → type", not kind "type → type".) It has \(\mathit{pre} · ((γ∘δ) → α)\) as its head, a single field marked present ("pre") with type \((γ∘δ) → α \). \(γ∘δ\) is itself a row. Then for the outer row, the tail \(γ ∘ (\underline{\mathtt{list}}\ δ)\) has the same sequence of marks as the argument to its head, meaning the same number of arguments. \(\underline{\mathtt{list}}\ δ\) is a type row of "apply list to the types in \(δ\)".
Then we might instantiate \(γ\) at \(\mathit{pre} :: \mathit{pre} :: \underline{\mathit{abs}}\), i.e. "two present fields and then nothing". And we might instantiate \(δ\) at \(\mathtt{int} :: \mathtt{string} :: δ'\), i.e. "an int, then a string, then another type row", and \(α\) at \(\mathtt{bool}\). Then we'd have something like the Haskell type
(Int -> String -> Bool) -> [Int] -> [String] -> [Bool]
but it would be rendered in this type system as
\[
(\mathit{pre}
· ((\mathit{pre} · \mathtt{int}
:: \mathit{pre} · \mathtt{string}
:: \underline{\mathit{abs}} ∘ δ')
→ \mathtt{bool})
:: \mathit{pre} · \mathtt{list\ int}
:: \mathit{pre} · \mathtt{list\ string}
:: \underline{\mathit{abs}} ∘ (\underline{\mathtt{list}}\ δ'))
→ \mathtt{list\ bool}
\]
Which, let us say, I do not love. And this kind of thing infects all functions, not just variadic ones! And I don't know how it interacts with partial application. Still, maybe it can be made ergonomic. I think this paper deserves further study, though I'm unlikely to do it myself.
The Zip Calculus
Next is Tullsen, The Zip Calculus (2000, doi: 10.1007/10722010_3). This extends typed lambda calculus to get variadic tuples.
This paper seems to come out of the "program transformation community", which I'm not familiar with. I suspect it's talking about things I know a little about in ways I don't recognize.
The specific typed lambda calculus it extends is "\(\mathrm{F}_ω\)". Fortunately I recently came across the lambda cube so I know how to find out what that means. It's System F, which (as above) is what GHC compiles to as an intermediate step, plus the ability for the user to define their own types, which… I'd always assumed GHC's intermediate System F also had that, but maybe not, or maybe GHC actually compiles to \(\mathrm{F}_ω\)? But… later in the paper it talks about dependent typing, which \(\mathrm{F}_ω\) doesn't have, so maybe the paper is using nonstandard terminology? Argh.
Anyway, I think of System F as a more powerful version of Hindley-Milner, but too powerful to automatically type check, so you need lots of type annotations. If we're making it more powerful I guess we're still going to need those.
I confess I have trouble figuring out what this paper offers in any detail. I think I'd be able to eventually, but I'd need to put in more effort than I felt like right now.
It does give us a short list of functions that, if the language defines them built-in, we can build other functions out of. These are list and what it calls seqTupleL and seqTupleR. These aren't described except for their (identical) type signatures
\[ \mathtt{Monad\ m}
⇒ ×⟨^{i} \mathtt{a}_{.i} → \mathtt{m\ b}_{.i}⟩
→ ×\mathtt{a} → \mathtt{m}(×\mathtt{b}) \]
which I think in Haskell correspond to the types
seqTuple_ :: Monad m => (a1 -> m b1) -> a1 -> m b1
seqTuple_ :: Monad m => (a1 -> m b1, a2 -> m b2) -> (a1, a2) -> m (b1, b2)
seqTuple_
:: Monad m
=> (a1 -> m b1, a2 -> m b2, a3 -> m b3)
-> (a1, a2, a3)
-> m (b1, b2, b3)
If I'm right about that, I'm pretty sure the semantics are "zip the tuple of functions with the tuple of parameters, apply them each in turn and sequence the effects (left-to-right / right-to-left)".
Given these functions, we're specifically told we can implement zip, unzip, map and appF. I'm pretty sure arithmetic, list', appA, puring and trace will be possible, and I weakly guess that printf will be as well, while « and » won't be. I'm not sure about sort or renderCsv.
One thing is that all of these functions are defined with variadic tuples, so that e.g. map would actually be accepted at types like
map :: (a -> b) -> [a] -> [b]
map :: ((a, b) -> c) -> ([a], [b]) -> [c]
map :: ((a, b, c) -> d) -> ([a], [b], [c]) -> [d]
which I assume leaves no room for partial application. It might also be awkward when the final argument needs to be handled separately; I'm not sure if we could get
list' :: [a] -> [a]
list' :: (a, [a]) -> [a]
list' :: (a, a, [a]) -> [a]
or if we'd be stuck with
list' :: () -> [a] -> [a]
list' :: a -> [a] -> [a]
list' :: (a, a) -> [a] -> [a]
Given this limitation, it would be convenient to have variadic curry and uncurry functions,
curry :: (a -> b -> c) -> (a, b) -> c
curry :: (a -> b -> c -> d) -> (a, b, c) -> d
curry :: (a -> b -> c -> d -> e) -> (a, b, c, d) -> e
uncurry :: ((a, b) -> c) -> a -> b -> c
uncurry :: ((a, b, c) -> d) -> a -> b -> c -> d
uncurry :: ((a, b, c, d) -> e) -> a -> b -> c -> d -> e
but no such luck. We're specifically told curry can't be typed, that's an area for future research. And uncurry would break us out of the variadic-tuple paradigm entirely.
I'd be really interested to see a more approachable-to-me version of this paper.
Typeclasses
Finally McBride, Faking It: Simulating Dependent Types in Haskell (2002, doi: 10.1017/S0956796802004355).
I'm happy to say I understand (the relevant parts of) this paper. It adds variadic map directly to Haskell using typeclasses. It then explores further in directions I'm going to ignore. The downside, as PVAP correctly notes, is that you need to explicitly pass in the number of variadic arguments as an initial argument.
The code is simple enough. It felt a bit dated to me: in the past twenty years GHC has added a bunch of new features that seemed like they'd help make it more ergonomic. But I couldn't find a much better way to write it using those, so whatever.
The original is (equivalent to):
{-# LANGUAGE FunctionalDependencies, FlexibleInstances, UndecidableInstances #-}
data Zero = Zero
data Suc n = Suc n
one = Suc Zero :: Suc Zero
two = Suc one :: Suc (Suc Zero)
class ManyApp n fst rest | n fst -> rest where
manyApp :: n -> [fst] -> rest
instance ManyApp Zero t [t] where
manyApp Zero fs = fs
instance ManyApp n fst rest => ManyApp (Suc n) (t -> fst) ([t] -> rest) where
manyApp (Suc n) fs xs = manyApp n (zipWith ($) fs xs)
nZipWith :: ManyApp n fst rest => n -> fst -> rest
nZipWith n f = manyApp n (repeat f)
Here manyApp is the version where instead of just one function, we provide a list of them. The instances give us
manyApp Zero :: [t] -> [t]
manyApp one :: [s -> t] -> [s] -> [t]
manyApp two :: [r -> s -> t] -> [r] -> [s] -> [t]
-- ^ n ^ fst ^ rest
We define it recursively, in terms of its simpler definitions. Then nZipWith is easy to define in terms of manyApp, where it's not easy to define recursively in terms of itself.
So what else can we already implement in Haskell with typeclasses? I think most of my original list of functions, and for several of them I think explicitly specifying the variadic count would be unnecessary.
I tried out a few of them, see here. It's possible there are ways to improve on what I found, but my current sense is:
- Arithmetic,
list, printf: work mostly fine with no variadic count, fine with it.
list': works poorly with no variadic count, fine with it.zip, unzip: need nested tuples, ((a, b), c) rather than (a, b, c). Given that, both work fine with variadic count. zip works poorly without, unzip doesn't for reasons related to the next section.renderCsv: works (mostly?) fine with no variadic count.sort: works okay with one optional argument and no variadic count. With two optional arguments, works fine with something specifying which form you want. (If they're independently optional, there are two two-argument forms, so it wouldn't necessarily be a "variadic count".) But at that point, really, just have different functions.map, appF, appA, puring, trace: work fine with variadic count.», «: do not work.
Here, I consider something to "work" if you can make it do what you want, and work "better" if it doesn't need much type hinting. "works fine" means you don't need type hinting in any places I wouldn't normally expect it in Haskell, and I think the error messages might even be pretty normal?
So I think that with explicit counts, most of these work fine. Without the explicit counts, several of them work pretty okay, but they'll have difficulty if you use them in a weakly-constrained context. Like, print (list "a" "b" "c") won't work because it doesn't know if you want the Show instance on [String] or on String -> [String] or…. (Probably only one of these instances exists, but we can't rely on that.) But then you just need to add a type annotation, print (list "a" "b" "c" :: [String]). list' and zip need a lot more type annotations than is normal, for reasons I maybe have a shallow understanding of but not a deep one.
Partial application
Here's something I think I was vaguely aware of before I started this, but it's clearer now: partial application makes this harder.
Consider the Haskell code
zipWith (\a b c -> a + b + c) [1,2] [3,4]
That uses the existing 2-ary zipWith function, which means it has type [Int -> Int]. (Its value is [(+ 4), (+ 6)].) We could instead have used the existing 3-ary zipWith3, and then it would have type [Int] -> [Int]. If we used a variadic function, what type would it have? All the papers I looked at had some way of answering the question.
In Racket, as far as I know there's no implicit partial application. A function that takes two arguments is different from a function that takes one argument and returns a function that takes one argument. So under PVAP, to choose between the two interpretations, you'd need something like:
(map (λ (a b) (λ (c) (+ a b c))) '(1 2) '(3 4)) ; [Int -> Int]
(λ (cs) (map (λ (a b c) (+ a b c)) '(1 2) '(3 4) cs)) ; [Int] -> [Int]
The Zip Calculus preserves partial application for fixed-arity functions, but not variadic ones. (More precisely, it has partial application for functions but not for variadic tuples.) The two interpretations would be written along the lines of
nZipWith (\(a, b) c -> a + b + c) ([1,2], [3,4]) -- [Int -> Int]
\cs -> nZipWith (\(a, b, c) -> a + b + c) ([1,2], [3,4], cs) -- [Int] -> [Int]
Which is basically the same as the Racket version, apart from syntax.
And "infinitary tuples" has to do something similar. For the list of functions, we'd pass "a function taking a row with two variables and returning a function" as the first argument. For the function on lists we'd pass "a function taking a row with three variables". I guess the system must lose Haskell's equivalence between \a b -> ... and \a -> \b -> ....
The typeclass solution to this is completely different. The inner function is the same for both interpretations, what changes is the initial "variadic count" argument.
nZipWith two (\a b c -> a + b + c) [1,2] [3,4] -- [Int -> Int]
nZipWith three (\a b c -> a + b + c) [1,2] [3,4] -- [Int] -> [Int]
This feels to me like the cleanest of the bunch. I introduced this initial argument as a downside before, but that might be kind of unfair - like, maybe it's only a downside compared to an imaginary world that I hadn't yet realized was impossible.
How else might we solve this problem?
One option is to assume that nZipWith will never want to return a list of functions. I don't love that solution, but here's someone implementing it for appF (which they call liftAn). I haven't checked how well it works.
Something else that might work is to wrap the return value of the initial function in some singleton type.
nZipWith (\a b -> Solo $ \c -> a + b + c) [1,2] [3,4] -- [Int -> Int]
nZipWith (\a b c -> Solo $ a + b + c) [1,2] [3,4] -- [Int] -> [Int]
This is kind of similar to "no partial applications", except you can still do partial applications everywhere else.
And I don't know if this would be possible, but I could imagine using a type annotation to distinguish. If you need to annotate every call to the function, I think I'd rather just specify the number of arguments or something. But if you only need them when it's ambiguous that could be neat.
This isn't a problem for every variadic function. In the previous section, only about half the functions absolutely needed a variadic count, and this is why. (For unzip, it's about the ambiguity in [((a, b), c)]. Do you want to unzip one level to ([(a, b)], [c]), or two to (([a], [b]), [c])?) Other functions had difficulty without the count, but I think that's for unrelated reasons. I think I have a decent intuitive sense of which functions will have this problem and which won't, but I couldn't give a brief description of it. Maybe something to do with matching structures between the initial argument and the rest of the type?
Conclusion
The main thing I take away from this is that I'm basically going to drop variadic functions from my radar for Haskenthetical. Infinitary tuples and the zip calculus don't feel like directions I want to go in. This might affect whether, when and how I add support for typeclasses and various surrounding machinary.
Posted on 02 April 2022
|
Comments
I'm writing this guide for a few reasons. For one, it might be useful to someone, possibly me in future. For two, if I make a mistake, someone might call me out on it and then I can correct it. And for three, it gives me a venue to complain about things I think aren't very good about the online submission form and also our tax system.
(Overall I'm pretty positive on the form! I'm gonna complain a lot, and I'm not going to point out all the places where it works and the instructions are clear and easy to follow. So this will probably come across quite negative, but that's because I'm counting down from perfection, not counting up from zero.)
Most people in the UK don't have to file one of these. I started filing them when I started earning in the 40% tax bracket. I'm not sure I still have to - I think I got a message a year or two back saying I could stop - but if I don't I'll pay more tax than I need to.
HMRC publishes a document called "how to fill in your tax return". (In previous years it had the reference SA150, and that's still in the filename, but it's no longer written under the title for some reason.) I actually haven't found it very helpful, it mostly doesn't seem to answer questions that the website leaves me with. But I guess it might be helpful in theory.
Update December 29: I only know about the parts of this process that are relevant to me. Some questions about other parts are answered in the comments on /r/UKPersonalFinance. Also, I generally find that community to be very helpful and knowledgable, so I find it reassuring that they only caught one mistake so far.
The gov.uk page on filing says you have to register first unless you sent a tax return last year. I've sent tax returns for several years running now, and I don't remember what registering was like.
Logging in from there I get sent to my "personal tax account" page and click the "complete your tax return" link in the top right box. I feel like that was harder to find in the past. It explains who can and can't file a return, I assume I read that in a previous year and could then and still can, and I click 'start now'.
The first page has a bunch of stuff filled in for me, mostly accurate.

"P J" is my first two initials, not my first name, but nice try. The all-caps HAZELDEN seems unnecessary, you don't need to worry about my handwriting.

These say 'optional', which sounds like I don't need to give them if I don't want to. But up above it says
'Optional' indicates only complete if relevant to you
So maybe that means "give us this if you have one"? I'm probably safe to leave out my phone number, I don't want them calling me and I don't know what "STD" means. I'll grudgingly give them my email address I guess.
For years I've been using my parents' address for all official stuff, which is easier than telling banks and the like every time I move house. But some time this year I got a scary letter telling me I had to register for the electoral roll in my current place, which meant I got removed from it back in Bristol. So probably I have to give my current address here too.
(I don't see why it's any of the government's business where I live. Unfortunately they disagree, and they have all the power in this relationship.)

Well this is awkward. I moved in here in 2019, but I wouldn't have given this address when filling in my 2019-20 tax return. Will they get pissy with me if I give the date I moved in? Eh, probably not.
Almost every address form I've filled in for the past several years has let me give my postcode and then select my exact address from a short dropdown, or enter it manually. This address form does not offer that.
There's no dropdown box, even if I select "Abroad". Also, this is still supposed to be asking about my address - "where the income was earned" is a different question. (And not a very clearly worded one, what if I earned income in multiple countries?) Fortunately I have never lived or earned income outside the UK.
"The postcode must be in capitals." Well done for finding and documenting a bug, HMRC, but I feel like it shouldn't be too hard to fix this one.

Residency is "based on whether you lived in England and Northern Ireland, Scotland or Wales for the majority of the tax year". I assume they mean "plurality", but maybe if you spent less than half the year in any of these, you don't pay tax at all. (Tax collectors hate him! Nonlocal man discovers one weird trick…)
That's not what "e.g." means, but the date is correct.
This is 'optional', so maybe there are people who don't have a marital status, as distinct from having the marital status 'single'? Or maybe, contra what they said above, it means I don't have to tell them, and then probably they'll treat me as single if I don't specify?
The options are: Single, Married, In Civil Partnership, Divorced, Civil Partnership dissolved, Widow, Widower, Surviving Civil Partner, Separated. Obviously you can be more than one of these in any given tax year, or even more than one of them simultaneously, so the help text is not very helpful. I guess the idea is you give the most specific version of the most recent change as of the end of the tax year? I don't know who would ever pick "separated". Luckily for me, the government hasn't decided it cares about long-term cohabiting relationships until we actively make them legible, at least not for tax purposes. So I get to just say "single" and not worry about it.
This is the only part of the tax return (at least the pages I saw) where your gender becomes relevant, and then only for widows and widowers. I don't know what the nonbinary version is, but they get left out.

If they're assuming I didn't move house, you'd think they could assume I didn't go blind or get a blind spouse or civil partner.
I wonder what counts as an "other register". I think it's a crime to lie on my tax return, and quite possibly a crime to lie to my local authority about being blind. But it might not be a crime to lie on Honest Joe's Register Of Definitely Actually Blind People, and then to truthfully tell HMRC that I'm on that register. (This sounds like the sort of thing that you patiently explain to a judge and then the judge adds a little extra to your fine for being a smartarse. You try to appeal and the appeals court rejects with the comment "lolno". If you're going to try this, I think the funniest way would be to borrow a guide dog to take to court with you, maybe carry a cane slung over your shoulder, but make no actual pretense at blindness.)
There's nothing here telling you how to figure out if you're on plan 1 or plan 2, but I am indeed on plan 1. The Student Loan Company told them that (according to the help text), but apparently didn't tell them enough to know that I do not have and am not repaying a postgrad loan.
The next page helps figure out which other pages should be included in the rest of the form, and which ones can be skipped.
In my case, I was an employee (or director or office-holder) during the tax year, so I answer yes and tell them how many employments (or directorships) I had (one) and the name of the employer.
I wasn't self-employed or in a partnership, but if I was I'd need to tell them how many of those I had and their names, too. I didn't get income from UK land or property over £1,000 (or indeed at all), I didn't receive any foreign income, and I don't need to complete the capital gains section.
For capital gains it's not entirely obvious that the answer is no. Here's the advice:
You must report your capital gains and attach your computations if in the tax year either:
- you disposed of chargeable assets which were worth more than £49,200
- your chargeable gains, before the deduction of any losses, are more than £12,300
- you have gains in an earlier year taxable in this period
- you want to claim an allowable capital loss or make any other capital gains claim or election for the year
In working out if the assets you disposed of were worth more than £49,200 use the market value of any assets you gave away or sold for less than full value and ignore disposals of:
- exempt assets such as private cars, shares held within Individual Savings Accounts
- assets to your spouse or civil partner, if you were living together at some time during the tax year
- your own home where: [omitted a sub-list because I don't even own a home]
In working out your total chargeable gains include any gains attributed to you, for example, because you're a settlor or beneficiary of a trust, or in certain cases where you're a member of a non-resident company.
This is fairly readable, but it keeps using words like "chargeable" and "allowable". Those sound like they have important technical definitions. Are we given the important technical defintions? Ha, no.
So here's my current understanding. I have shares in some index funds in ISAs and pensions, but I'm pretty sure I should ignore those. And I own a handful of individual stocks and cryptocurrencies, not in tax-protected accounts, that I shouldn't ignore.
But so far all I've done is buy things and let their values go up or down. I haven't "disposed of" any of them: sold, traded or given away. That means I don't need to worry about it. When I dispose of something, I'll need to work out how how much profit or loss I made on it, and also (as a separate question) how much it was worth at the time. If those amounts go over certain thresholds in total for the year (£12,300 and £49,200 respectively), then I need to fill in the capital gains section. And there's also another two reasons I might need to, but I'm confident those don't apply to me either.
So I can answer "no" to capital gains because I haven't disposed of anything. Also, outside of ISAs and pensions I had less than £49,200 and my on-paper gains for the year were less than £12,300, so I could answer "no" even if I'd sold everything at the end of the year.
(Also, something unclear: to calculate gains, the obvious thing is to take "price when disposed of" and subtract "price when bought". And we're calculating "price when disposed of" anyway. But we're told to ignore certain disposals when calculating the total disposal price. Do we also ignore those disposals when calculating gains? I would guess so, but mostly I'm glad I don't have to worry about it.)
The next page is the same sort of thing, but in my case less clear.

An important detail here is that you can omit interest earned in an ISA. Nothing on the page says so. You might think that if you only earned interest in an ISA, you say here that you earned interest, and later you tell them it was only in an ISA. At any rate, that's what I thought the first time. But then they told me I owed tax on all that interest, so I decided to go back and tell them I didn't earn any interest.
I guess that was lying on my tax return, and I just admitted to a crime? Thanks, HMRC.
(I just double checked: if I say I did earn interest, I get a new page where they ask me about "interest that's already been taxed", "interest that hasn't yet been taxed", and "foreign interest that hasn't yet been taxed". There's nothing on that page, either, saying I can omit ISAs.)

Similarly, dividends earned in an ISA don't count here. I did not earn any dividends outside of an ISA last tax year. (This tax year I've earned about £1.50 of them so far.)

Ever get the feeling that someone said "every question needs help text" and the person writing the help text was phoning it in?
I don't know how Child Benefit works. Is anyone in the position of "I got it during the tax year starting on 6 April 2020, but the payments had stopped before 6 April 2020"?

This seems to be an "if you made a mistake, that's fine, you can correct it now" thing. I appreciate that.

This help text is long so I'm not including it. This includes casual earnings, and I might have had some of those? Certainly I have in other years, like the money I sometimes got for getting my brain scanned. But it says I don't need to report if the total from this plus self employment is less than £1,000, which it is for me.
They don't mention gambling income, and mine isn't that high anyway, but I think that should be excluded.

I don't know what these are and the help text doesn't help much, but probably not.

Again, long help text. But the gist seems to be that if I have more than £1,073,100 in pensions in total (5 significant digits! Impressive precision), or if I (or my employer) put more than £40,000 into pensions this year, I need to worry about this. Neither is the case for me. (Yet! Growth mindset.)
One more page of basically the same thing, but this one is easy again. Yes, I contributed to a personal pension. Yes, I gave to charity (and claimed gift aid). My partner and I are ineligible for married couple's allowance (we are neither married nor in a civil partnership, and anyway we were both born after 6 April 1935). Nor can I transfer 10% of my personal allowance to them (we are neither married nor in a civil partnership). I don't want to claim other tax reliefs. I don't have a tax adviser. I… think I haven't used any tax avoidance schemes, but that probably relies on distinguishing between schemes that HMRC thinks are legit (like giving to charity) and schemes that HMRC thinks are kinda sus. I haven't used any disguised remuneration avoidance schemes. I am not acting in capacity or on behalf of anyone else.
There is one interesting one here.
I got a tax rebate in tax year 2019-20 from 2018-19, and then another in tax year 2020-21 from 2019-20. I think neither of these is what it's asking about. Rather, I think this is asking about rebates in tax year 2020-21 from tax already paid in that tax year.
Having filled in those three pages, I get an overview page listing what I've filled in so far and what I still need to do. The first thing to do is income. I only had one employer this year, so I only have one section for that.
They start with the company name, that I already gave them but I can change it now if I want I guess. After that, the next three questions are answered by my P60, which I was able to find because my employer emailed it to me.
These last two are "optional". First time I did this, I thought that meant "we have a copy of your P60 too, so if you don't fill this in we'll fill it in for you". Nope, it means "if you don't fill this in we'll think it's 0".
Then they want to know if I got any tips or other payments not on my P60, which I didn't. This one is optional too - if I try to enter 0 it complains and tells me to leave it blank.
Also, some helpful Javascript on the page makes sure your numbers are given to two decimal places, i.e. pounds and pennies. You can't enter pennies, they'll be truncated (£567.89 becomes £567.00), but it makes sure to show you them.
They also want to know if I was a director (no) and something about "inside off-payroll working engagements" (not entirely clear what this is, but no).
I did have benefits, medical insurance. The value of that will be on my P11D, not my P60, but they don't ask for it here. That's on the next page, which I guess I won't get shown if I didn't have any?
The final question almost caught me out:
I don't normally think of myself as having employment expenses. But I've been working from home, and this is how I claim back some of my utility bills.
My answers to that question added two new pages that weren't listed on the overview before. First for taxable benefits and expenses, listed on my P11D. I have an email copy of that too, I just copy the amount listed for medical insurance on that into the "private medical or dental insurance" box on the page.
They even tell me which number to use. (I have three, "cost to employer", "amount made good or from which tax deducted" and "cash equivalent". The middle one is £0 and the others are equal, so it's not hard for me. But if the middle one wasn't £0, I wouldn't be sure whether to use "cost to employer" or "cash equivalent" - but the latter is the one labeled with an "11", so that's the one to use.)
Then there's a page for expenses not reimbursed. The weirdly specific thing on this page is the box for "fixed deductions for expenses":
Based on the (long) help text, this seems to be "people in certain jobs and industries get to put specific numbers here, regardless of what their actual expenses were". (But they can choose to instead put their actual expenses in another box.) But if you're "a uniformed airline or helicoptor pilot, co-pilot, flight deck crew or cabin crew", you get a different box to put specific numbers in.

But as far as I know I do not work in such a job or industry. The only question relevant to me is "other".
The help text doesn't make it clear how much I can claim, but the link mostly does. I can claim for gas, electricity, metered water, business phone calls and dial-up internet; but only the amount of them that's related to my work. So I guess I should figure out how much higher my bills are WFH than they would be if I was in the office?
I can claim up to £6/week without evidence, or more with evidence. I can only claim if I have to work from home, not if I do so by choice. I had to look this up, but there were four months where my office was closed (April, May, June and November), so call it 16 weeks. It's also not entirely clear whether that's "£6/week no matter how much I had to work from home that week" or whether I should think of it as £1.20/day, but that doesn't affect me personally. I assume I shouldn't count any holidays I took, but I don't think I took any in those months.
Same-day update: Reddit user pes_planus points out that if you had to work from home for a single day due to Covid, you can claim for the whole year. At £6/week, that's £312 in total. This is the case for both 2020-21 and 2021-22.
Following this page there's one for providing any more information.

I'm not sure what kind of thing I'd need to use it for, but I don't have anything to add. Which is good because it's kind of embarrassingly limited. I'm not allowed to use multiple lines or most punctuation?!
Next up is pensions. I have two pensions that I contributed to this year, my employer one and an SIPP. I'm not aware of having a retirement annuity contract whatever one of those is, and I don't have any overseas pensions, so there are only one or two questions relevant to me. Still, this page is frankly confusing.

I have a standing order to deposit into my SIPP every month, and then about 11 weeks later, 25% of that amount gets added as tax relief. (It's supposed to be 6-8 weeks, but it's not.) So do I count the tax relief in the tax year when it arrived, or the tax year when I deposited the money? So far I've been doing when I deposited, and that's what they suggest by telling me to multiply the amount I contributed by 1.25. On the other hand, if that calculation is always correct, why don't they save me the trouble and do it for me? (Maybe they expect me to have a document somewhere giving the total amount?) In any case, there's nothing saying explicitly what to do. It probably doesn't make that much difference as long as I'm consistent year-on-year, so let's stick with "deposited".

Meanwhile, my employer pension has two sources of contributions. There's the stuff "my employer pays", which doesn't get written on my payslip, and the stuff "I pay", which does. These are both part of my compensation package, but I think we like to pretend that if my employer doesn't write it on my payslip it's not causing me to get paid less? And we make things more complicated and less transparent in service of this fiction.
Anyway, the stuff "my employer pays" I think isn't relevant here. The stuff "I pay" is. In my case, this is also paid relief at source, meaning it's deducted after I've paid tax on it. So that sounds like it matches "Payments to your employer's scheme which were not deducted from your pay before tax". Buuut… I think that question is trying to ask about payments which were expected to be deducted before tax. At my previous job that's how it happened, and it sounds like under certain circumstances that could have gone wrong and then I'd use this question to correct that.
So I think contributions "I paid" to my employer pension actually go along with my SIPP contributions as the answer to the first question, and I leave this one blank. (It's not marked optional, but it doesn't accept 0.)
For charity, there's three questions that look maybe relevant.

For pensions I needed to figure out my contribution plus what was added, for charity I just need to give my own contribution. Obviously. Still, this number is easy to find in my records.

I think this is a roundabout way of asking how much gift aid I expect to donate in tax years 2021-22 and/or 22-23? They'll assume it's the amount I donated this year, minus whatever I put here. And then they'll adjust my PAYG tax code for that, to reduce overpayments.
Most of my charity donations were monthly recurring, but that left me slightly below my "10% of take-home" target, so I did do a one-off donation on top of that which I don't particularly expect to repeat. (But I haven't checked how far below my target I am right now.) But I do expect to donate more in total this year, so I'm going to leave this blank.

Not much help about what specific countries count as "certain" here, or what the definition of charity is for tax purposes. Some of the money I donate goes to MIRI, which is not a UK charity. But it goes via EA Funds, which is. So I'm pretty sure I haven't officially done this.
I can ignore the rest: I'm not asking to treat any payments as being made in a year other than they were actually made; and I haven't given any shares, securities, land or buildings to charity.
The next three pages are about my "PAYE Notice of Coding". They never say what one of these is, but it seems to be a letter they send out, that as far as I can see doesn't contain the words "PAYE" or "notice of coding". (It does say "your tax code notice", which is at least similar.)
Awkwardly, I can't find one more recent than 2018-19: not in my physical documents box, my "I should look through these documents at some point" pile, or my email. I'm sure I've had them more recently, so, um. They don't tell me what to do in this situation, but I guess presumably I can ask them for a new one? But… look at these questions.
The first is "does this number match what's on your coding notice?"
It's not clear whether it's talking about 2019-20 or 2020-21. If I had to guess - and I suppose I kind of do? Then I'd guess it's asking about underpaid tax from 2019-20 and earlier that I should have paid back in 2020-21 through my tax code for 2020-21.
The second is also "does this number match what's on your coding notice?" I think the difference is that last one was talking about underpaid tax from previous years, and this one is talking about underpaid tax from 2020-21 that's already been put on my 2020-21 tax code.
(For these, if I select "no" I get a space to put a different number and a space to tell them where that other number comes from.)

The third question doesn't look like the first two, although it does in the linked video and the help text sounds like it should. It's another "does this number match what's on your coding notice?" This time it's about… outstanding debts other than underpaid tax? What else might I owe to HMRC?
So, okay. I confess I don't really know what's going on with any of this. But suppose I ask HMRC for a replacement Notice of Coding. Are they really going to give me a letter telling me a different number than they have on the website? If so, why not just take that number from wherever they got it for the letter, and put it on the website themselves?
Plus, I've received tax refunds the last two years running, which seems like a weird thing to get if they think I owe them money?
So I think I'm just gonna assume these are all £0.
The three linked videos are short (1:15 to 2:07), but they don't add much that's not in the help text, and I'd much rather they be presented as "text with embedded images" or even just plain text. At least they have subtitles.
Nearly done! Quickfire round.
The next page is one I can't do anything with until after I've submitted the return. This seems like a strange place for it.

Then we get a page about my student loan, which doesn't even have a help text. This is on my P60 again, and also I have it in my own records and I'm pretty sure on a letter somewhere.

Next they have two questions about underpaid tax.
The first is: if it turns out I didn't pay enough tax last year (2020-21, the year I'm filing for), do I want to pay it back through my tax code for next year (2022-23)? i.e. to get it automatically deducted from my payslip starting April 2022? That seems reasonable, sure. If I say no I have to pay it directly by January 2022. I think it's more likely I paid too much, but gonna say yes anyway.
I can only do this if I file by 30th December, which is (checks calendar) soon. I guess if this guide does turn out to be useful to someone, they won't be able to take advantage of this, this year.

The second is: if they think I'll owe tax this year (2021-22, the unfinished year I'm writing this), do I want it put onto my tax code for… also this year? But this doesn't apply to tax on employed earnings (i.e. the only thing I think I owe tax on) or pensions. Also they apparently think 5 April 2022 gets the past tense.
So, no, because I don't think I'll owe the relevant kind of tax, and if they decide I probably will that's going to confuse things. And no again, because if they decide I'll probably owe something, putting it on my tax code for this year (with three payslips to go) also seems like it's going to confuse things. Certainly it'll make updating my ledger mildly less convenient. If I was going to do this, I'd rather it go on my tax code for next year, like with the previous question.
If I want to make "adjustments" I can do that, but I don't think it applies. (It sounds like these adjustments might be mostly "pretending things happened at different times than they actually happened"?)

The help texts all include "An entry will only be required in limited circumstances", and make it sound like calculating the amounts to go in these boxes is kind of complicated, so I'm glad I don't have to think about them.
If I used provisional figures (I didn't) I give them details about those, and then finally there's a space for "anything else we should know" with the same restrictions on length and punctuation as before. Also I can attach a document if I want.


That's the last thing to fill in. Next there's a page where they repeat some of the things I said back to me, to confirm, and then a page to show me my tax calculation. Initially it just says how much they owe me (or presumably, how much I'd owe them, if that was the case). But then there's also a page showing the full calculation, which I find super valuable for understanding how it all fits together and double checking that I haven't made any mistakes.
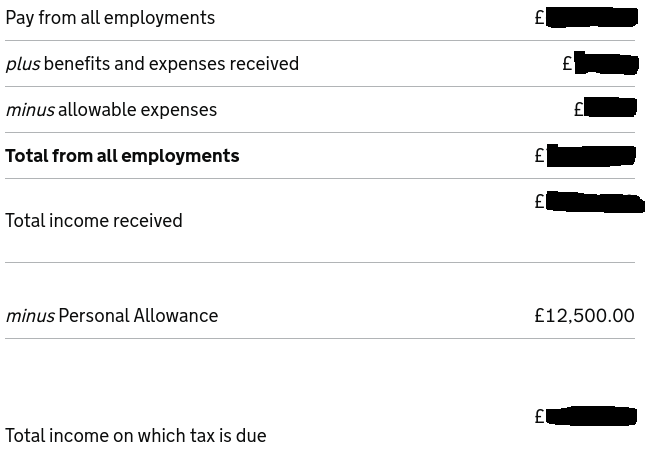
The top three numbers here come directly from my return, and Personal Allowance is the same for most people, £12,500 for 2020-21. (If you earn over £100k it starts to decrease, giving a marginal 60% tax band in between two marginal 40% tax bands. I guess it was politically easier to raise taxes this way than to raise them in some more sensible way?) The rest are just adding and subtracting those numbers in the obvious way.
Normally, of the "income on which tax is due", I'd pay 20% on the first £37,500 and 40% on the rest. But

The pension number is the amount I put in the first pension box above, "payments to registered pension schemes". That was money I'd paid into my pensions, plus tax relief I'd been given for it.
The charity number is the amount of gift aid payments I made, times 1.25, because the number I entered didn't include tax relief. (That tax relief went to the charities, not to me.)
The idea with these is that money I put into pensions, or give to charity, is money I don't have to pay tax on. So they make two adjustments for it:
-
Return 25% of the money I deposit/donate, to me (for pensions) or the charity (for charities). This happens without needing to fill in a tax return. For those in the basic rate tax bracket, it gives the right amount - £100 pre-tax becomes £80 post-tax, so later we turn the £80 back into £100.
-
For higher rate taxpayers, also move some money from the "pay 40% tax" bucket to the "pay 20% tax" bucket. £100 pre-tax becomes £60 post-tax, which (from the previous point) becomes £75 when moved to the pension pot or charity. So they move £75 between buckets, and instead of paying £30 on that I now pay £15. So of the original £100, I now have £15, the charity has £75, and HMRC has £10. This is the same as me giving the charity £75 pre-tax and then paying 40% tax on £25, so it works out fine, but man I find this math confusing.
If I actually want to give £100 pre-tax, I still need to give the charity £80. They'll claim back £20 and so will I, so I'll have given them £100 pre-tax and paid 40% tax on £33.33. Alternatively I can take the £15 I got returned from £60 and redonate that, becoming £18.75 to the charity, then also donate the £3.75 I get returned from that, and so on - in the limit, this works out as the charity having £100 and myself and HMRC having £0 each.
(When HMRC shifts money between buckets, a higher-rate taxpayer can become a basic-rate taxpayer. I assume the math still works out fine at the boundaries? I haven't checked though.)
And so we have these calculations:

I'm not sure why "Income Tax due after allowances and reliefs" comes before "Income Tax due", but since I don't have any allowances or reliefs the numbers are the same for me. I assume student loan repayments would be different from £0 if the wrong amount had been automatically taken from my payslips.
Now I get to download a PDF copy of what I just filled in, formatted on what I guess is a copy of the paper form I'd use if I wasn't doing it online. And then right before I submit, two more checkboxes to tick:
This first one seems less helpful than it might be, failing to distinguish "oops I did this wrong" from "I didn't need to do this". I guess they don't want to confuse non-mathematicians who didn't have any coronavirus support payments, and it still works as a reminder.
I think after I click "submit" on this page, I'll enter my password again and be finished. But I haven't done that yet - I'll wait to see if anyone wants to tell me I did something wrong, first.
Update December 29: Yep, that was it. There was a "submitting" spinner for about 30 seconds, and then

Woop! It takes up to 72 hours to process and I can make corrections in that time. But assuming I don't realize I have any of those, I'm done. At some point they're going to send me back the money I overpaid, historically that's gone into my bank account but I don't remember if I've had to do anything particular to make it happen. Certainly it wasn't very involved if I did.
They give me a "submission receipt reference number", which looks like 32 digits in base 36 (numbers and uppercase letters, mine includes Z, I and O so probably all letters are possible). Sounds like it's a hash of the contents of my return, with a signature so that no one else can generate a valid one. Neat. It's also included in the PDF copy I downloaded earlier.
I assume it's not intended to be confidential, but they don't say it's safe to share, so I won't.
Posted on 28 December 2021
|
Comments
A megasecond, one million seconds, is 11 days and 14 hours. (13 hours, 46 minutes and 40 seconds, assuming no leap seconds.) About a week and a half.
Ten megaseconds is 116 days. (115, plus 17:46:40.) A bit less than four months, a third of a year.
A hundred megaseconds is 1,157 days. (Plus 9:46:40.) Roughly three years and two months - it could be 61 or 62 days depending on leap years.
I think it might be kind of nice if we celebrated a hundred megaseconds additonally-to and/or instead-of birthdays.
One thing I like about it is that humanity won't stay on Earth forever. If we go interplanetary, I think we're more likely to keep measuring time in seconds than in Earth years. I like this as a way of looking to the future.
Another thing is, it doesn't happen at the same time every (Earth) year. Some birthdays fall on or near holidays, or during seasons we don't much like, and that can make them less convenient to celebrate. If that happens to you one hundred megaseconds, it probably won't happen the next hundred megaseconds. (I think a five month offset would be better than two for this purpose, you'd never be in the same season twice in a row, but two is better than zero.)
I also just think it's kind of a sweet spot time interval? I'm old enough now that years don't feel very long, decades do, and a hundred megaseconds is nicely in between.
(If "hundred megaseconds" is unwieldy, a quick look at wikipedia suggests "yisec" from Chinese or "okusec" from Japanese. Or maybe "myri-myri-sec" from Ancient Greek. I think my favorite would be "hecto-megasec" from Ancient Greek via SI. I'm not going to try to use any of these myself though.)
Ten hundred megaseconds, a billion seconds, is 11,574 days. About 31 years eight months. (The remainder is 251-253 days, depending on leap years. Plus 1:46:40.) That's how old I turned on August 21st this year.
I didn't do anything to celebrate, partly because even though I'd put it in my calendar a long time before, I didn't remember until a couple days after, and partly because I'm not very good at celebrating things. (I don't normally celebrate my birthdays, either.) I did do some work on Haskenthetical for the first time in months, which feels like a good start to the next billion. Maybe I'll celebrate turning eleven, which will be on October 21st, 2024.
If you're interested, here's a widget you can use to calculate your age, or other intervals, in hundred megaseconds.
Thanks to Miranda for comments.
Posted on 20 September 2021
|
Comments
(Content note: minor spoilers for Harry Potter and the Order of the Phoenix.)
Scott Aaronson writes about blankfaces,
anyone who enjoys wielding the power entrusted in them to make others miserable by acting like a cog in a broken machine, rather than like a human being with courage, judgment, and responsibility for their actions. A blankface meets every appeal to facts, logic, and plain compassion with the same repetition of rules and regulations and the same blank stare—a blank stare that, more often than not, conceals a contemptuous smile.
I want to push back against this a bit.
First, one of the defining aspects of blankfacedness is their internal experience. It's someone who enjoys wielding their power. This is a very hard thing to judge from the outside.
I used to work in a cinema. One day a mother came in with her young child, perhaps fivish years old. She was late for a busy screening, and the person selling tickets warned they might not be able to sit together. She said that was fine, bought popcorn and went in. Soon afterwards she came back out, complaining that they couldn't sit together. She wanted a refund for the tickets (fine) and popcorn (not fine, but she insisted). The conversation between her and my manager escalated a bit. I don't remember who brought up the police, but she at least was very confident that she knew her rights and the police would back her up if they arrived. Eventually he gave her a refund.
If it had been up to me? And if I hadn't had to worry about things like PR and "someone yelling in the lobby would ruin the experience for people watching movies"? I think I would absolutely have used the "no, sorry, those are the rules" move. I would have been happy to do so. Does that make me a blankface? But it's not that I would have enjoyed wielding my power as such. Rather it's that I would have enjoyed punishing her, specifically, for acting in ways that I endorsedly think are bad to act in.
Does someone's internal experience matter, though? If they act a certain way, should we care how they feel? I think we should, and if we don't we shouldn't make claims about it.
That is, if what you care about is whether someone is acting a certain way, then don't mention enjoyment when you define a blankface. And if you really do care about the enjoyment part of it - well, how do you know what someone is feeling and why?
I predict that if the term "blankface" takes off, no matter how much people defining the term emphasize the "enjoys" part of it, people using the term will not be careful about checking that. Partly I think this because Scott wasn't: in two of his examples, he accused people of being blankfaces whom he'd never interacted with and could not identify. Does he really think that a web portal was badly designed out of malice? But also I think that… like, even if you can tell that someone is just acting a certain way because they enjoy it, even if you're really sure that's what's going on, you won't properly be able to capture that in your description of the events. So people will read a story where it seems like the thing making them a blankface is the way they acted, and then they'll tell their own similar stories where people acted in similar ways, and they'll use the term "blankface".
There's a lot of potential here for a kind of (reverse?) motte-and-bailey, where the bailey is "I'm calling someone a blankface which is explicitly defined as having an enjoyment part to it", and the motte is "…but no one uses it that way, so obviously I didn't mean to imply that I know what was going on in their head".
Here's another reason someone might externally act blankfacedly: fear. Yes, this is ridiculous, but if I admit that out loud I'll be seen as undermining my boss who already has it in for me, so…. Or, exhaustion: this is the third sob story I've heard today. I cannot deal with feeling more sympathy.
Given how strongly Scott feels about blankfaces (they've apparently dehumanized themselves and deserve no mercy), I certainly hope he cares whether they act blankfacedly for sympathetic or unsympathetic reasons. And if we're to care about that, I think we have to admit that most of the time we don't really know.
Second and relatedly, I think we should distinguish between "this person is blankfacing" and "this person is a blankface". Like, maybe someone right now is enjoying wielding petty power for the sake of it. I don't currently predict that that person routinely enjoys acting that way, or enjoys acting that way in every situation where they have petty power. That's maybe not much consolation to their victim right now, but still.
Perhaps I should predict that? But I currently don't, and Scott gives me no reason to.
Third, I'm not sure Umbridge is an example of the archetype. Or, if Umbridge is really what Scott wants to point at, I'm not sure his explicit definition matches up.
The most despicable villain in the Harry Potter universe is not Lord Voldemort, who's mostly just a faraway cipher and abstract embodiment of pure evil, no more hateable than an earthquake. Rather, it's Dolores Jane Umbridge, the toadlike Ministry of Magic bureaucrat who takes over Hogwarts school, forces out Dumbledore as headmaster, and terrorizes the students with increasingly draconian "Educational Decrees." Umbridge's decrees are mostly aimed at punishing Harry Potter and his friends, who've embarrassed the Ministry by telling everyone the truth that Voldemort has returned and by readying themselves to fight him, thereby defying the Ministry's head-in-the-sand policy.
Anyway, I’ll say this for Harry Potter: Rowling's portrayal of Umbridge is so spot-on and merciless that, for anyone who knows the series, I could simply define a blankface to be anyone sufficiently Umbridge-like.
Spoilers: the educational decrees are not the extent of Umbridge's villainy. She also sends dementors to attack Harry and his cousin. She tries to slip Harry a truth serum, and later tries to force-feed it to him. When she can't do that, she tries to torture him. None of this is legal, some of it is super-duper illegal, and her superiors aren't pressuring her into it. Umbridge doesn't simply act like a cog in a broken machine. She exercises judgment, and I think even some courage, in service of villainous ends.
(I am not, here, describing Umbridge's motivations. I think I have some idea of what they are, but I'm not sure I'd capture them very well and my feeling is they're not super relevant for this bit.)
However annoyed Scott may be at his daughter's lifeguard, I predict that describing the lifeguard as Umbridge-like is unfair. I predict, for example, that she would never take initiative to deliberately engineer a situation in which Scott's daughter nearly drowns.
I think Scott is pointing at something true, and important to know about. But I think he's conflating a few different things (blankfacing-regardless-of-internal-experience, blankfacing-specifically-meaning-enjoying-it, being-a-blankface, Umbridge), and I worry that the way he's pointing at them will result in bad discourse norms. I still think it's good that he published, but I don't think that essay is the ideal version of what it could be, and I'm trying here to point at ways I think it falls short.
Posted on 08 August 2021
|
Comments
This review originally appeared on the blog Astral Codex Ten as part of a contest. You can now read it here, with working footnotes. There's even an audio version as part of the ACX podcast; the footnotes are all read out at the end.
Shasta County
Shasta County, northern California, is a rural area home to many cattle ranchers. It has an unusual legal feature: its rangeland can be designated as either open or closed. (Most places in the country pick one or the other.) The county board of supervisors has the power to close range, but not to open it. When a range closure petition is circulated, the cattlemen have strong opinions about it. They like their range open.
If you ask why, they'll tell you it's because of what happens if a motorist hits one of their herd. In open range, the driver should have been more careful; "the motorist buys the cow". In closed range, the rancher should have been sure to fence his animals in; he compensates the motorist.
They are simply wrong about this. Range designation has no legal effect on what happens when a motorist hits a cow. (Or, maybe not quite no effect. There's some, mostly theoretical, reason to think it might make a small difference. But certainly the ranchers exaggerate it.) When these cases go to court, ranchers either settle or lose, and complain that lawyers don't understand the law.
Even if they were right about the law, they have insurance for such matters. They'll tell you that their insurance premiums will rise if the range closes, but insurers don't adjust their rates on that level of granularity. One major insurer doesn't even adjust its rates between Shasta County and other counties in California. They might plausibly want to increase their coverage amount, but the cost of that is on the order of $10/year.
No, the actual effect that range designation has, is on what happens when a rancher's cow accidentally trespasses on someone else's land. In closed range, the owner is responsible for fencing in his cattle. If they trespass on someone else's land, he's strictly liable for any damage they cause. In open range, the landowner is responsible for fencing the cattle out; the cattle owner is only liable for damages if the land was entirely fenced or if he took them there deliberately. (Law enforcement also has more power to impound cattle in closed range, but most years they don't do that even once.)
The cattlemen mostly don't understand this detail of the law. They have a vague grasp of it, but it's even more simplified than the version I've just given. And they don't act upon it. Regardless of range designation, they follow an informal code of neighborliness. According to them, it's unneighborly to deliberately allow your cattle to trespass; but it's also unneighborly to make a fuss when it does happen. The usual response is to call the owner (whom you indentify by brand) and let him know. He'll thank you, apologize, and drive down to collect it. You don't ask for compensation.
Or, sometimes it would be inconvenient for him to collect it. If his cow has joined your herd, it's simpler for it just to stay there until you round them up. In that case, you'll be feeding someone else's cow, possibly for months. The expense of that is perhaps $100, a notable amount, but you still don't ask for compensation.
Sometimes a rancher will fail to live up to this standard of neighborliness. He'll be careless about fencing in his cattle, or slow to pick them up. Usually the victims will gossip about him, and that's enough to provoke an apology. If not, they get tougher. They may drive a cow to somewhere it would be inconvenient to collect - this is questionably legal. They might threaten to injure or kill the animal. They might actually injure or kill it - this is certainly illegal, but they won't get in trouble for it.
They almost never ask for money, and lawyers only get involved in the most exceptional circumstances (the author found two instances of that happening). When someone does need to pay a debt, he does so in kind: "Should your goat happen to eat your neighbor's tomatoes, the neighborly thing for you to do would be to help replant the tomatoes; a transfer of money would be too cold and too impersonal." Ranchers do keep rough mental account of debits and credits, but they allow these to be settled long term and over multiple fronts. A debt of "he refused to help with our mutual fence" might be paid with "but he did look after my place while I was on holiday".
(This is how ranchers deal with each other. Ranchette owners will also sometimes complain to public officials, who in turn talk to the cattle owner. They'll sometimes file damage claims against the rancher's insurance. It's ranchette owners who are responsible for range closure petitions.)
Range designation also doesn't affect the legal rules around building and maintaining fences. But it does change the meaning of the fences themselves, so maybe it would change how cattlemen handle fencing? But again, no. Legally, in some situations neighbors are required to share fence maintenance duties, and sometimes someone can build a fence and later force his neighbor to pay some of the cost. The cattlemen don't generally know this, and would ignore it if they did. They maintain fences unilaterally; if one of them doesn't do any work for years, the other will complain at them. If they want to build or upgrade a fence, they'll talk to their neighbor in advance, and usually figure out between them a rough way to split the material costs and labor in proportion to how many cattle each has near the fence. (Crop farmers aren't asked to pay to keep the ranchers' animals out.) Occasionally they can't reach an agreement, but this doesn't cause much animosity. This is despite that fences cost thousands of dollars per mile to build, and half a person-day per mile per year to maintain.
So this is a puzzle. Range designation is legally relevant with regard to cattle trespass, but it doesn't change how ranchers act in that regard. Range designation is not legally relevant to motor accidents, and ranchers have no reason to think it is; but that's why they ostensibly care about it.
(And it's not just words. Many of them act on their beliefs. We can roughly divide cattlemen into "traditionalists who don't irrigate and can't afford fences" and "modernists who irrigate and already use fences" - by improving pasture, irrigation vastly decreases the amount of land needed. After a closure, traditionalists drop their grazing leases in the area. Modernists oppose closures like traditionalists, but they don't react to them if they pass.)
What's up with this? Why do the cattlemen continue to be so wrong in the face of, you know, everything?
What's up with this?
Order Without Law: How Neighbors Settle Disputes is a study of, well, its subtitle. The author, Robert Ellickson, is a professor and legal scholar. He comes across as a low-key anarchist, and I've seen him quoted at length on some anarchist websites, and I wouldn't be surprised to learn that he's just a full-blown anarchist. He doesn't identify as one explicitly, at least not here, and he does respect what states bring to the table. He just wishes people would remember that they're not the only game in town. Part of the thesis of the book could be summed up (in my words, not his) as: we credit the government with creating public order, but if you look, it turns out that people create plenty of public order that has basically nothing to do with the legal system. Sometimes there is no relevant law, sometimes the order predates the law, and sometimes the order ignores the law. More on this later.
Part one is an in-depth exploration of Shasta County that I found fascinating, and that I've only given in very brief summary. He goes into much more detail about basically everything.
One oversight is that it's not clear to me how large the population Ellickson studied is. Given that it's a case study for questions of groups maintaining order, I think the size of the group matters a lot. For example, according to wikipedia on Dunbar's number: "Proponents assert that numbers larger than this generally require more restrictive rules, laws, and enforced norms to maintain a stable, cohesive group. It has been proposed to lie between 100 and 250, with a commonly used value of 150."
Does Shasta County support that? I think not, but it's hard to say. Ellickson admittedly doesn't know the population size of the area he studied. (It's a small part of a census division whose population was 6,784 in 1980, so that's an upper bound.) But I feel like he could have been a lot more helpful. Roughly how many ranchers are there, how many ranchette owners, and how many farmers? (I think most of the relevant people are in one of those groups. I'm not sure to what extent we should count families as units. I'm not sure how many people in the area are in none of those groups.) Overall I'd guess we're looking at perhaps 300-1000 people over perhaps 100-300 families, but I'm not confident.
(I tracked down the minutes of the Shasta County Cattlemen's Association, and they had 128 members in June 2011. I think "most ranchers are in the Association but ranchette owners and farmers generally aren't" is probably a decent guess. But that's over twenty years later, so who knows what changed in that time.)
Near the end of part one, Ellickson poses the "what's up with this?" question. Why are the cattlemen so wrong about what range designation means?
His answer is that it's about symbolism. Cattlemen like to think of themselves as being highly regarded in society. But as Shasta County urbanizes, that position is threatened. A closure petition is symbolic of that threat. Open range gives cattlemen more formal rights, even if they don't take advantage of them. It marks them as an important group of people, given deference by the law. So if the range closes, that's an indication to the whole county that cattlemen aren't a priority.
They care about this sort of symbolism - partly because symbols have instrumental value, but also just because people care about symbols inherently. But you can't admit that you care about symbols, because that shows insecurity. So you have to make the battle about something instrumental, and they develop beliefs which allow them to do so. They're fairly successful, too - there haven't been any closures since 1973. (Though I note that Ellickson documents only one attempted closure in that time. It was triggered by a specific rogue cattleman who left the area soon after. It sounds like there may have been other petitions that Ellickson doesn't discuss, but I have no idea how many, what triggered them, or how much support they got. So maybe it's not so much that the cattlemen are successful as that no one else really cares.)
As for how they remain wrong - it simply isn't costing them enough. It costs them some amount, to be sure. It cost one couple $100,000 when a motorist hit three cattle in open range. They didn't have enough liability insurance, and if they'd understood the law, they might have done. But the question is whether ignorant cattlemen will be driven out of work, or even just outcompeted by knowledegable ones. This mistake isn't nearly powerful enough for that. Nor does anyone else have much incentive to educate them about what range designation actually means. So they remain uneducated on the subject.
This all seems plausible enough, though admittedly I'm fairly predisposed to the idea already. For someone who wasn't, I feel like it probably wouldn't be very convincing, and it could stand to have more depth. (Though it's not the focus of the work, so I hope they'd forgive that.) I'd be curious to know more about the couple who didn't have enough insurance - did they increase their insurance afterwards, and do they still think the motorist buys the cow? Did that case encourage anyone else to get more insurance? It seems like the sort of event that could have triggered a wide-scale shift in beliefs.
(Is this just standard stuff covered in works like the Sequences (which I've read, long ago) and Elephant in the Brain (which I haven't)? I'm not sure. I think it's analyzing on a different level than the Fake Beliefs sequence - that seems like more "here's what's going on in the brain of an individual" and this is more "here's what's going on in a society". Also, remember that it long predates those works.)
A counterpoint might be… these cases aren't all that common, and don't usually go to court, and when they do they're usually settled (on the advice of lawyers) instead of ruled. And "lawyers don't understand this specific part of the law" isn't all that implausible. So although the evidence Ellickson presents is overwhelming that the cattlemen are wrong, I'm not sure I can fault the cattlemen too hard for not changing their minds.
Against previous work
Part one was mostly a case study, with some theorizing. It kind of felt like it was building towards the "what's up with this?" question for part two, but instead it gave a brief answer at the end. Part two is a different style and focus: about evenly split between theorizing and several smaller case studies. We're explicitly told this is what's going to happen, but still, it's a little jarring.
Ellickson spends some time criticising previous theories and theorists of social control, which he divides broadly into two camps.
His own background is in the law-and-economics camp, which studies the law and its effects in terms of economic theory. Among other things, this camp notably produced the Coase theorem. But law-and-economics theorists tend to put too much emphasis on the state. Hobbes' Leviathan is a classic example:
Hobbes apparently saw no possibility that some nonlegal system of social control - such as the decentralized enforcement of norms - might bring about at least a modicum of order even under conditions of anarchy. (The term anarchy is used here in its root sense of a lack of government, rather than in its colloquial sense of a state of disorder. Only a legal centralist would equate the two.)
But Coase fell into this trap too:
Throughout his scholarly career, Coase has emphasized the capacity of individuals to work out mutually advantageous arrangements without the aid of a central coordinator. Yet in his famous article "The Problem of Social Cost," Coase fell into a line of analysis that was wholly in the Hobbesian tradition. In analyzing the effect that changes in law might have on human interactions, Coase implicitly assumed that governments have a monopoly on rulemaking functions. … Even in the parts of his article where he took transaction costs into account, Coase failed to note that in some contexts initial rights might arise from norms generated through decentralized social processes, rather than from law.
As have others:
Max Weber and Roscoe Pound both seemingly endorsed the dubious propositions that the state has, and should have, a monopoly on the use of violent force. In fact, as both those scholars recognized elsewhere in their writings, operative rules in human societies often authorize forceful private responses to provocative conduct.
(See what I mean about coming across as a low-key anarchist?)
There's plenty of evidence refuting the extreme version of this camp. We can see that social norms often override law in people's actions. (The Norwegian Housemaid Law of 1948 imposed labor standards that were violated by the employers in almost 90% of households studied, but no lawsuits were brought under it for two years.) People often apply nonlegal sanctions, like gossip and violence. ("Donald Black, who has gathered cross-cultural evidence on violent self-help, has asserted that much of what is ordinarily classified as crime is in fact retaliatory action aimed at achieving social control.") Even specialists often don't know the law in detail as it applies to their speciality. (The "great majority" of California therapists thought the Tarasoff decision imposed stronger duties than it actually did.) And people just don't hire attorneys very often. We saw examples of all of these in Shasta County as well; part one can be seen as a challenge to the law-and-economics camp.
The other camp is law-and-society, emphasizing that the law exists as just one part in the broader scheme of things. These scholars tend to have a more realistic view of how the legal system interacts with other forms of control, but they've been reluctant to develop theory. They often just take norms as given, rather than trying to explain them. The theories they have developed are all flawed, although Ellickson thinks functionalism is on the right track. (This is the idea that norms develop which help a group to survive and prosper.) Ellickson explicitly describes part two as a "gauntlet" thrown towards law-and-society.
(Also, some law-and-society scholars go too far in the other direction, thinking that the legal system is ineffectual. They're just as mistaken. See: Muslim Central Asia after the Russian Revolution; US civil rights laws in the 50s and 60s; range closure in Shasta County; "that the allocation of legal property rights in the intertidal zone affects labor productivity in the oyster industry, that the structure of workers' compensation systems influences the frequency of workplace fatalities, and that the content of medical malpractice law affects how claims are settled." [Footnotes removed.])
The hypothesis
Ellickson has his own theory of norms, which he formed after studying Shasta County. The main thrust of part two is to elaborate and defend it:
Members of a close-knit group develop and maintain norms whose content serves to maximize the aggregate welfare that members obtain in their workaday affairs with one another. … Stated more simply, the hypothesis predicts that members of tight social groups will informally encourage each other to engage in cooperative behavior. [Emphasis original; footnotes removed.]
(He doesn't name this theory, calling it simply "the hypothesis". I admire that restraint, but I kind of wish I had a name to refer to it by.)
Ellickson makes sure to clarify and caveat the hypothesis here, so that we don't interpret it more strongly than he intends. But before looking at his clarifications, I'm going to jump ahead a little, and look at an example he uses of the hypothesis in action.
Consider the Shasta County norm that a livestock owner is strictly responsible for cattle trespass damages. The hypothesis is that this norm is welfare-maximizing. To test that, we have to compare it to alternatives. One alternative would be non-strict liability. Another would be that trespass damages are borne by the victim.
Compared to a negligence standard, strict liability requires less investigation but triggers more sanctions. (Apparently there's a "premise that strict-liability rules and negligence rules are equally effective at inducing cost-justified levels of care", but Ellickson doesn't really explain this.) In Shasta County, the sanctions have basically no transaction costs, since they're just neighbors adjusting mental accounts. So strict liability it is.
To be welfare maximizing, costs should be borne by whoever can avoid them most cheaply. In this case that's the ranchers; I'm not sure I fully buy Ellickson's argument, but I think the conclusion is probably true.
So Ellickson argues that the Shasta County trespass norms support the hypothesis. He also makes a prediction here that things were different in the mid-nineteenth century. "During the early history of the state of California, irrigated pastures and ranchettes were rare, at-large cattle numerous, and motorized vehicles unknown. In addition, a century ago most rural residents were accustomed to handling livestock. Especially prior to the invention of barbed wire in 1874, the fencing of rangelands was rarely cost-justified. In those days an isolated grower of field crops in Shasta County, as one of the few persons at risk from at-large cattle, would have been prima facie the cheaper avoider of livestock damage to crops." And so the farmer would have been responsible for fencing animals out, and borne the costs if he failed to.
Clarifications: "close-knit" and "workaday affairs"
Before we go further, let's look at Ellickson's clarifications. It's important to know what the hypothesis doesn't say.
Ellickson emphasizes that it's descriptive, not normative; it's not a recommendation that norms should be used in preference to other forms of social control. Not all groups are close-knit; welfare isn't the only thing people might want to optimize for; and norms of cooperation within a group often come at the expense of outsiders.
He also emphasizes that a loose reading would give a much stronger version of the hypothesis than he intends. The terms "close-knit", "welfare" and "workaday affairs" are all significant here, and Ellickson explains their meanings in some depth. In order of how much I want to push back against them:
A "close-knit" group is one where "informal power is broadly distributed among group members and the information pertinent to informal control circulates easily among them." This is admittedly vague, but unavoidably so. Rural Shasta County residents are close-knit, and residents of a small remote island are even closer-knit. Patrons of a singles bar at O'Hare Airport are not. Distributed power allows group members to protect their selves and their property, and to personally enforce sanctions against those who wrong them. Information gives people reputations; it allows for punishing people who commit small wrongs against many group members, and for rewarding people who perform those punishments.
Notably, a close-knit group need not be small or exclusive. Someone can be a member of several completely nonoverlapping close-knit groups at once (coworkers, neighborhood, church). And although a small population tends to increase close-knittedness through "quality of gossip, reciprocal power, and ease of enforcement", the size itself has no effect. This is where I think it would be really nice to know how large the relevant population in Shasta County is - as the major case study of the book, it could lend a lot of weight to the idea that large populations can remain close-knit and the hypothesis continues to apply.
"Workaday affairs" means to assume that there's a preexisting set of ground rules, allowing group members to hold and trade personal property. (Which also requires, for example, rules against murder, theft and enslavement.) This is necessary because to calculate welfare, we need some way to measure peoples' values, and we can only do that if people can make voluntary exchanges. The hypothesis doesn't apply to those rules. Seems like a fair restriction.
A little more hackily, it also doesn't apply to "purely distributive" norms, like norms of charity. If you take wealth from one person and give it to another, the transfer process consumes resources and creates none, reducing aggregate welfare. (This is assuming Ellickson's strict definition of welfare, which he's explained by now but I haven't. Sorry.) But clearly norms of charity do exist. There are theories under which they do enhance welfare (through social insurance, or reciprocity). But those might be too simplistic, so Ellickson thinks it prudent to just exclude charity from the hypothesis.
Actually, he goes further than that. He cites Mitch Polinsky (An Introduction to Law and Economics) arguing that for a legal system, the cheapest way to redistribute wealth is (typically) through tax and welfare programs. And so, Polinsky argues, most legal doctrine should be shaped by efficiency concerns, not redistribution. That is, areas like tort and contract law should focus on maximizing aggregate welfare. In a dispute between a rich and a poor person, we shouldn't consider questions like "okay, but the poor person has much more use for the money". In such disputes we should assume the same amount of wealth has equal value whoever's hands it's in, and the point is just to maximize total wealth. Then, if we end up with people having too little wealth, we have a separate welfare system set up to solve that problem.
I can buy that. Ellickson doesn't actually present the argument himself, just says that Polinsky's explained it lucidly, but sure. Stipulated.
Ellickson assumes that the same argument holds for norms as it does for law. Not only that, he assumes that norm-makers subscribe to that argument. That… seems like a stretch.
But granted that assumption, norms would follow a similar pattern: most norms don't try to be redistributive, and if redistribution is necessary, there would be norms specifically for that. For example, the hypothesis predicts "that a poor person would not be excused from a general social obligation to supervise cattle, and that a rich person would not, on account of his wealth, have greater fencing obligations."
That seems entirely reasonable to me, and it's consistent with Shasta County practice. And actually, I don't think we need the strong assumption to get this kind of pattern? It's the kind of thing that plausibly could happen through local dynamics. I would have been happy if Ellickson had just assumed the result, not any particular cause for it. This is a fairly minor criticism though.
(It's a little weird. Normally I expect people try to sneak in strong assumptions that are necessary for their arguments. Ellickson is explicitly flagging a strong assumption that isn't necessary.)
(I'm not sure the words "workaday affairs" was the best way to point at these restrictions. I think I see where he's coming from, but the name doesn't hook into the concept very well for me. But that's minor too.)
Clarification: "Welfare"
This gets its own section because apparently I have a lot to say about it.
The point of "welfare" maximization is to avoid subjectivity problems with utility maximization. I can work to satisfy my own preferences because I know what they are. But I don't have direct access to others' preferences, so I can't measure their utility and I can't work to maximize it.
In Economics, the concepts of Pareto efficiency and Kaldor-Hicks efficiency both work with subjective valuations, people can just decide whether a particular change would make them better off or not. That works fine for people making decisions for themselves or voluntary agreements with others.
But third-party controllers are making rules that bind people who don't consent. They're making tradeoffs for people who don't get to veto them. And they can't read minds, so they don't know people's subjective utilities.
They could try to measure subjective utilities. Market prices are a thing - but at best, they only give the subjective preferences of marginal buyers and sellers. (That is, if I buy a loaf of bread for $1, I might still buy it for $2 and the seller might still sell it for $0.50.) And not everything is or can be bought and sold. We can slightly improve on this with for example the concept of shadow prices but ultimately this just isn't going to work.
(Ellickson doesn't consider just asking people for their preferences. But that obviously doesn't work either because people can lie.)
And so third-party controllers need to act without access to people's subjective preferences, and make rules that don't reference them. Welfare serves as a crude but objective proxy to utility.
We can estimate welfare by using market prices, and looking at voluntary exchanges people have made. (Which is part of the reason for the "workaday affairs" restriction.) When a fence-maintenance credit is used to forgive a looking-after-my-house debit, that tells us something about how much one particular person values those things. This process is "sketchy and inexact", and we just admitted it doesn't give us subjective utilities - but that doesn't mean we can do any better than that.
To be clear, welfare doesn't just count material goods. Anything people might value is included, "such as parenthood, leisure, good health, high social status, and close personal relationships." Ellickson sometimes uses the word "wealth", and while he's not explicit about it, I take that to be the material component of welfare.
What welfare doesn't consider, as I understand it, is personal valuations of things. That is, for any given thing, its value is assumed to be the same for every member of society. "As a matter of personal ethics, you can aspire to do unto others as you would have them do unto you. Because norm-makers don't know your subjective preferences, they can only ask you to do unto others as you would want to have done unto you if you were an ordinary person."
Ellickson doesn't give examples of what this means, so I'll have to try myself. In Shasta County, there's a norm of not getting too upset when someone else's cattle trespass on your land, provided they're not egregious about it. So I think it's safe to suppose that the objective loss in welfare from cattle trespass in Shasta County is low. Suppose, by some quirk of psychology, you found cattle trespass really unusually upsetting. Or maybe you have a particular patch of grass that has sentimental value to you. Cattle trespass would harm your utility a lot, but your welfare only a little - no more than anyone else's - and you'd still be bound by this norm. But if you had an objective reason to dislike cattle trespass more - perhaps because you grow an unusually valuable crop - then your welfare would be harmed more than normal. And so norms might be different. One Shasta County rancher reported that he felt more responsibility than normal to maintain a fence with a neighbor growing alfalfa.
Or consider noisiness and noise sensitivity. Most people get some amount of value from making noise - or maybe more accurately, from certain noisy actions. Talking on the phone, having sex, playing the drums. And most people get some amount of disvalue from hearing other people's noise. In the welfare calculus, there'd be some level of noisemaking that's objectively valued equal to some level of noise exposure. Then (according to hypothesis, in a close-knit group) norms would permit people to be that amount of noisy. If someone was noisier than that, their neighbors would be permitted to informally punish them. If a neighbor tried to punish someone less noisy than that, the neighbor would risk punishment themselves. The acceptable noise level would change depending on the time (objective), but not depending on just "I happen to be really bothered by noise" (subjective). What about "I have young children"? (Or, "some of the inhabitants of that house are young children".) Maybe - that's an objective fact that's likely to be relevant to the welfare calculus. Or "I have a verifiably diagnosed hearing disorder"? Still maybe, but it feels less likely. In part because it's less common, and in part because it's less visible. Both of those seem like they'd make it less… accesible? salient? to whatever process calculates welfare. And if you're unusually noise sensitive and the welfare function doesn't capture that, the cost would fall on you. You could ask people to be quiet (but then you'd probably owe them a favor); or you could offer them something they value more than noise-making; or you could learn to live with it (e.g. by buying noise-cancelling headphones).
So okay. One thing I have to say is, it seems really easy to fall into a self-justifying trap here. Ellickson criticizes functionalism for this, and maybe he doesn't fall into it himself. But did you notice when I did it a couple of paragraphs up? (I noticed it fairly fast, but it wasn't originally deliberate.) I looked at the norms in Shasta County and used those to infer a welfare function. If you do that, of course you find that norms maximize welfare.
To test the hypothesis, we instead need to figure out a welfare function without looking at the norms, and then show that the norms maximize it. In Shasta County, we'd need to figure out how much people disvalue cattle trespass by looking at those parts of their related behaviour that aren't constrained by norms. For example, there seems to be no norm against putting up more fences than they currently do, so they probably disvalue (the marginal cost of cattle tresspass avoided by a length of fence) less than they disvalue (the marginal cost of that length of fence).
How much freedom do we have in this process? If two researchers try it out, will they tell us similar welfare functions? If we look at the set of plausible welfare functions for a society, is the uncertainty correlated between axes? (Can we say "X is valued between $A and $B, Y is valued between $C and $D" or do we have to add "…but if Y is valued near $C, then X is valued near B"?)
And even this kind of assumes there's no feedback from norms to the welfare function. Ellickson admits that possibility, and admits that it leads to indeterminacy, but thinks the risk is slight. (He seems to assume it would only happen if norms change the market price of a good - unlikely when the group in question is much smaller than the market.) I'm not so convinced. Suppose there's a norm of "everyone owns a gun and practices regularly". Then it's probably common for people to own super effective noise-cancelling headphones. And then they don't mind noisy neighbors so much, because they can wear headphones. That's… perhaps not quite changing the welfare function, because people still disvalue noisiness the same, they just have a tool to reduce noisiness? But it still seems important that this norm effectively reduces the cost of that tool. I dunno. (For further reading, Ellickson cites one person making this criticism and another responding to it. Both articles paywalled.)
Separately, I wish Ellickson was clearer about the sorts of things he considers acceptable for a welfare function to consider, and the sorts of calculations he considers acceptable for them to perform. Subjective information is out, sure. But from discussion in the "workaday affairs" section, it seems that "I give you a dollar" is welfare-neutral, and we don't get that result just from eliminating subjective information. We do get it if we make sure the welfare function is linear in all its inputs, but that seems silly. I think we also get it if we also eliminate non-publicly-verifiable information. The welfare function would be linear in dollars, because I can pretend to have more or fewer dollars than I actually do. But it wouldn't need to be linear in the number of children I'm raising, because I can't really hide those. I feel like Ellickson may have been implicitly assuming a restriction along those lines, but I don't think he said so.
Separately again, how closely does welfare correspond to utility? A utility monster couldn't become a welfare monster; I'm not sure if that's a feature or a bug, but it suggests the two can diverge considerably. A few chapters down, Ellickson does some formal game theory where the payoffs are in welfare; is it safe to ignore the possibility of "player gets higher welfare from this quadrant, but still prefers that quadrant"? It seems inevitable that some group members' utilities will get higher weighting in the welfare function than others'; people with invisible disabilities are likely to be fucked over. Ellickson admits that welfare maximization isn't the only thing we care about, but that leaves open the question of how much we should value it at all?
Suppose Quiet Quentin is unusually sensitive to noise, and happy to wear drab clothing. Drab Debbie is unusually sensitive to loud fashion, and happy to be quiet. Each of them knows this. One day Debbie accidentally makes a normal amount of noise, that Quentin isn't (by norm) allowed to punish her for. But wearing a normally-loud shirt doesn't count as punishing her, so he does that. Debbie gets indignant, and makes another normally-loud noise in retaliation, and so on. No one is acting badly according to the welfare function, but it still seems like something's gone wrong here. Is there anything to stop this kind of thing from happening?
It feels weird to me that things like parenthood and personal relationships are a component of the welfare function. Obviously they're a large part of people's subjective utility, but with so much variance that putting an objective value on them seems far too noisy. And what does a system of norms even do with that information?
This one feels very out-there, but for completeness: the reason for using welfare instead of utility is that a norm can't reference people's individual preferences. Not just because they're subjective, but also because there's too many of them; "Alice can make loud noise at any time, but Bob can only make loud noise when Carol isn't home" would be far too complicated for a norm. But when people interact with people they know well, maybe subjectivity isn't a problem; maybe people get a decent handle on others' preferences. And then norms don't need to reference individual preferences, they can just tell people to take others' preferences into account. The norm could be "make loud noise if you value making noise more than others nearby value you not doing that". This feels like it wouldn't actually work at any sort of scale, and I don't fault Ellickson for not discussing it.
Despite all this, I do think there's some "there" there. A decent amount of "there", even. I think Ellickson's use of welfare should be given a long, hard look, but I think it would come out of that ordeal mostly recognizable.
Clarification: Dynamics
There's another clarification that I think is needed. The phrase "develop and maintain" is a claim about dynamics, partial derivatives, conditions at equilibrium. It's not a claim that "all norms always maximize welfare" but that "norms move in the direction of maximizing welfare".
Ellickson never says this explicitly, but I think he'd basically agree. Partly I think that because the alternative is kind of obviously ridiculous - norms don't change immediately when conditions change. But he does also hint at it. For example, he speculates that a group of court cases around whaling arose because whalers were having trouble transitioning from one set of norms to a more utilitarian set (more on this later). Elsewhere, he presents a simple model of a society evolving over time to phase out certain rewards in favor of punishments.
Taken to an extreme, this weakens the hypothesis significantly. If someone points at a set of norms that seems obviously nonutilitarian, we can just say "yeah, well, maybe they haven't finished adapting yet". I don't think Ellickson would go that far. I think he'd say the dynamics are strong enough that he can write a 300-page book about the hypothesis, not explicitly admit that it's a hypothesis about dynamics, and it wouldn't seem all that weird.
Still, I also think this weakens the book significantly. When we admit that it's a hypothesis about dynamics, there's a bunch of questions we can and should ask. Probably the most obvious is "how fast/powerful are these dynamics". But there's also "what makes them faster or slower/more or less powerful" and "to what extent is the process random versus deterministic" and "how large are the second derivatives". (For those last two, consider: will norms sometimes update in such a way as to make things worse, and only on average will tend to make things better? Will norms sometimes start moving in a direction, then move too far in that direction and have to move back?) I'd be interested in "what do the intermediate states look like" and "how much do the individual personalities within the group change things".
I don't even necessarily expect Ellickson to have good answers to these questions. I just think they're important to acknowledge.
(I'd want to dock Ellickson some points here even if it didn't ultimately matter. I think "saying what we mean" is better than "saying things that are silly enough the reader will notice we probably don't mean them and figure out what we do mean instead".)
I think this is my biggest criticism of the book.
Substance
With all these clarifications weakening the hypothesis, does it still have substance?
Yes, Ellickson says. It disagrees with Hobbes and other legal centrists; with "prominent scholars such as Jon Elster who regard many norms as dysfunctional"; with Marxism, which sees norms as serving only a small subset of a group; with people who think norms are influenced by nonutilitarian considerations like justice; and with "the belief, currently ascendant in anthropology and many of the humanities, that norms are highly contingent and, to the extent that they can be rationalized at all, should be seen as mainly serving symbolic functions unrelated to people's perceptions of costs and benefits."
And it's falsifiable. We can identify norms, by looking at patterns of behavior and sanctions, and aspirational statements. And we can measure the variables affecting close-knittedness. ("For example, if three black and three white fire fighters belonging to a racially polarized union were suddenly to be adrift in a well-stocked lifeboat in the middle of the Pacific Ocean, as an objective matter the social environment of the six would have become close-knit and they would be predicted to cooperate.")
But what we can't do is quantify the objective costs and benefits of various possible norm systems. So we fall back to intuitive assessments, looking at alternatives and pointing out problems they'd cause. This is not quite everything I'd hoped for from the word "falsifiable", but it'll do. Ellickson spends the next few chapters doing this sort of thing, at varying levels of abstraction but often with real-world examples. He also makes occasional concrete predictions, admitting that if those fail the hypothesis would be weakened. I'll only look at a few of his analyses.
Lying, and things like it
A common contract norm forbids people from lying about what they're trading. The hypothesis predicts we'd find such norms among any close-knit group of buyers and sellers. I bring this up for the exceptions that Ellickson allows:
Falsehoods threaten to decrease welfare because they are likely to increase others' costs of eventually obtaining accurate information. Honesty is so essential to the smooth operation of a system of communication that all close-knit societies can be expected to endeavor to make their members internalize, and hence self-enforce, norms against lying. Of course a no-fraud norm, like any broadly stated rule, is ambiguous around the edges. Norms may tolerate white lies, practical joking, and the puffing of products. By hypothesis, however, these exceptions would not permit misinformation that would be welfare threatening. The "entertaining deceivers" that anthropologists delight in finding are thus predicted not to be allowed to practice truly costly deceptions. [Footnotes removed; one mentions that "A cross-cultural study of permissible practical joking would provide a good test of the hypothesis."]
It's not clear to me why norms would allow such exceptions, which still increase costs of information and are presumably net-negative. To sketch a possible answer: the edge cases are likely to be where the value of enforcing the norm is lower. I'd roughly expect the social costs of violations to be lower, and the transaction costs of figuring out if there was a violation to be higher. (I feel like I've read a sequence of three essays arguing about one particular case; they wouldn't have been necessary if the case had been a blatant lie.) So, okay, minor violations don't get punished. But if minor violations don't get punished when they happen, then (a) you don't actually have a norm against them; and (b) to the extent that some people avoid those violations anyway, you've set up an asshole filter (that is, you're rewarding vice and punishing virtue).
So plausibly, the ideal situation is for it to be common knowledge that such things are considered fine to do. We might expect this to just push the problem one level up; so that instead of litigating minor deceptions, you're litigating slightly-less-minor deceptions. But these deceptions have a higher social cost, so more value to litigating them, so maybe it's fine.
(Aside, it's not clear to me why the hypothesis specifically expects such norms to be internalized, rather than enforced some other way. Possible answer: you do still need external enforcement of these norms, but that enforcement will be costly. It'll be cheaper if you can mostly expect people to obey them even if they don't expect to get caught, so that relies on self-enforcement. But is that a very general argument that almost all norms should be internalized? Well, maybe almost all norms are internalized. In any case, I don't think that clause was very important.)
Pandering to the SSC audience: dead whales
The second-most-detailed case study in the book is whalers. If a whale is wounded by one ship and killed by another, who keeps it? What if a dead whale under tow is lost in a storm, and found by another ship? The law eventually developed opinions on these questions, but when it did, it enshrined preexisting norms that the whalers themselves had developed.
Ellickson describes a few possible norms that wouldn't be welfare maximizing for them, and which in fact weren't used. For example, a whale might simply belong to whichever ship physically held the carcass; but that would allow one ship to wait for another to weaken a whale, then attach a stronger line and pull it in. Or it might belong to the ship that killed it; but that would often be ambiguous, and ships would have no incentive to harvest dead whales or to injure without killing. Or it might belong to whichever ship first lowered a boat to pursue it, so long as the boat remained in fresh pursuit; but that would encourage them to launch too early, and give claim to a crew who might not be best placed to take advantage of it. Or it might belong to whichever ship first had a reasonable chance of capturing it, so long as it remained in fresh pursuit; but that would be far too ambiguous.
In practice they used three different sets of norms. Two gave full ownership to one party. The "fast-fish/loose-fish" rule said that you owned a whale as long as it was physically connected to your boat or ship. The "first iron" (or "iron holds the whale") rule said that the first whaler to land a harpoon could claim a whale, as long as they remained in fresh pursuit, and as long as whoever found it hadn't started cutting in by then.
Whalers used these norms according to the fishery they hunted from, and each was suited to the whales usually hunted from that fishery. Right whales are weak swimmers, so they don't often escape once you've harpooned them. Fast-fish works well for hunting them. Sperm whales do often break free, and might be hunted by attaching the harpoon to a drogue, a wooden float that would tire the whale and mark its location. The concept of "fresh pursuit" makes first-iron more ambiguous than fast-fish, which isn't ideal, but it allows more effective means of hunting.
(Sperm whales also swim in schools, so ideally you want to kill a bunch of them and then come back for the corpses. If you killed a whale, you could plant a flag in it, which gave you claim for longer than a harpoon. You had to be given reasonable time to come back, and might take ownership even if the taker had started cutting in. Ellickson doesn't say explicitly, but it sounds like American whalers in the Pacific might have had this rule, but not American whalers operating from New England, for unclear reasons.)
The other was a split-ownership rule. A fishery in the Galápagos Islands split ownership 50/50 between whoever attached a drogue and whoever took the carcass. This norm gave whalers an incentive to fetter lots of them and let others harvest them later, but it's not clear how or why that fishery developed different rules than others. On the New England coast, whalers would hunt fast finback whales with bomb-lances; the whales would sink and wash up on shore days later. The killer was entitled to the carcass, less a small fee to whoever found it. This norm was binding even on people unconnected with the whaling industry, and a court upheld that in at least one case. I'm not sure how anyone knew who killed any given whale. Perhaps there just weren't enough whalers around for it to be ambiguous?
(Ellickson notes that the "50/50 split versus small fee" questions is about rules versus standards. Standards let you consider individual cases in more detil, taking into account how much each party contributed to the final outcome, and have lower deadweight losses. But rules have fewer disputes about how they should be applied, and thus lower transaction costs.)
So this is all plausibly welfare-maximizing, but that's not good enough. Ellickson admits that this sort of ex post explanation risks being "too pat". He points out two objections you could raise. First, why did the norms depend on the fishery, and not the fish? (That would have been more complicated, because there are dozens of species of whale. And you had to have your boats and harpoons ready, so you couldn't easily change your technique according to what you encountered.)
More interestingly, what about overfishing? If norms had imposed catch quotas, or protected calves and cows, they might have been able to keep their stock high. Ellickson has two answers. One is that that would have improved global welfare, but not necessarily the welfare of the current close-knit group of whalers, as they couldn't have stopped anyone else from joining the whaling business. This is a reminder that norms may be locally welfare-maximizing but globally harmful.
His other answer is… that that might not be the sort of thing that norms are good at? Which feels like a failure of the hypothesis. Here's the relevant passage:
Establishment of an appropriate quota system for whale fishing requires both a sophisticated scientific understanding of whale breeding and also an international system for monitoring worldwide catches. For a technically difficult and administratively complicated task such as this, a hierarchical organization, such as a formal trade association or a legal system, would likely outperform the diffuse social forces that make norms. Whalers who recognized the risk of overfishing thus could rationally ignore that risk when making norms on the ground that norm-makers could make no cost-justified contribution to its solution. [Footnote removed]
There's some subtlety here, like maybe he's trying to say "norms aren't particularly good at this, so if there's another plausible source of rules, norm-makers would defer to them; but if there wasn't, norm-makers would go ahead and do it themselves". That feels implausible on the face of it though, and while I'm no expert, my understanding is that no other group did step up to prevent overfishing in time.
This section is one place where Ellickson talks about the hypothesis as concerning dynamics. There are only five American court cases on this subject, and four of them involved whales caught between 1852 and 1862 in the Sea of Okhotsk; the other was an 1872 decision about a whale caught in that sea in an unstated year. Americans had been whaling for more than a century, so why did that happen? The whales in that area were bowheads, for which fast-fish may have been more utilitarian than first-iron. Ellickson speculates that "American whalers, accustomed to hunting sperm whales in the Pacific, may have had trouble making this switch."
(He does give an alternate explanation, that by that time the whaling industry was in decline and the community was becoming less close-knit. "The deviant whalers involved in the litigated cases, seeing themselves nearing their last periods of play, may have decided to defect.")
There's something that stuck out to me especially in this section, which I don't think Ellickson ever remarked upon. A lot of norms seem to bend on questions that are unambiguous given the facts but where the facts are unprovable. If I take a whale that you're in fresh pursuit of, I can tell everyone that you'd lost its trail and only found me days later. Who's to know?
Well, in the case of whalers, the answer is "everyone on both of our ships". That's too many people to maintain a lie. But even where it's just one person's word against another's, this seems mostly fine. If someone has a habit of lying, that's likely to build as a reputation even if no one can prove any of the lies.
Remedies
In private (i.e. non-criminal) law, when someone is found to be deviant, the standard remedy is to award damages. That doesn't always work. They might not have the assets to make good; or they might just be willing to pay that price to disrupt someone's world. So the legal system also has the power of injunctions, requiring or forbidding certain future actions. And if someone violates an injunction, the legal system can incarcerate them.
Norms have analagous remedies. Instead of damages, one can simply adjust a mental account. Instead of an injunction, one can offer a more-or-less veiled threat. Instead of incarcerating someone, one can carry out that threat.
Incarceration itself isn't a credible threat ("kidnapping is apt both to trigger a feud and to result in a criminal prosecution"), but other forms of illegal violence are. ("Indeed, according to Donald Black, a good portion of crime is actually undertaken to exercise social control." cite)
Remedial norms require a grievant to apply self-help measures in an escalating sequence. Generally it starts at give the deviant notice of the debt; goes through gossip truthfully about it; and ends with sieze or destroy some of their assets. Gossip can be omitted when it would be obviously pointless, such as against outsiders. This is consistent with the hypothesis, since the less destructive remedies come first in the sequence. It's also consistent with practice in Shasta County, and we see it as well in the lobstermen of Maine when someone sets a trap in someone else's territory. They'll start by attaching a warning to a trap, sometimes sabotaging it without damaging it. If that doesn't work, they destroy the trap. They don't seem to use gossip, perhaps because they can't identify the intruder or aren't close-knit with him.
"Sieze or destroy" - which should you do? Destroying assets is a deadweight loss, so it might seem that siezing them would be better for total welfare. But destruction has advantages too. Mainly, it's more obviously punitive, and so less likely to be seen as aggression and to lead to a feud. The Shasta County practice of driving a cow somewhere inconvenient isn't something you'd do for personal gain. But also, it's easier to calibrate (you can't sieze part of a cow, but you can wound it instead of killing). And it can be done surreptitiously, which is sometimes desired (though open punishment is usually prefered, to maintain public records).
Incentives all the way up
We don't have a good understanding of how norms work to provide order. But the key is "altruistic" norm enforcement by third parties. (Those are Ellickson's scare quotes, not mine.) How do we reconcile that with the assumption of self-interested behavior?
One possibility is internalized norms, where we feel guilty if we fail to act to enforce norms, or self-satisfied if we do act. (I feel like this is stretching the idea of self-interest, but then we can just say we reject that assumption, so whatever.)
Another is that the seemingly altruistic enforcers are themselves motivated by incentives supplied by other third parties. This seems to have an infinite regress. Ellickson gives as example a young man who tackled a pickpocket to retrieve someone's wallet. The woman he helped wrote into the New York Times to publicly thank him, so there's his incentive. But we also need incentives for her to write that letter, and for the editor to publish it, and so on.
(I'm not actually entirely sure where "so on" goes. I guess we also need incentive for people to read letters like that. Though according to Yudkowsky's Law of Ultrafinite Recursion there's no need to go further than the editor.)
This infinite regress seems bad for the chances of informal cooperation. But it might actually help. Ellickson's not entirely detailed about his argument here, so I might be filling in the blanks a bit, but here's what I think he's going for. Suppose there's a virtuous third-party enforcer "at the highest level of social control". That is, someone who acts on every level of the infinite regress. They'll sanction primary behavior as appropriate to enforce norms; but also sanction the people who enforce (or fail to enforce) those norms themselves; and the people who enforce (or fail to enforce) the enforcement of those norms; and so on, if "so on" exists.
Then that enforcer could create "incentives for cooperative activity that cascade down and ultimately produce welfare-maximizing primary behavior." They don't need to do all the enforcement themselves, but by performing enforcement on every level, they encourage others to perform enforcement on every level.
This might work even with just the perception of such an enforcer. God could be this figure, but so could "a critical mass of self-disciplined elders or other good citizens, known to be committed to the cause of cooperation". Art and literature could help too.
Anarchy in academia
Academia seems to have a disproportionate number of legal centrists. So you might think professors would be unusually law-abiding. Not when it comes to photocopying. The law says how they should go about copying materials for use in class: fair-use doctrine is quite restrictive unless they get explicit permission, which can be slow to obtain. Professors decide they don't really like this, and they substitute their own set of norms.
The Association of American Publishers tells us that campus copyright violation is (Ellickson quotes) "widespread, flagrant, and egregious". They seem to be right. Ellickson asked law professors directly, and almost all admit to doing it - though not for major portions of books. The managers of law school copy rooms don't try to enforce the rules, they let the professors police themselves. Several commercial copy centres made multiple copies for him of an article from a professional journal. "I have overheard a staff member of a copy center tell a patron that copyright laws prevented him from photocopying more than 10 percent of a book presented as a hardcopy original; the patron then asked whether he himself could use the copy center's equipment to accomplish that task and was told that he could."
So professors' norms seem to permit illegal repeated copying of articles and minor parts of books. That lets them avoid knowing fair-use doctrine in detail. And since the law would require them to write (and respond to) many requests for consent, it lets them avoid that too.
Professors sense that Congress is unlikely to make welfare-maximizing copyright law. (Publishers can hire better lobbyists than they can.) This lets them frame their norms as principled subversion. I'm not sure if it's particularly relevant though - if copyright law was welfare-maximizing overall, but not for the professors, I think the hypothesis would still predict them to develop their own norms. But thinking back to the stuff on symbolism, maybe "being able to frame your actions as principled subversion" is a component of welfare.
Why will they copy articles, but not large portions of books? Authors of articles don't get paid much for them, and for no charge will mail reprints to colleagues and allow excerpts to be included in compilations. "It appears that most academic authors are so eager for readers to know and cite their work that they usually regard a royalty of zero or even less as perfectly acceptable. For them small-scale copying is not a misappropriation but a service." But book authors do receive royalties, and large-scale copying would diminish those significantly. So according to the hypothesis, this restraint comes from wanting to protect author-professors' royalty incomes, not from caring about publishers' and booksellers' revenues. (Though they might start to care about those, if they thought there might be a shortage of publishers and booksellers. They also might care more about university-affiliated publishers and booksellers.)
(There's a question that comes to mind here, that Ellickson doesn't bring up. Why do professors decline to copy books written by non-academics? I can think of a few answers that all seem plausible: that this is a simpler norm; that it's not necessarily clear who is and isn't an academic; and that it makes it easier to sell the "principled subversion" thing.)
Notably, in the two leading cases around academic copying, the plaintiffs were publishers and the primary defendant was an off-campus copy center. This is consistent with the hypothesis. In these situations, those two parties have the most distant relationship. Publishers have no use for copy centers, and copy centers don't buy many books, so neither of them has informal power over the other. Even more notably, in one of these cases, university-run copy centers weren't included as defendants - that might anger the professors, who do have power over publishers.
Counterexamples?
But Ellickson admits that all of this could be cherry-picking. So he looks at two well-known cases that he expects people to point to as counterexamples. (I hadn't heard of either of them, so I can't rule out that he's cherry-picking here, too. But I don't expect it.)
The first is the Ik of northern Uganda. These are a once-nomadic tribe with a few thousand members. Colin Turnbull found an unsettling pattern of inhumanity among them. Parents were indifferent to the welfare of their children after infancy, and people took delight in others' suffering. In Turnbull's words: "men would watch a child with eager anticipation as it crawled toward the fire, then burst into gay and happy laughter as it plunged a skinny hand into the coals. … Anyone falling down was good for a laugh too, particularly if he was old or weak or blind."
Ellickson replies that the Ik were "literally starving to death" at the time of Turnbull's visit. A few years prior, their traditional hunting ground had been turned into a national park, and now they were forced to survive by farming a drought-plagued area. (Turnbull "briefly presented these facts" but didn't emphasize them.) "Previously cooperative in hunting, the Ik became increasingly inhumane as they starved. Rather than undermining the hypothesis, the tragic story of the Ik thus actually supports the hypothesis' stress on close-knittedness: cooperation among the Ik withered only as their prospects for continuing relationships ebbed." [Footnote removed.]
I note that Wikipedia disputes this account. "[Turnbull] seems to have misrepresented the Ik by describing them as traditionally being hunters and gatherers forced by circumstance to become farmers, when there is ample linguistic and cultural evidence that the Ik were farmers long before they were displaced from their hunting grounds after the formation of Kidepo National Park - the event that Turnbull says forced the Ik to become farmers." To the extent that Ellickson's reply relies on this change in circumstances, it apparently (according to Wikipedia) falls short. But perhaps the important detail isn't that they switched from hunting to farming, but that they switched from "not literally starving to death" to "literally starving to death" (because of a recent drought).
Ellickson also cites (among others) Peter Singer as criticising Turnbull in The Expanding Circle, pp 24-26. Looking it up, Singer points out that, even if we take Turnbull's account at face value, Ik society retains an ethical code.
Turnbull refers to disputes over the theft of berries which reveal that, although stealing takes place, the Ik retain notions of private property and the wrongness of theft. Turnbull mentions the Ik's attachment to the mountains and the reverence with which they speak of Mount Morungole, which seems to be a sacred place for them. He observes that the Ik like to sit together in groups and insist on living together in villages. He describes a code that has to be followed by an Ik husband who intends to beat his wife, a code that gives the wife a chance to leave first. He reports that the obligations of a pact of mutual assistance known as nyot are invariably carried out. He tells us that there is a strict prohibition on Ik killing each other or even drawing blood. The Ik may let each other starve, but they apparently do not think of other Ik as they think of any non-human animals they find - that is, as potential food. A normal well-fed reader will take the prohibition of cannibalism for granted, but under the circumstances in which the Ik were living human flesh would have been a great boost to the diets of stronger Ik; that they refrain from this source of food is an example of the continuing strength of their ethical code despite the crumbling of almost everything that had made their lives worth living.
This seems to support the hypothesis too. I do think there's some tension between these two defenses. Roughly: their circumstances made them the way they were; and anyway, they weren't that way after all. But they don't seem quite contradictory.
The other potential counterexample is the the peasonts in Mentegrano, a southern Italian village, as studied by Edward Banfield.
Banfield found no horrors as graphic as [those of the Ik], but concluded that the Italian peasants he studied were practitioners of what he called "amoral familialism," a moral code that asked its adherents to "maximize the material, short-run advantage of the nuclear family; assume all others will do likewise." According to Banfield, this attitude hindered cooperation among families and helped keep the villagers mired in poverty. [One footnote removed; minor style editing.]
Ellickson has two replies here. Firstly, the evidence is arguably consistent with the hypothesis: some of Banfield's reviewers suggested that, going by Banfield's evidence, the villagers had adapted as well as possible to their environment. Secondly, Banfield's evidence often seems to contradict Banfield's thesis: neighbors have good relationships and reciprocate favors. Banfield apparently discounted that because they did so out of self-interest, but it's still compatible with the hypothesis.
(I don't think these replies are in the same kind of tension.)
For a more general possible counterexample, Ellickson points at primitive tribes believing in magic and engaging in brutal rites. (This is something I did have in my mind while reading, so I'm glad he addressed it.) Some anthropologists are good at finding utilitarian explanations for such things, but Ellickson rejects that answer. Instead, he simply predicts that these practices would become abandoned as the tribe becomes better educated. "A tribe that used to turn to rain dancing during droughts thus is predicted to phase out that ritual after tribe members learn more meteorology. Tribes are predicted to abandon dangerous puberty rites after members obtain better medical information. As tribe members become more familiar with science in general, the status of their magicians and witch doctors should fall. As a more contemporary example, faith in astrology should correlate negatively with knowledge of astronomy. These propositions are potentially falsifiable."
This was my guess as to an answer before I reached this part of the book, which I think says good things about both myself and the book. And I basically agree with his prediction. But I also think it's not entirely satisfactory.
It seems like we need to add a caveat to the hypothesis for this kind of thing, "if people believe that rain dances bring rain, then norms will encourage rain dances". And I kind of want to say that's fair enough, you can't expect norms to be smarter than people. But on the other hand, I think the thesis of The Secret of Our Success and the like is that actually, that's exactly what you can expect norms to be. And it seems like a significant weakening of the hypothesis - do we now only predict norms to optimize in ways that group members understand? Or to optimize not for welfare but for "what group members predict their future welfare will be"? I dunno, and that's a bad sign. But if the hypothesis doesn't lose points for rain dances, it probably shouldn't gain points for manioc. (Though as Ben Hoffman points out, the cost-benefit of manioc processing isn't immediately obvious. Maybe the hypothesis should lose points for both manioc and rain dances.)
If a ritual is cheap to implement, I'd be inclined to give it a pass. There's costs of obtaining information, and that could apply to whatever process develops norms like it does to individuals. Plus, it would only take a small benefit to be welfare-maximizing, and small benefits are probably less obvious than larger ones. (Though if that's what's going on, it's not clear whether we should expect education to phase the rituals out.)
But for vicious and dangerous rituals, this doesn't seem sufficient. Ellickson mentions a tribe where they "cut a finger from the hand of each of a man's close female relatives after he dies"; what medical knowledge are they lacking that makes this seem welfare-maximizing?
I think this is my biggest criticism of the hypothesis.
Another possible counterexample worth considering would be Jonestown, and cults in general. (h/t whoever it was brought this to my attention.) I don't feel like I know enough about these to comment, but I'm going to anyway. I wonder if part of what's going on is that cults effectively don't have the rule of law - they make it costly for you to leave, or to bring in outside enforcers, and so you can't really enforce your property rights or bodily autonomy. If so, it seems like the "workaday" assumption is violated, and the hypothesis isn't in play.
Or, what about dueling traditions? We might again say the "workaday" assumption (that brings rules against murder) is violated, but that seems like a cheat. My vague understanding, at least of pistol dueling as seen in Hamilton, is it was less lethal than we might expect; and fell out of favor when better guns made it more lethal. But neither of these feels enough to satisfy, and we should demand satisfaction. Did the group gain something that was worth the potential loss of life? Alternatively, were such things only ever a transition phase?
Something I haven't touched on is Ellickson's use of formal game theory. To do justice to that section, I split it into its own essay. The tl;dr is that I think he handled it reasonably well, with forgiveable blind spots but not outright mistakes that I noticed. I don't feel like I need to discount the rest of the book (on subjects I know less well) based on his treatment of game theory.
Summing up
Is this a good book? Yes, very much so. I found it fascinating both on the level of details and the level of ideas. Ellickson is fairly readable, and occasionally has a dry turn of phrase that I love. ("A drowning baby has neither the time nor the capacity to contract for a rescue.") And I don't know if this came across in my review, but he's an unusually careful thinker. He owns up to weaknesses. He rejects bad arguments in favor of his position. He'll make a claim and then offer citations of people disagreeing. He makes predictions and admits that if they fail the hypothesis will be weakened. I think he made some mistakes, and I think his argument could have been clearer in places, but overall I'm impressed with his ability to think.
Is the hypothesis true? I… don't think so, but if we add one more caveat, then maybe.
The hypothesis says that norms maximize welfare. Note that although Ellickson calls the welfare function "objective", I think a better word might be "intersubjective". The welfare function is just, like, some amorphous structure that factors out when you look at the minds of group members. Except we can't look at their minds, we have to look at behaviour. The same is true of norms themselves: to figure out what the norms are in a society we ultimately just have to look at how people in that society behave.
And so if we're to evaluate the hypothesis properly, I think we need to: look at certain types of behaviour, and infer something that's reasonable to call "norms"; and then look at non-normative behavior - the behaviour that the inferred system of norms doesn't dictate - and infer something that's reasonable to call a "welfare function". And then the hypothesis is that the set of norms will maximize the welfare function. ("Maximize over what?" I almost forgot to ask. I think, maximize over possible systems of norms that might have been inferred from plausible observed behaviour?)
Put like that it sounds kind of impossible. I suspect it's… not too hard to do an okay job? Like I'd guess that if we tried to do this, we'd be able to find things that we'd call "norms" and "a welfare function" that mostly fit and are only a little bit circular; and we wouldn't have an overabundance of choice around where we draw the lines; and we could test the hypothesis on them and the hypothesis would mostly come out looking okay.
But to the extent that we can only do "okay" - to the extent that doing this right is just fundamentally hard - I suspect we'll find that the hypothesis also fails.
There are problems which are known to be fundamentally hard in important ways, and we can't program a computer to reliably solve them. Sometimes people say that slime molds have solved them and this means something about the ineffable power of nature. But they're wrong. The slime molds haven't solved anything we can't program a computer to solve, because we can program a computer to emulate the slime molds. What happens is that the slime molds have found a pretty decent approach to solving the problem, that usually works under conditions the slime molds usually encounter. But the slime molds will get the wrong answer too, if the specific instance of the problem is pathological in certain ways.
In this analogy, human behavior is a slime mold. It changes according to rules evaluated on local conditions. (Ellickson sometimes talks about "norm-makers" as though they're agents, but that feels like anthropomorphising. I expect only a minority of norms will have come about through some agentic process.) It might be that, in doing so, it often manages to find pretty good global solutions to hard problems, and this will look like norms maximizing welfare. But when things are set up right, there'd be another, better solution.
(I'm not sure I've got this quite right, but I don't think Ellickson has, either.)
So I want to add a caveat acknowledging that sort of thing. I don't know how to put it succinctly. I suspect that simply changing "maximize" in the hypothesis to "locally maximize" weakens it too far, but I dunno.
With this additional caveat, is the hypothesis true? I still wouldn't confidently say "yes", for a few reasons. My main inside-view objections are the ritual stuff and duelling, but there's also the outside-view "this is a complicated domain that I don't know well". (I only thought of duelling in a late draft of this review; how many similar things are there that I still haven't thought of?) But it does feel to me like a good rule of thumb, at least, and I wouldn't be surprised if it's stronger than that.
Further questions
I want to finish up with some further questions.
-
The world seems to be getting more atomic, with less social force being applied to people. Does that result in more legal force? Ellickson gives a brief answer: "In [Donald Black's] view, the state has recently risen in importance as lawmakers have striven to fill the void created by the decline of the family, clan, and village." (Also: "increasing urbanization, the spread of liability insurance, and the advent of the welfare state". But Black speculates it'll decline in future because of increasing equality. And although the number of lawyers in the US has increased, litigation between individuals other than divorce remains "surprisingly rare".)
-
Can I apply this to my previous thoughts on the responsibility of open source maintainers? When I try, two things come to mind. First, maintainers know more about the quality of their code than users. Thus, if we require maintainers to put reputation on the line when "selling" their code, we (partially) transfer costs of bad code to the people who best know those costs and are best able to control them. So that's a way to frame the issue that I don't remember having in mind when I wrote the post, that points in the same directions I was already looking. Cool. Second, I feel like in that post I probably neglected to think about transaction costs of figuring out whether someone was neglecting their responsibility? Which seems like an important oversight.
-
To test the hypothesis, I'd be tempted to look at more traditions and see whether those are (at least plausibly) welfare-maximizing. But a caveat: are traditions enforced through norms? I'd guess mostly yes, but some may not be enforced, and some may be enforced through law. In those cases the hypothesis doesn't concern itself with them.
-
Making predictions based on the hypothesis seems difficult. Saying that one set of norms will increase welfare relative to another set might be doable, but how can you be confident you've identified the best possible set? Ellickson does make predictions, and I don't feel like he's stretching too far - though I can't rule it out. But I'm not sure I'd be able to make the same predictions independently. How can we develop and test this skill?
-
Sometimes a close-knit group will fracture. What sort of things cause that? What does it look like when it happens? What happens to the norms it was maintaining?
-
What are some follow-up things to read? Ellickson approvingly cites The Behavior of Law a bunch. If we want skepticism, he cites Social Norms and Economic Theory a few times. At some point I ran across Norms in a Wired World which looks interesting and cites Ellickson, but that's about all I know of it.
-
How does this apply to the internet? I'd note a few things. Pseudonymity (or especially anonymity) and transience will reduce close-knittedness, as you only have limited power over someone who can just abandon their identity. To the extent that people do have power, it may not be broadly distributed; on Twitter for example, I'd guess your power is roughly a function of how many followers you have, which is wildly unequal. On the other hand, public-by-default interactions increase close-knittedness. I do think that e.g. LessWrong plausibly counts as close-knit. The default sanction on reddit is voting, and it seems kind of not-great that the default sanction is so low-bandwidth. For an added kick or when it's not clear what the voting is for, someone can write a comment ("this so much"; "downvoted for…"). That comment will have more weight if it gets upvoted itself, and/or comes from a respected user, and/or gets the moderator flag attached to it. Reddit also has gilding as essentially a super-upvote. For sanctioning remedial behavior, people can comment on it ("thanks for the gold", "why is this getting downvoted?") and vote on those comments. But some places also have meta-moderation as an explicit mechanism.
-
How much information is available about historical norms and the social conditions they arose in? Enough to test the hypothesis?
-
There's a repeated assumption that if someone has extraordinary needs then it's welfare maximizing for the cost to fall on them instead of other people. I'm not sure how far Ellickson would endorse that; my sense is that he thinks it's a pretty good rule of thumb, but I'm not sure he ever investigates an instance of it in enough detail to tell whether it's false. It would seem to antipredict norms of disability accomodation, possibly including curb cuts. (Possibly not, because those turn out to benefit lots of people. But then, curb cuts are enforced by law, not norm.) This might be a good place to look for failures of the hypothesis, but it's also highly politicized which might make it hard to get good data.
-
Ellickson sometimes suggests that poor people will be more litigous because they have their legal fees paid. We should be able to check that. If it's wrong, that doesn't necessarily mean the hypothesis is wrong; there are other factors to consider, like whether poor people have time and knowledge to go to court. But it would be a point in favor of something like "the hypothesis is underspecified relative to the world", such that trying to use it to make predictions is unlikely to work.
-
Is Congress close-knit? Has that changed recently? Is it a good thing for it to be close-knit? (Remember, norms maximizing the welfare of congresspeople don't necessarily maximize the welfare of citizens.)
-
Does this work at a level above people? Can we (and if so, when can we) apply it to organizations like companies, charities, and governments?
-
Suppose the book's analysis is broadly true. Generally speaking, can we use this knowledge for good?
Posted on 10 July 2021
|
Comments
I listen to podcasts while doing chores or at the gym, and often feel like I'm learning something but then can't really remember anything afterwards. So for the past ~month I've been doing an experiment where I write brief summaries of them afterwards, usually same-day but sometimes a bit later. Generally I avoid all forms of fact checking, both "what did the episode say" and "what is actually true", though I don't stop myself if I feel like doing it.
I've been posting them to my shortform on LessWrong. Mostly in reply to a single comment for tidiness, but two of them I accidentally posted to the top of the thread and one as a reply to another. Initially that was just because I wanted to be able to write them from both my work and personal laptops. (This blog is published through git. I don't have the repo on my work laptop, and probably shouldn't do.) But I kind of like it. A downside is it's slightly less convenient to include episode numbers or air dates or even titles unless I remember them. So I might be less consistent about that, though it feels good to have a fairly straightforward way to look up the episode given my summary.
I've skipped all the fiction podcasts I listen to, because that's not why I listen to fiction. Also most interviews, those seem generally hard to summarize, though it would probably be reasonable to extract a few individual points. And one Planet Money episode seemed like it would be irresponsible to summarize carelessly, and I didn't feel like trying to be careful about it. But I've summarized every episode of 99% Invisible and History of English, and all but that one episode of Planet Money, that I've listened to in this time. Also one episode of Rationally Speaking and one of Corecursive.
I'm not really sure what this experiment was trying to test. I was curious, so I did it. Some things I've maybe vaguely learned: first, I think I can generally do a decent summary. I frequently get distracted for a few seconds at a time, but there's a difference between that and being actually distracted, and I think it shows. (I listened to 99% Invisible, "Tanz Tanz Revolution", while looking at parking restrictions in my area and anticipating my evening plans. There's significant parts of that episode that just rolled right past me.) I don't think you could reliably pick out the episodes I didn't do same-day, I mostly don't even remember myself. (Hot Cheetos was several days later, but I did go over it a bit in my head in between, which I wouldn't have done if not for this project.)
Second, I seem to retain less of History of English than other podcasts. That feels like it matches my intuition. I expect Causality, too, but that only recently released a new episode and I haven't listened to it yet.
Third, this causes a marginal shift from podcasts towards music for me. I predicted this and I'm okay with it, I feel like I don't listen to music enough relative to how much I enjoy it.
If I wanted to make it more of an experiment, I could randomly select some episodes to write up quickly, some to write up the next day, the next week, next month. Not sure how much I feel like this, but maybe. Another thing would be quizzing me on the episodes I did and didn't write up, without rereading. And I'm curious whether I'll ever actually want to refer to these, and if so whether I can predict which ones I will.
I haven't been tracking my time closely, but I think they mostly take me 20-30 minutes to write? I listen between 1.5x and 2.1x speed depending on the podcast, so that's considerably longer than they usually take to listen to.
Dunno what I'll do in future. Maybe write up some summaries, of episodes I found particularly interesting?
I'm including here three that I particularly liked, but if you feel like reading the rest see the LW thread.
Planet Money (14 May 2021): Blood Money
America lets you sell blood plasma for money. The centers will call it a donation, but you get money for it, so. You can come in a couple of times a week and especially for low income people it can be a significant addition to their income. There are referral bonuses, and you get paid more if you come in more often. (Seems weird?) These centers are mostly located in low-income areas.
There's a history here involving Nicaragua. Under a dictator there was a center doing this, and a journalist was writing about concerns, and eventually the dictator had the journalist killed. Riots in the aftermath left the center burned down and eventually the dictator got deposed. At some point the WHO wrote up an agreement or something not to allow blood plasma to be sold. Almost everyone's signed, but not the USA. Now almost everyone gets their blood plasma from the USA. Four exceptions, who allow it to be sold and are self-sufficient: Germany, Austria, Czech Republic, Hungary.
(Farmer's Dilemma!)
We speak to a Canadian healthcare person about why Canada doesn't allow it. Three concerns. He's not too worried about incentives for people to sell bad blood, apparently we can sanitize it, even of HIV. He's also not too worried about health impacts on sellers; they get a checkup every four months to make sure they're still good, and there's some anecdotal evidence that maybe it should be more frequent but basically it seems fine. He seemed more concerned about "if people can sell plasma, will they do other things like regular blood donation for free?" I don't remember the commentary on that. I think he said that if the USA didn't allow selling they'd probably have to in Canada, but as long as they do it's unlikely to change.
We also speak to a Brazilian doctor saying that plasma and the things it's used for are essential, there are people who will die without it, get over yourselves.
Concerns that if either demand raises (finding new uses: there are studies showing promise in Alzheimers) or supply drops, there might not be enough. In fact supply has dropped during Covid: possible reasons include "sellers need the money less thanks to stimulus"; "if your kids are at home all the time you might be too busy"; "a lot of the sellers near the border are Mexicans who can't come over any more".
99% Invisible #434 (9 Mar 2021): Artistic License
This is the most American story. (I actually wrote it up before starting this experiment.)
After states start requiring license plates, Idaho realizes they can be used for advertising, and start boasting about Idaho potatoes on their plates. North Idahoans grumble because that’s more of a Southeast Idaho thing. Tourists start stealing plates as souvenirs, causing people to be very confused when they’re pulled over because who checks whether they still have a license plate.
Anyway, New Hampshire’s state motto is Live Free or Die, I don’t know if that’s just a generic America thing or a specifically fuck-communists America thing. But a super fuck-communists guy gets them to put the motto on the license plate, presumably for fuck-communists reasons but I dunno if that was explicit or just subtext.
And then a Jehova’s Witness is like, no, I don’t want to, God gave me life and I’m not gonna give that up for freedom. So he starts covering up that bit with tape. And he gets arrested and the fuck-communists guy is now governor and not inclined to give an inch, so it goes to the Supreme Court who split 6-3 but the pro-freedom side wins, the government is not allowed to compel you to express your love of freedom.
Later: Texas allows specialty plates, some group designs a plate to support a cause and then you pay a little extra for it, some going to the group and some to the state. Most of these designs are just rubber stamped. But this is Texas, so the Sons of Confederate Veterans want a license plate supporting their cause, and they want the Confederate flag on it. The state says no, they sue the state, and the Supreme Court sides with the state 5-4.
Corecursive (2 May 2021): Etherium Rescue
"Daryl" was an ETH user who fat-fingered a transaction. Went online for help, guest said sorry, nothing anyone can do. Then later guest went o shit maybe there is.
Daryl was playing with uniswap, a smart contract letting people provide liquidity for exchanging crypto, e.g. ETH for USDC. Normally when providing liquidity you'd do two things in one transaction, with something like a try/catch letting you do them atomically. I guess Daryl had only done one of them? Anyway, his money was just sitting there, and as soon as anyone tried to take their liquidity from uniswap they'd get Daryl's money as well.
Guest realized this and went to check, and the money was still there. But! He also remembered stories of generalized ETH frontrunners. These will examine the pending transactions, see if there's something in there they can use to make money, and if so, submit their own transaction with a higher fee so it gets executed first. Guest worried that one of these would show up if he tried to recover the money. He asked on a group chat if others would also be worried, some of them were, and they got together to try to figure something out.
Ultimately they'd need to do some kind of obfuscation so that a bot wouldn't try the thing they were doing. They settled on two separate transactions in one block, where the second one wouldn't do anything unless the first had already happened, hoping bots would only try them separately. But there's stuff set up to protect you from making transactions that don't do anything, and it was stopping them from making the second.
Guest was tired and stressed and the money might disappear at any minute, so eventually Guest said YOLO we'll do them in two different blocks and hope. The second transaction got front-ran and they lost the money. On the plus side his worries were vindicated.
Guest and Adam (host) discuss Meditations on Moloch. The thing they take away from it is that you need regulation/Leviathan. Guest says for Hobbes the Leviathan was hereditary monarchy, recently we've been trying democracy and that seems better overall, but he's optimistic that smart contracts will be another solution.
Posted on 27 May 2021
|
Comments
Sometimes I'm at my command prompt and I want to draw a graph.
Problem: I don't know gnuplot. Also, there's a couple things about it that bug me, and make me not enthusiastic about learning it.
One is that it seems not really designed for that purpose. It implements a whole language, and the way to use it for one-off commands is just to write a short script and put it in quotes.
The other is its whole paradigm. At some point in the distant past I discovered ggplot2, and since then I've been basically convinced that the "grammar of graphics" paradigm is the One True Way to do graphs, and everything else seems substandard. No offense, gnuplot, it's just… you're trying to be a graphing library, and I want you to be a graphing library that also adheres to my abstract philosophical notions of what a graphing library should be.
If you're not familiar with the grammar of graphics, I'd summarize it as: you build up a graph out of individual components. If you want a scatter plot, you use the "draw points" component. If you want a line graph, you use the "draw line segments" component. If you want a line graph with the points emphasized, you use both of those components. Want to add a bar chart on top of that too? Easy, just add the "draw bars" component. Want a smoothed curve with confidence intervals? There's a "smooth this data" component, and some clever (but customizable) system that feeds the output of that into the "draw a line graph" and "draw a ribbon" components. Here's a gallery of things it can do
So, rather than adapt myself to the world, I've tried to adapt the world to myself.
There's a python implementation of the paradigm, called plotnine. (It has its own gallery.) And now I've written a command-line interface to plotnine.
It's not as powerful as it plausibly could be. But it's pretty powerful, and if I stop developing now I might find it fully satisfies my needs in future. For example, I took a dataset of covid cases-per-capita timeseries for multiple countries. Then both of these graphs came from the same input file, only manipulated by grep to restrict to twelve countries:
(The second one isn't a type of graph that needs to be implemented specifically. It's just a combination of the components "draw points", "draw line segments" and "draw text".)
Now admittedly, I had to use a pretty awful hack to get that second one to work, and it wouldn't shock me if that hack stops working in future. On the other hand, I deliberately tried to see what I could do without manipulating the data itself. If I wasn't doing that, I would have used a tool that I love named q, which lets you run sql commands on csv files, and then there'd be no need for the awful hack.
Anyway. If you're interested, you can check it out on github. There's documentation there, and examples, including the awful hack I had to use in the above graph. To set expectations: I don't anticipate doing more work on this unprompted, in the near future. But if people are interested enough to engage, requesting features or contributing patches or whatever, I do anticipate engaging back. I don't want to take on significant responsibility, and if this ever became a large active project I'd probably want to hand it over to someone else, but I don't really see that happening.
Posted on 30 March 2021
|
Comments
A while back I wrote about Haskenthetical, a language that I'm implementing for fun. I'm still working on it, at least from time to time.
The thing I'm pleased to have implemented recently is user-defined macros. This makes it potentially a lot more ergonomic.
(You still can't do anything with it, really. It has no I/O except for printing a single value at the end, and that's in a constrained format. It's beyond the reach even of sysfuck. But, like. If you could do things with it, user-defined macros would make it nicer to do those things.)
These aren't hygienic macros, partly because when I used Racket a little at my old job I never really got my head around those, but also because they would have been more work. I'm more inclined to go for Clojure's approach of namespace qualifying, but since I don't have any kind of namespaces yet it seems premature to think of that.
Quasiquote
The biggest test of Haskenthetical yet has been using these macros to implement ¶ quoting (quote, like a standard lisp ') and quasiquoting (qq, like `, using ↑ and ↑↑ for splicing). Quasiquoting in particular was one of the hardest pieces of code I think I've ever written, and it's only 100 lines in the end. Some of the things that made it difficult:
-
Haskenthetical is deficient. Pattern-matching causes deep nesting and the chance of forgetting a case, while type eliminators are hard to read and flow poorly. (It's deficient in many many ways, but those are the ones that seem particularly relevant here.)
-
More importantly, the current implementation of Haskenthetical is deficient. The error messages are completely unhelpful, telling you that two types didn't unify but not where they occured. Both the debugging output and the output from the program itself are hard to read. I also uncovered one straight-up bug in the process, which was easy to fix when I tracked it down but hard to track down because the error messages are completely unhelpful.
-
Also, I'm deficient as a thinker. I have a brain architecture that can't easily distinguish between the object and the meta levels, or the meta and the meta-meta levels. Wtf, who designed this piece of shit?
-
The problem itself is well-targeted to hit those last two deficiencies. The quasiquote function simply converts syntax trees to syntax trees, but some of the trees in question represent Haskenthetical expressions of certain types, and some of the transformations need to preserve or manipulate those types. The type checker could tell me "you're passing a list of trees somewhere you should be passing a single tree", but since everything is either a tree or a list of trees that doesn't narrow things down much. And it couldn't tell me "you're trying to convert this list-of-trees to a tree-evaluating-to-a-list but you've actually created a tree-evaluating-to-a-type-error".
Eventually I simplified the problem by first parsing a syntax tree into a new datatype, and then converting that new datatype into another syntax tree, giving slightly more type information. That also made it easier to perform some simplifications in the parsing step, which made the output simpler and easier to check. Ultimately this brought it to a level that my brain could handle.
The result is that you can implement macros by describing the shape of the code they could generate, rather than implementing something that evaluates to that shape. Here are two ways to write an if-elsif-else macro (technically only the "else" is necessary):
(defmacro if
(λ ts
(if~ ts (Cons $else Nil)
else
(if~ ts (Cons $cond (Cons $then $rest))
(STTree (» Cons (STBare "if~")
cond
(STBare "True")
then
(STTree (Cons (STBare "if") rest))
Nil))
(error! "`if` must have an odd number of args")))))
(defmacro if-qq
(λ ts
(if~ ts (Cons $else Nil)
else
(if~ ts (Cons $cond (Cons $then $rest))
(qq (if~ (↑ cond) True (↑ then) (if-qq (↑↑ rest))))
(error! "`if` must have an odd number of args")))))
In the first, we manually construct a SyntaxTree with the STTree constructor (which represents syntax like (...)), passing it an argument of type List SyntaxTree. In the second, we construct the same SyntaxTree using quasiquoting, with splices ↑ and ↑↑ to indicate where the input parameters go. ↑ expects its parameter to be a SyntaxTree, which gets interpolated directly, while ↑↑ expects its parameter to be a List SyntaxTree, each element of which gets interpolated. So (if-qq a b c d e) macroexpands once to (if~ a True b (if-qq c d e)), and ultimately to (if~ a True b (if~ c True d e)).
There's another macro I use in the first definition: » and « can be used to "make functions variadic" by threading them in between other parameters like a fold. We have
(» f a b c d) === (f a (f b (f c d)))
(« f a b c d) === (f (f (f a b) c) d)
These are built-in, but they don't need to be. It's partly a matter of convenience, and partly because I implemented them to test macroexpansion before I implemented user-defined macros.
Implementation
There's a circularity problem when defining macros. Sometimes you'll want to do so using functions you've previously defined. And sometimes you'll want to use a macro to help define a function. Allowing either one of these seems easy enough, but how do you do both?
I don't know how lisps handle this problem. I don't remember it ever tripping me up when I used them (I have some experience with Common Lisp, Clojure and Racket), but that was years ago and maybe I just didn't stress test them properly.
Haskell solves it with modules. You can't call a macro in the same module you define it. In Haskell's case that also means not in the same file you define it. That's fine for Haskell I guess, but I wouldn't want it for Haskenthetical.
But getting rid of one-module-per-file, this seemed like a reasonable solution. So I added a new top-level form, (declarations ...). With this, the order of events is:
-
Parse the input file into a list of SyntaxTree (trees whose leaves are barewords, floats and strings). Separate trees into those of the form (declarations ...) and all others.
-
For each (declarations ...) block,
-
Parse its children into statements ((def ...), (type ...), (defmacro ...)) and expressions (underneath def and defmacro). In this step, we have a list of macros available in the environment, and recognize when those are being called, declining to parse the arguments to macros.
-
Recursively macroexpand the result, evaluating macros (which can be builtins written in Haskell or Haskenthetical closures) on their arguments. Since macros convert SyntaxTrees directly to SyntaxTrees, we have to parse the result of each expansion.
-
Add all the type declarations ((type ...)) to the environment, along with their constructors and eliminators. We have to do this simultaneously, because types can be mutually recursive.
-
Type check all the value definitions. This has to be simultaneous too, for the same reason. If type checking passes, add them to the environment, which doesn't strictly need to be simultaneous but is forced to be by my implementation. (Every defined value is a thunk storing a copy of the environment at the time it was defined. These environments do need to be mutually recursive.)
-
Type check the macro declarations, and add them to the environment. The type of a macro is -> (List SyntaxTree) SyntaxTree, I think it's pretty okay for macros to be impure but in future they'll need to be augmented with some way for macros to consult the environment. We can do these one at a time, because macros declared in the same block can't reference each other directly. (They can generate references to each other.)
-
Treat the remaining top-level trees as another (declarations ...) block, and go through the same process. But this block is required to also contain a single top-level expression, after macroexpansion.
-
Type check that expression. If type checking passes, evaluate it in the environment we've been building up.
I don't know if this approach is standard. It seems to work. It doesn't allow macros to expand to declarations blocks, which is a shame. In future, if I implement importing from other files, I might figure out how to allow macros defined in other files to expand to those blocks. On the other hand, once I have IO it would be interesting to see if I can implement importing from other files purely in Haskenthetical, and use declarations blocks as the only built-in form of module. That would be great and terrible.
Other things
I've added comments now. # is a comment to end of line, but it has to be surrounded by whitespace, because I don't want to eliminate the possibility of using that character in combination with other things. #! works the same, to allow shebang lines. I don't yet have multiline comments, or single-form comments.
I also have an emacs major mode, which parses comments badly because emacs' easy-mode syntax highlighting only supports fairly specific kinds of syntax. But it's better than nothing.
I discovered two bugs writing the previous post. The type checker was ignoring type annotations on λ parameters. I've fixed that. It also wasn't giving an error if a type annotation in a pattern match was more general than the type it matched. I've only partly fixed that. I think to fix it more thoroughly I'd need to implement constraints and constraint solving. I might also decide to eliminate that feature - GHC is going in that direction.
What's next?
(Assuming I continue at all, that is. This is fun, but it's not the only fun thing.)
I dunno. The test suite is looking a bit embarrassing, I've only added a handful of new tests since I first wrote about this project. At first I wanted them to be nicely grouped, tests about type checking and type declaration and evaluation, but there's no clear division and I shouldn't try for it. Instead I think I'll just have one big file with lots of examples and some metadata.
One thing is that macros can't currently be used in types or patterns. So you can write (list a b c) instead of (Cons a (Cons b (Cons c Nil))) when constructing a list, but not when destructing it. And you can't write a three-argument function type as (» -> a b c d). This should be some fairly low-hanging fruit.
Writing the quasiquoter made me want better error messages. That's definitely not low-hanging fruit though. Especially with macros in play - how do you give the location of an error in the file when any given piece of syntax might not have been in the original file? There are options here but also, annotating everything with a source location sounds boring even if I didn't have to worry about macros.
Another possibility is to look at the type checker only. Write You a Haskell implements it in two different ways in the same chapter. I followed the second approach, section "constraint generation", because Diehl says it "becomes easier to manage as our type system gets more complex and we start building out the language". But it means that by the time I get a type error, I've lost all context. The types String and Float should unify but don't, great, but I have no idea why I'd expect either of those. And I'm not convinced it accomplishes its goal - the point is to separate constraint solving from traversing the tree, but you still need to solve constraints when you generalize a variable during traversal (the implementation on the page is buggy).
I think the first approach in WYAH is also used by Typing Haskell in Haskell, where you solve constraints as you traverse the program. Then the context is still there when you encounter a type error, which might make it easier to report a helpful error message.
Half the macros I've written so far (», «, list) could simply be functions, except Hindley-Milner doesn't have variadic functions. Can it be expanded to have them? The paper practical variable-arity polymorphism looks interesting on this question, though I haven't looked closely or thought deeply. I'd be going even further out of my comfort zone, but that's not a bad thing.
I've been thinking about nomenclature a bit. Right now the Either type is called +, which might make sense if the , type was called * but it's called ,. List and Maybe aren't built-in, but when I've been defining them I've been calling them List and Maybe with constructors Nil Cons Nothing Just. I'm thinking I might go with regex-inspired names,
- The unit type becomes
ε, with constructor also ε.
+ $a $b becames || $a $b. Constructors _| $a and |_ $b, perhaps. (But which way around? I have no intuition for that.)Maybe $a becomes ?? $a. Constructors ι $a and ?ε. (ι is the inclusion map -> $a (?? $a). But lots of types might want one of those, so maybe it should be ?ι, with ι for the only constructor of the type ι $a. Will Haskenthetical find that type useful like Haskell does?)List $a becomes ** $a. Constructors :: $a (** $a) and *ε, but I'm not sold on ::.
This seems pretty terrible, how do you pronounce any of that? But it also seems kind of fun.
Posted on 14 March 2021
|
Comments
I have three purposes in this post. The first is to review the formal game theory found in Robert Ellickson's Order Without Law. It's not a large part of the book, but it's the part that I'm most qualified to judge. Not that I'm a formal game theorist myself, but I'm closer to being one of them than to being any kind of social scientist, historian or lawyer. If his formal game theory is nonsense, that would suggest that I ought to discount his writing on other fields, too. (Perhaps not discount it completely, especially because formal game theory is outside his main area of study. Then again, lots of the book is outside his main area of study.)
Spoiler alert: I think he holds up reasonably well. I want to ding him a few points, but nothing too serious, and he possibly even contributes a minor original result.
My second purpose, which is valuable for the first but also valuable of itself, is to try to extend it further than Ellickson did. I don't succeed at that.
My third is simply to be able to cut it from my in-progress review of the rest of the book.
Ellickson discusses two games. One is the classic Prisoner's Dilemma, in which you either Cooperate (for personal cost but social benefit) or Defect (for personal benefit but social cost). The other he calls Specialized Labor, in which two people must choose whether to Work on some common project or Shirk their share of it. It differs from the Prisoner's Dilemma in two ways. First, it's asymmetrical; one player is a less effective worker than the other, and gets less payoff from Working while the other Shirks than does the other player. The other is that in this game, the socially optimal outcome is Work/Shirk, not Work/Work.
(Many authors consider that the second change isn't really a change, and that a Prisoner's Dilemma can perfectly well have Cooperate/Defect be socially optimal. So they'd say Specialized Labor is simply an asymmetrical version of the Prisoner's Dilemma. In my taxonomy I define the Prisoner's Dilemma more narrowly than that; see also this comment. Ellickson uses the same narrow definition as me. I'd instead say Specialized Labor is an asymmetrical version of Too Many Cooks.)
Note that payoffs aren't measured in utility. They're measured in something Ellickson calls "welfare". He doesn't really explore the formal consequences of this. But what it gives us is that, since welfare is supposed to be objective, we can sum different people's welfare; when I used the phrases "social cost" and "socially optimal" in the previous paragraphs, talking about the sum of both players' results, that was a meaningful thing to do. I'm not sure exactly what it costs us, except that I don't expect results about mixed strategies to hold. (Someone won't necessarily prefer "50% chance of 3 welfare" to "certain chance of 1 welfare". I wasn't planning to consider mixed games anyway.) We can still assume that people prefer higher amounts of welfare to lower amounts of it.
I'm going to pretend that Cooperate and Defect are also called Work and Shirk, so that I don't have to use both names when talking about both games.
In normal-form, these games look like this:
| Prisoner's Dilemma |
|
|
Player 2 |
|
|
Work |
Shirk |
| Player 1 |
Work |
$ ww_* $,
$ ww_* $
|
$ ws_* $,
$ sw_* $
|
| Shirk |
$ sw_* $,
$ ws_* $
|
$ ss_* $,
$ ss_* $
|
| $ sw_* > ww_* > ss_* > ws_* $, and $ 2ww_* > sw_* + ws_* $ |
Specialized Labor
|
|
|
Player 2 |
|
|
Work |
Shirk |
| Player 1 |
Work |
$ ww_* $,
$ ww_* $
|
$ ws_1 $,
$ sw_* $
|
| Shirk |
$ sw_* $,
$ ws_2 $
|
$ ss_* $,
$ ss_* $
|
| $ sw_* > ww_* > ss_* > ws_1 > ws_2 $, and $ 2ww_* < sw_* + ws_1 $ |
How to read these symbols: the subscript is the player who gets the payoff, the first letter is their move, and the second letter is the other player's move. If the subscript is $ * $, then this combination is symmetric. So $ ws_1 $ is the payoff to Player 1, if he Works while Player 2 Shirks. $ ws_2 $ is the payoff to Player 2, if she Works while Player 1 Shirks. $ ws_* $ is both of these values, when they're equal to each other. And to be clear, when they're equal, $ ws_1 $ can stand in for $ ws_* $ just as easily as the other way around.
To help make the structure more visible, I've colored the symbols in green or red according to local incentive gradients - green for "this player prefers this outcome to the outcome they get from changing their move", red for the opposite of that. So when $ ws_1 $ is red, that means $ ss_1 > ws_1 $, since $ ss_1 $ represents Player 1's payoff if he changes his move while Player 2 keeps hers the same. A quadrant is a Nash equilibrium (meaning "neither player wants to change their move unilaterally") iff it has two green symbols. I've also given a slightly darker background to the socially optimal quadrants.
Comparing these games, Ellickson claims for example that norms will tend to punish someone who Shirks in a Prisoner's Dilemma, rather than rewarding those who Work, because eventually most people will Work and it's cheaper to sanction the thing that happens rarely. But in a Specialized Labor game, norms will tend to reward the efficient worker ("cheapest labor-provider") for Working, because that encourages people to obtain the skills necessary to perform this work. There's a background level of skills that everyone is expected to have, and people are punished for falling short of them and rewarded for exceeding them.
So most of the points I want to ding Ellickson here are because this is kind of a strange choice of games. For one thing, it seems to assume that: teaming up to work is more expensive than working individually, iff players have unequal skill levels.
Honestly I don't think that's so implausible as a heuristic. I think "most work projects have gains from working together" is a decent guess, and then one way to remove those gains could be if one player is much more skilled than the other. Still, Ellickson doesn't make this argument, or acknowledge that the assumption is kind of weird.
Another way to justify the omission is if the ommitted possibilities don't add much of interest. Prisoner's Dilemma and Specialized Labor are opposite corners in a two-by-two grid parameterized by "synergistic/discordant" (gains or no gains from cooperation) and "symmetrical/asymmetrical". If our tools for working with them can also be applied to the other corners without much extra effort, then there's no need to consider the others in detail. More on this later.
Something weird on the face of it is that in Specialized Labor, Work/Work results in the same payoff to both players. Why assume that that's symmetrical? But I don't think this is a big deal. Plausibly people can calibrate how hard they work if they think they're getting a worse result than the other. Also I suspect you just don't change much by allowing it to be asymmetrical, provided that both payoffs are in between $ sw_* $ and $ ss_* $.
Similarly you might suppose that the efficient worker doesn't just pay less to Work than the inefficient worker, he also does a better job. In which case we might want to set $ sw_1 < sw_2 $. But again, I doubt that matters much.
Here's my largest objection: Ellickson doesn't consider that work might be worth doing selfishly. In both games, you maximize your own outcome by Shirking, and if that means the work doesn't get done, so be it. But that puts a narrow band on the value of a piece of work. From a social perspective, it's not worth doing for the benefits it gives to one person, but it is worth doing for the benefits it gives to two. I think a lot of the situations Ellickson looks at don't really fit that model. For example, building a fence seems like something you'd often do of your own accord, simply for the benefits it gives to yourself, but Ellickson considers it a Prisoner's Dilemma because most people have the relevant skills. (He doesn't analyse whether fence-building is more easily done in tandem.)
To model this possibility, we'd set $ ws_1 > ss_* $, and maybe $ ws_2 > ss_* $ as well. This gives the game that I like to call the Farmer's Dilemma and others call Chicken, Hawk/Dove or Snowdrift. (Here's why I call it that.) Normally I think of the Farmer's Dilemma as symmetrical, but the asymmetrical case seems fine to count as an instance of it, at least right now.
The tricky thing about this game is that even though you'd be willing to do the work yourself if no one else benefitted, the fact that someone else does benefit makes you want them to join in and help with the work. If they decline,
your only in-game way to punish them is not to do the work, which hurts you too - but if you don't punish them, you're a sucker. This is fundamentally different from the tricky thing with Prisoner's Dilemma and Specialized Labor, which in both cases is simply that people have no selfish incentive to work. So it seems like an important omission. Especially because depending on the exact payoffs, it may be that "one player is a sucker while the other makes out like a bandit" is both a Nash equilibrium and socially optimal.
The thesis of the book is to propose a certain hypothesis. Roughly speaking, and for the purpose of this essay, we can assume the hypothesis says: norms will evolve to maximize the aggregate welfare of the players.
(And so Farmer's Dilemmas might be a good place to look for failures of the hypothesis. When the socially optimal result is for one player to be a sucker, and that's also a Nash equilibrium, the hypothesis thinks this is fine. Humans might not think that, and norms might evolve that the hypothesis would have ruled out. But note that this is only the case in the Discordant Farmer's Dilemma - when there are no gains from cooperation. In the Synergistic Farmer's Dilemma, the socially optimal result is for both players to Work. The Discordant Farmer's Dilemma might be rare in practice - I wouldn't expect it with fence-building, for example.)
Let's pretend we're creating a system of norms for these games. Something we can do is mandate transfers of welfare between players. In each quadrant, we can take some of one player's payoff and give it to the other. Total payoff stays the same, and so the socially optimal outcome stays in the same place. But the distribution of welfare changes, and the Nash equilibria might move.
How do we encourage the socially optimal result by doing this? This is Ellickson's possible minor contribution. He points out that we can do it by introducing a debt from those who Shirk to those who Work, and that the value $ ww_* - ws_1 $ works in both these games.
He calls this the "liquidated-Kantian formula" but doesn't explain the name, and I have only a vague understanding of where he might be going with it. Since the name hasn't caught on, I'm going to propose my own: counterfactual compensation. If I Shirk, I compensate you for your losses compared to the world where I worked.
(To compare: actual compensation would be compensating you for the losses you actually suffered from working, $ ss_* - ws_1 $. Actual restitution would be handing over to you the gains I got from your work, $ sw_* - ss_* $. Counterfactual restitution would be handing over to you the gains I got from not working myself, $ sw_* - ww_* $. Each of these takes one player's payoff in one quadrant, and subtracts the same player's payoff in an adjacent quadrant. Compensation is about your costs, and restitution is about my gains. The actual variants are about differences between the world where no one worked and the worlds where one of us worked; they're about the effects of work that actually happened. The counterfactual variants are about the differences between the worlds where only one of us worked and the world where we both worked; they're about the effects of work that didn't happen.)
(Also: yes, obviously there are caveats to apply when bringing this formula to the real world. Ellickson discusses them briefly. I'm going to ignore them.)
If we apply this formula to the Prisoner's Dilemmma, we get this:
| Prisoner's Dilemma with counterfactual compensation |
|
|
Player 2 |
|
|
Work |
Shirk |
| Player 1 |
Work |
$ ww_* $,
$ ww_* $
|
$ ww_* $,
$ sw_* + ws_* - ww_* $
|
| Shirk |
$ sw_* + ws_* - ww_* $,
$ ww_* $
|
$ ss_* $,
$ ss_* $
|
| $ sw_* > ww_* > ss_* > ws_* $, and $ 2ww_* > sw_* + ws_* $ |
Since $ ww_* > sw_* + ws_* - ww_* $, this puts the incentives in the correct place. The Nash equilibrium is now for both players to Work, which is socially optimal.
(In my taxonomy, depending on whether $ sw_* + ws_* - ww_* ≷ ss_* $, this new game is at the point where The Abundant Commons meets either Cake Eating or Studying For a Test. It's not unique in either case, because there are at most three distinct payout values.)
Specialized Labor is more complicated. There are three ways we might decide to apply counterfactual compensation. We could say that the Shirker compensates the Worker for the Worker's costs, either $ ww_* - ws_1 $ or $ ww_* - ws_2 $ depending on who Worked. Or we could say that the Shirker compensates the Worker for what the efficient Worker's costs would have been, $ ww_* - ws_1 $ regardless of who Worked. Or we could say that the efficient worker never owes anything to the inefficient worker; he gets to just say "sorry, I'm not going to pay you for work I could have done more easily". Lets call these approaches "actual-costs", "efficient-costs" and "substandard-uncompensated"
Ellickson doesn't discuss these options, and I ding him another point for that. He just takes the substandard-uncompensated one. Here's what it looks like.
| Specialized Labor with counterfactual compensation (substandard-uncompensated) |
|
|
Player 2 |
|
|
Work |
Shirk |
| Player 1 |
Work |
$ ww_* $,
$ ww_* $
|
$ ww_* $,
$ sw_* + ws_1 - ww_* $
|
| Shirk |
$ sw_* $,
$ ws_2 $
|
$ ss_* $,
$ ss_* $
|
| $ sw_* > ww_* > ss_* > ws_1 > ws_2 $, and $ 2ww_* < sw_* + ws_1 $ |
Player 2 has no incentive to Work, regardless of what Player 1 does, because $ ss_* > ws_2 $ and (unlike in the Prisoner's Dilemma) $ sw_* + ws_1 - ww_* > ww_* $. And given that Player 2 is Shirking, Player 1 has incentive to Work. So again, we've moved the Nash equilibrium to the socially optimal quadrant.
This isn't, like, a mind-shattering result that's going to blow open the field of game theory. But I don't remember seeing it before, and Ellickson doesn't attribute it to anyone else. I'm inclined to give him some credit for it. Even if others have had the insight before - which I expect they have - it seems like he's still doing competent work in a field outside his own. Not amazing work, not particularly difficult work, but competent.
One objection: the inefficient worker gets a better result than the efficient worker. That seems bad to me, because it discourages people from becoming the efficient worker. I don't think this is a big deal, though. For one thing, acquiring skills probably does increase your own payoff; your skills will feed into $ ww_* $, not just your $ ws $. (So it directly increases your payoff in Work/Work, and reduces your debt in Shirk/Work.) Someone else acquiring skills will increase your payoff even more, perhaps, but that's not a big problem. For another thing, such incentives can be handled out-of-game. I do think Ellickson should have acknowledged this issue, and I ding him a point for not doing so. But a brief note would have been fine.
What happens if we apply counterfactual compensation in the other possible ways? The only difference is in the bottom left quadrant, which becomes either $ sw_* + ws_2 - ww_* $, $ ww_* $ (actual-costs) or $ sw_* + ws_1 - ww_* $, $ ww_* + ws_2 - ws_1 $ (efficient-costs). The problem with both of these is that that quadrant might now be a Nash equilibrium. In the first case, Player 1 might prefer that quadrant over Work/Work, depending on $ 2ww_* ≷ sw_* + ws_2 $, and Player 2 will certainly prefer it over Shirk/Shirk. In the second case, Player 1 will certainly prefer that quadrant over Work/Work, and Player 2 might prefer it over Shirk/Shirk, depending on $ ww_* + ws_2 - ws_1 ≷ ss_* $. That's not great, we only want a Nash equilibrium in the socially optimal quadrant.
On the other hand, I note that if $ ws_1 - ws_2 $ is small, then the social cost is low; and if it's large, then (except perhaps with some fairly specific payoff values?) that quadrant isn't a Nash equilibrium. Meanwhile, if payoffs are uncertain - if people might disagree about who the more efficient worker is - then either of the other choices seems more robust. And this is more of an aesthetic judgment, but it feels like the kind of aesthetic judgment that sometimes hints at deeper problems: there's something a bit weird about how substandard-uncompensated is discontinuous. A small change in Player 2's skills lead to a small change in her compensation in each quadrant, until she gets equally skilled as Player 1, at which point there's a large change in the Shirk/Work quadrant.
On the other other hand, a feature of how these games translate to the real world is that players encourage each other to discuss in advance. Someone building unilaterally may not get to claim this debt. So if they disagree about who the efficient worker is, that's unlikely to cause much grief.
What about measures other than counterfactual compensation? Actual compensation ($ ss_* - ws_1 $) doesn't work. If a player expects the other to Shirk, they'd be indifferent to Working; and in a Prisoner's Dilemma, if they expect the other to Work, they might prefer to Work or not depending on $ ww_* ≷ sw_* + ws_1 - ss_* $. (In Specialized Labor, that inequality always resolves as $ < $ which gives the incentives we want.)
Actual restitution ($ sw_* - ss_* $) is sometimes okay in a Prisoner's Dilemma, but if $ ws_* + sw_* < 2ss_* $ then Shirk/Shirk remains a Nash equilibrium; players will only want to Work if they expect the other to also Work. In Specialized Labor it has the problem that players would prefer to Work than to pay restitution, and so Work/Shirk cannot be a Nash equilibrium.
Counterfactual restitution ($ sw_* - ww_* $) has much the same problem in a Prisoner's Dilemma; if $ ws_* + sw_* < ww_* + ss_* $ then Shirk/Shirk is a Nash equilibrium. And in both games, a player who expects the other to Work will be indifferent to Working.
There are other options for payment one might consider; I haven't even looked at all of them of the form "one raw payoff minus another raw payoff". But so far, counterfactual compensation seems like the best option.
(We could even consider values of the debt based on information outside of the original payoff matrix. But Ellickson points out that when deciding how to act in the first place, players will already want to figure out what the payoff matrix looks like. If the debt was based on other information, there'd be a further cost to gather that information.)
While we're here, let's look at the other games implied by Prisoner's Dilemma and Specialized Labor. The Asymmetrical Prisoner's Dilemma (or Synergistic Specialized Labor) has $ ws_1 ≠ ws_2 $ but $ 2ww_* > ws_1 + sw_* $. In this case, counterfactual compensation does exactly what we want it to do, just like in the symmetrical Prisoner's Dilemma; except that substandard-uncompensated is no good, it doesn't give us a Nash equilibrium at all. (Player 1 prefers Shirk/Work to Work/Work, and Work/Shirk to Shirk/Shirk. Player 2 prefers Work/Work to Work/Shirk, and Shirk/Shirk to Shirk/Work.) If Ellickson had considered this game, he'd have had to discuss the possible ways one might apply counterfactual compensation, which would have been good. So I ding him a point for it.
Symmetrical Specialized Labor (or Discordant Prisoner's Dilemma, or Too Many Cooks) has $ ws_1 = ws_2 $ but $ 2ww_* < ws_* + sw_* $. The difficulty here is that there's no way to break the symmetry. Any of the three ways to apply counterfactual compensation will be equivalent, and leave us with two Nash equilibria in the two socially equal quadrants. The "discuss in advance" feature saves us again, I think; players don't need to somehow acausally cooperate to select one to Work and one to Shirk, they can just, like, talk about it. So I think it was basically fine for Ellickson to not consider this game, though it would have been worth a brief note.
How does this work in the Farmer's Dilemma? First we need to clarify exactly what set of games that refers to. In symmetrical games, I think of it as having $ sw_* > ww_* > ws_* > ss_* $; that is, each player would prefer the other to do all the work, or failing that to help; but they'd still rather do it all themselves than for the work not to get done.
I'm going to break symmetry by separating $ ws_1 $ from $ ws_2 $ as before. Without loss of generality, we can specify $ ws_1 > ws_2 $, but I'm not going to decide whether $ ws_2 ≷ ss_* $. It might be that only one player is skilled enough to benefit from Working alone.
So in normal form, the Farmer's Dilemma looks like this:
| Farmer's Dilemma |
|
|
Player 2 |
|
|
Work |
Shirk |
| Player 1 |
Work |
$ ww_* $,
$ ww_* $
|
$ ws_1 $,
$ sw_* $
|
| Shirk |
$ sw_* $,
$ ws_2 $
|
$ ss_* $,
$ ss_* $
|
| $ sw_* > ww_* > ws_1 > ss_*$, and $ ws_1 > ws_2 $ |
Either of the top two quadrants could be socially optimal, depending whether the game is synergistic or discordant (that is, whether $ 2ww_* ≷ sw_* + ws_* $). Shirk/Work may or may not be a Nash equilibrium, depending whether $ ws_2 ≷ ss_* $. So how does it look with counterfactual compensation? I'll consider the synergy and discord cases separately.
| Synergistic Farmer's Dilemma with counterfactual compensation (substandard-uncompensated) |
|
|
Player 2 |
|
|
Work |
Shirk |
| Player 1 |
Work |
$ ww_* $,
$ ww_* $
|
$ ww_* $,
$ sw_* + ws_1 - ww_* $
|
| Shirk |
$ sw_* $,
$ ws_2 $
|
$ ss_* $,
$ ss_* $
|
| $ sw_* > ww_* > ws_1 > ss_*$, $ ws_1 > ws_2 $, and $ 2ww_* > sw_* + ws_1 $ |
Oh dear. Substandard-uncompensated compensation is clearly not going to work; Shirk/Work might still be a Nash equilibrium. In Specialized Labor it was fine that the efficient Worker would prefer the inefficient Worker to do all the work, because the inefficient worker would say "nuts to that". In a Farmer's Dilemma she might continue to Work, which we don't want. Even if we specified $ ws_2 < ss_* $, we'd simply have no Nash equilibrium; like in the Asymmetrical Prisoner's Dilemma, one player would always get a better result by changing their move.
Fortunately, either of the others seems fine. The payoffs for these are the same as in Specialized Labor, but their values have changed relative to adjacent quadrants. Actual-costs gives us $ sw_* + ws_2 − ww_* $, $ ww_* $ in that quadrant, which isn't a Nash equilibrium because $ ww_* > sw_* + ws_2 − ww_* $. (Compared to this quadrant, Player 1 would rather Work and Player 2 would rather Shirk.) And efficient-costs again gives us $ sw_* + ws_1 − ww_* $, $ ww_* + ws_2 - ws_1 $, which isn't a Nash equilibrium because $ ww_* > sw_* + ws_1 − ww_* $. (Player 1 would still rather Work. Player 2 may or may not prefer to Shirk; if $ ws_2 > ss_* $ she'll certainly prefer this quadrant, might prefer it even if not, but it's not a problem either way.)
What about the discordant case? If $ ws_2 < ss_* $ we actually already have the desired result. The only Nash equilibrium is Work/Shirk which is socially optimal. But as discussed above, it's a crap result for Player 1, and my sense is that the "no incentive to become the efficient worker" problem now becomes a lot more of an issue. Let's see what happens with counterfactual compensation.
| Discordant Farmer's Dilemma with counterfactual compensation (substandard-uncompensated) |
|
|
Player 2 |
|
|
Work |
Shirk |
| Player 1 |
Work |
$ ww_* $,
$ ww_* $
|
$ ww_* $,
$ sw_* + ws_1 - ww_* $
|
| Shirk |
$ sw_* $,
$ ws_2 $
|
$ ss_* $,
$ ss_* $
|
| $ sw_* > ww_* > ws_1 > ss_* $, $ ws_1 > ws_2 $, and $ 2ww_* < sw_* + ws_1 $ |
Again, substandard-uncompensated doesn't really help; Shirk/Work will be a Nash equilibrium iff it was one before. But at least Player 1 gets a less-bad result from Work/Shirk. (Player 2 still does better than him.)
Actual-costs might also be a Nash equilibrium in that quadrant, if $ ww_* < sw_* + ws_2 − ww_* $. And so might efficient-costs, if $ ww_* + ws_2 - ws_1 > ss_* $. (Again, this always holds if $ ws_2 > ss_* $, so looking only at the Nash equilibria, this is strictly worse than having no compensation.)
So this is unfortunate. We can't reliably remove that Nash equilibrium with counterfactual compensation. Depending how we apply it, we might even make it an equilibrium when it wasn't before.
(Actual restitution also works in the synergistic game, but moves the Nash equilibrium to Work/Work in the discordant game. Counterfactual restitution makes players indifferent to Working if they expect their partner to Work, so in practice I guess Work/Work is the Nash equilibrium there, too. And actual compensation would be negative, which is silly.)
Summing up, counterfactual compensation:
- Gives people good incentives in Prisoner's Dilemma. In an Asymmetrical Prisoner's Dilemma, substandard-uncompensated doesn't work.
- Gives people good incentives in Specialized Labor, using substandard-uncompensated. Mostly-good incentives using the other implementations.
- Gives people good incentives in the Synergistic Farmer's Dilemma, except that substandard-uncompensated only works sometimes.
- Maybe kinda sorta helps a bit in the Discordant Farmer's Dilemma. Maybe not.
So that's not amazing. I do think the Discordant Farmer's Dilemma is just fundamantally, in technical terms, a real bastard of a game. But even in the synergistic variant, the way we calibrate it to get the best incentives is different from the way we calibrate it for the best incentives in Specialized Labor.
So I appreciate Ellickson's contribution, and I think it's a real one. But it's not as much as we might have hoped. I think he had a blind spot about the Farmer's Dilemma, and his tools don't really work against it. He also would have done well to consider counterfactual compensation schemes other than substandard-uncompensated.
With counterfactual compensation in mind, Ellickson proposes a variant Iterated Prisoner's Dilemma tournament, and a strategy for it that he calls "Even-Up". Even-Up takes advantage of features of the tournament that make it more realistic, and is modelled on real-world behaviours that he describes elsewhere in the book.
The tournament has rounds of both Prisoner's Dilemma and Specialized Labor, and payoffs for them can vary considerably. He suggests that perhaps one in five rounds might have each payoff increased twentyfold. Additionally, in between rounds, players can unilaterally choose to make a side payment to their partner.
To apply the Even-Up strategy, a player would use an internal balance to keep account of standing with their partner. Whenever counterfactual compensation would be owed, according to the analysis above, they'd adjust the balance by its value. (Ellickson doesn't specify, but presumably they'd also adjust whenever their partner makes a payment to them.) Whenever the balance was close to zero, they'd play the socially optimal strategy. If they were in debt, they'd make a side payment. And if they were in credit, they'd "exercise self-help": Shirk when they'd otherwise Work. (But only if the debt owed was more than half the value of the compensation, so that the balance would become closer to zero.)
There are three parameters I might be inclined to play with. One: which variant of counterfactual compensation should we use? (Ellickson's wording doesn't make it clear which he intends. Above he took substandard-uncompensated for granted, but is wording here sort of hints ambiguously at efficient-costs. He doesn't note or justify the change if there is one.) As noted, substandard-uncompensated gives the right incentives where the other options sometimes don't. Still, I wouldn't be surprised if the other options sometimes helped to avoid a feud (a loop of mutual defections or alternating defections).
Related, two: suppose we do use substandard-uncompensated. When in credit, and facing a Specialized Labor game as the efficient worker, should we Shirk? (Since we'd never Work as the inefficient worker, this is the only time the choice of counterfactual compensation variants is relevant.) Regardless of the other player's move, no compensation is owed. So Shirking will destroy communal resources, but not bring players' standings back in balance. On the other hand, it does stop us from extending more credit that may never be paid back. It may be worth having a higher threshold for this than for Shirking in a Prisoner's Dilemma, but I'd say never Shirking in this case would be a mistake.
And three: is "brings the balance closer to zero" the optimal condition to use for when to exercise self-help? If we exercise it more readily, others may be more inclined to cooperate with us in the first place, but that effect is probaby minor - there's only so much we can be exploited for, over the whole game. On the other hand, we're also destroying more total payoff, per round. It may be worth only exercising self-help if our credit is more than say three-quarters the value of counterfactual compensation.
(If we're looking at modfications to the tournament: as well as tweaking the probability distribution of the various possible payoff matrices, I'd be interested to see what changes if you add a small or large transaction fee to the side payments. Naturally I'd also like to see what happens if you add the possibility of Farmer's Dilemmas, but then Even-Up needs to be altered to account for it. Of other games in the genre, a Discordant Abundant Commons ($ ws_1 > ww_* > \{ sw_*, ss_* \} $, $ 2ww_* < ws_1 + sw_* $, and I'm not sure what the constraints on $ ws_2 $ should be) would also be a good addition. Maybe an asymmetrical Anti-Coordination variant, with a single socially optimal outcome so as not to confuse SociallyOptimalOutcomeBot. The others don't seem like they'd add much; they all have $ ww_* $ as the highest payoff, so their socially optimal outcomes are also individually optimal. That doesn't mean there's no reason not to play Work, but the reasons mostly boil down to "I'm willing to hurt myself to threaten or punish you" and you already get that from the Farmer's Dilemma. So I'm not convinced the other games add much strategic depth, and they do add noise.)
Ellickson predicts that Even-Up would do well in this tournament, and I agree. It's inexploitable, rewards its partners for cooperating, forgives past transgressions, and plays well against itself. I'd be concerned about what happens if it plays against some similar strategy with different ideas of fairness - might you get into a situation where only one of them is ever satisfied at a time, leading to alternating defections? More generally I just don't trust either myself or Ellickson to have especially reliable intuitions about this.
Ellickson also says that if Even-Up turns out not to be evolutionary stable - that is, if a society of Even-Up players can be exploited by other strategies, or wouldn't be able to enter groups currently dominated by other strategies - his hypothesis would no longer be credible. I think it would be stable, but even if not, I'd be somewhat forgiving. I'd want to know why not, before deciding how it reflects on the hypothesis.
Posted on 14 November 2020
|
Comments
The reason that the rich were so rich, Vimes reasoned, was because they managed to spend less money.
Take boots, for example. He earned thirty-eight dollars a month plus allowances. A really good pair of leather boots cost fifty dollars. But an affordable pair of boots, which were sort of OK for a season or two and then leaked like hell when the cardboard gave out, cost about ten dollars. Those were the kind of boots Vimes always bought, and wore until the soles were so thin that he could tell where he was in Ankh-Morpork on a foggy night by the feel of the cobbles.
But the thing was that good boots lasted for years and years. A man who could afford fifty dollars had a pair of boots that'd still be keeping his feet dry in ten years' time, while the poor man who could only afford cheap boots would have spent a hundred dollars on boots in the same time and would still have wet feet.
This was the Captain Samuel Vimes 'Boots' theory of socioeconomic unfairness.
– Terry Pratchett, Men at Arms
This is a compelling narrative. And I do believe there's some truth to it. I could believe that if you always buy the cheapest boots you can find, you'll spend more money than if you bought something more expensive and reliable. Similar for laptops, smartphones, cars. Especially (as Siderea notes, among other things) if you know how to buy expensive things that are more reliable.
But it's presented as "the reason that the rich [are] so rich". Is that true? I mean, no, obviously not. If your pre-tax income is less than the amount I put into my savings account, then no amount of "spending less money on things" is going to bring you to my level.
Is it even a contributing factor? Is part of the reason why the rich are so rich, that they manage to spend less money? Do the rich in fact spend less money than the poor?
That's less obvious, but I predict not. I predict that the rich spend more than the poor in total, but also on boots, laptops, smartphones, cars, and most other things. There might be exceptions where rich people consume less of the thing than poor people - bus tickets, for example - but I think if you group spending in fairly natural ways, the rich will spend more than the poor in almost every group.
-
Maybe they spend less money on their daily wear boots, but own more pairs of shoes for different occasions. Or maybe they decide that they care about other things than lifetime cost for their daily wear boots, and spend more on those, too. (Being rich means they can afford to care about other things than lifetime cost.)
-
Apparently famous people often get comped meals, but I bet most of them still spend more money on food than I do.
-
I spent £500 on a laptop in 2013, and before that, £300 in 2008. If I'd gone for £200 laptops each time, maybe they would only have lasted two years each. But if I weren't a techno-masochist, maybe I'd realize that using old laptops actually kind of sucks, and I'd upgrade far more often. My work laptop, bought by people who want me to be maximally effective at my job, cost over £1000 and isn't going to last ten years.
-
Financial services are a case where I'd guess the rich and the poor spend money on very different things. I assume the rich don't have to pay to cash a cheque, and very rarely visit loan sharks. But the poor rarely have Amex Platinum cards ($550/year), or personal accountants. (Maybe it's unfair to count those because they save you money in other areas?)
-
Buying a house may be cheaper in the long run than renting a similar house nearby. But rich people tend to live in nicer houses and/or nicer areas.
Those are all guesses. I don't have good data on this, and I'd love to see it if you do.
For what data I do have, the first google result was this page from the UK's Office of National Statistics. Specifically, look at figure 4, "Indexed household income, total spending and spending by component by income decile, UK, FYE 2019".
They split households into ten income levels, and look at four categories of spending plus total spending. Each of those is a near-strictly increasing line from "poor people spend less" to "rich people spend more". (I see two blips: the 90th percentile of income spends slightly less on housing than the 80th, and the 70th spends slightly less on food and non-alcoholid drinks than the 60th. The other categories are transport, and recreation and culture. These four are the largest spending categories on average across all income levels. The graph also has disposable income, which I think is irrelevant for current purposes.)
(I repeat that this specific data is not strong evidence. The source for it is the living costs and food survey, which might have more detail. (Link goes to the previous year's version because that's what I could find.) Unfortunately it's not open access. It might be freely available if I register, but I don't care enough to try right now. In any case, we'd also want data from outside the UK.)
There will obviously be some exceptions. There will be some rich people who spend less money than some poor people. There will probably even be some rich people who spend less money than some poor people, and would not be rich otherwise. But as a general theory for why the rich are rich? I just don't buy it.
I believe boots theory points towards one component of socioeconomic unfairness. But boots theory itself is supposed to be a theory of why the rich are so rich. It's very clear about that. It's clearly wrong, and I predict that even a weakened version of it is wrong.
To be a little more precise, I think boots theory as written makes three increasingly strong claims, that we could think of as "levels of boots theory":
- Being rich enables you to spend less money on things. (More generally: having incrementally more capital lets you spend incrementally less money. Also, being rich is super convenient in many ways.) This phenomenon is also called a ghetto tax.
- Also, rich people do in fact spend less money on things.
- Also, this is why rich people are rich.
All of these levels have stronger and weaker forms. But I think a quick look at the world tells us that the first level is obviously true under any reasonable interpretation, and the third level is obviously false under any reasonable interpretation. The second I predict is "basically just false under most reasonable interpretations", but it's less obvious and more dependent on details. There may well be weak forms of it that are true.
It may be that most people, when they think of boots theory, think only of levels one or two, not level three. I don't know if you can read this quora thread that I found on Google. It asks "How applicable to real life is the Sam Vimes "Boots" Theory of Economic Injustice?" The answers mostly agree it's very applicable, but I think most of them are on level one or two. (The one talking about leverage seems like level three, if it's talking about boots theory at all. I'm not convinced it is.)
But it seems to me that boots theory is usually presented in whole in its original form. Its original form is succinct and well written. When people want to comment on it, they very often include the very same quote as I did. And the original form starts by very clearly telling us "this is a theory of why the rich are so rich". It is very obviously level three, which is very obviously wrong.
So I have a few complaints here.
One is, I get the impression that most people don't even notice this. They link or quote something that starts out by saying very clearly "this is a theory of why the rich are so rich", and they don't notice that it's a theory of why the rich are so rich.
(I wouldn't be too surprised (though this is not a prediction) if even the author didn't notice this. Maybe if you had asked him, Terry Pratchett would have said that no, obviously Sam Vimes does not think this is why the rich are so rich, Sam Vimes just thinks this is a good illustration of why it's nice to be rich.)
This disconnect between what a thing actually says, and what people seem to think it says, just bothers me. I feel the desire to point it out.
Another is, I think there's a motte-and-bailey going on between levels one and two. A quora commenter says it's "far more expensive to be poor than it is to be rich, both in a percentage of income respect and a direct effect". He gives examples of things that rich people can spend less money on, if they choose. He doesn't provide data that rich people do spend less money on these things. Another describes how being rich lets you save money on food staples by stocking up when there's a sale. He doesn't provide data that rich people do spend less money on food or even staples. You could certainly make the case that neither of these people is explicitly claiming level two. But I do think they're hinting in that direction, even if it's not deliberate.
And relatedly: if we want to help people escape poverty, we need to know on what levels boots theory is true or false. If we want to know that, we need to be able to distinguish the levels. If "boots theory" can refer to any of these levels, then simply calling boots theory "true" (or even "false") is uninformative. We need to be more precise than that. To be fair, the quora commenters make specific falsifiable claims, which is commendable. But the claims are meant to be specific examples of a general phenomenon, and the general phenomenon is simply "boots theory", and it's not clear what they think that means.
I advise that if you talk about boots theory, you make it clear which level you're talking about. But maybe don't use that name at all. If you're talking about level one, the name "ghetto tax" seems fine. If you do want to talk about levels two or three, I don't have a good altiernative name to suggest. But since I don't think those levels are true, I'm not sure that's a big problem.
Update 18 Mar 2025: This post has a followup, Boots theory and Sybil Ramkin.
Update 1 Aug 2025: And another followup, Boots theory and Wikipedia.
Posted on 14 September 2020
|
Comments
Consider games with the following payoff matrix:
| |
|
Player 2 |
|
| |
|
Krump |
Flitz |
| Player 1 |
Krump |
$(W, W)$ |
$(X, Y)$ |
| |
Flitz |
$(Y, X)$ |
$(Z, Z)$ |
One such game is the Prisoner's Dilemma (in which strategy "Krump" is usually called "Cooperate", and "Flitz" is usually called "Defect"). But the Prisoner's Dilemma has additional structure. Specifically, to qualify as a PD, we must have $Y > W > Z > X$. $Y > W$ gives the motivation to defect if the other player cooperates, and $Z > X$ gives that motivation if the other player defects. With these two constraints, the Nash equilibrium is always going to be Flitz/Flitz for a payoff of $(Z, Z)$. $W > Z$ is what gives the dilemma its teeth; if instead $Z > W$, then that equilibrium is a perfectly fine outcome, possibly the optimal one.
I usually think of a Prisoner's Dilemma as also having $2W > X + Y > 2Z$. That specifies that mutual cooperation has the highest total return - it's "socially optimal" in a meaningful sense - while mutual defection has the lowest. It also means you can model the "defect" action as "take some value for yourself, but destroy value in the process". (Alternatively, "cooperate" as "give some of your value to your playmate, adding to that value in the process".) We might consider instead:
- If $2W < X + Y$, then defecting while your playmate cooperates creates value (relative to cooperating). From a social perspective, Krump/Flitz or Flitz/Krump is preferable to Krump/Krump; and in an iterated game of this sort, you'd prefer to alternate $X$ with $Y$ than to get a constant $W$. Wikipedia still classes this as a Prisoner's Dilemma, but I think that's dubious terminology, and I don't think it's standard. I might offhand suggest calling it the Too Many Cooks game. (This name assumes that you'd rather go hungry than cook, and that spoiled broth is better than no broth.)
- If $2Z > X + Y$, then defecting while your playmate defects creates value. I have no issue thinking of this as a Prisoner's Dilemma; my instinct is that most analyses of the central case will also apply to this.
By assigning different values to the various numbers, what other games can we get?
As far as I can tell, we can classify games according to the ordering of $W, X, Y, Z$ (which determine individual outcomes) and of $2W, X + Y, 2Z$ (which determine the social outcomes). Sometimes we'll want to consider the case when two values are equal, but for simplicity I'm going to classify them assuming there are no equalities. Naively there would be $4! · 3! = 144$ possible games, but
- Reversing the order of everything doesn't change the analysis, it just swaps the labels Krump and Flitz. So we can assume without loss of generality that $W > Z$. That eliminates half the combinations.
- Obviously $2W > 2Z$, so it's just a question of where $X + Y$ falls in comparison to them. That eliminates another half.
- If $W > Z > • > •$ then $X + Y < 2Z$. That eliminates another four combinations.
- If $• > • > W > Z$ then $X + Y > 2W$, eliminating another four.
- If $W > • > • > Z$ then $2W > X + Y > 2Z$, eliminating four.
- If $W > • > Z > •$ then $2W > X + Y$, eliminating two.
- If $• > W > • > Z$ then $X + Y > 2Z$, eliminating two.
That brings us down to just 20 combinations, and we've already looked at three of them, so this seems tractable. In the following, I've grouped games together mostly according to how interesting I think it is to distinguish them, and I've given them names when I didn't know an existing name. Both the names and the grouping should be considered tentative.
Cake Eating: $W > • > • > Z$ (two games)
In this game, you can either Eat Cake or Go Hungry. You like eating cake. You like when your playmate eats cake. There's enough cake for everyone, and no reason to go hungry. The only Nash equilibrium is the one where everyone eats cake, and this is the socially optimal result. Great game! We should play it more often.
(If $X > Y$, then if you had to choose between yourself and your playmate eating cake, you'd eat it yourself. If $Y > X$, then in that situation you'd give it to them. Equalities between $W, Z$ and $X, Y$ signify indifference to (yourself, your playmate) eating cake in various situations.)
Let's Party: $W > Z > • > •$ (two games)
In this game, you can either go to a Party or stay Home. If you both go to a party, great! If you both stay home, that's cool too. If either of you goes to a party while the other stays home, you'd both be super bummed about that.
Home/Home is a Nash equilibrium, but it's not optimal either individually or socially.
In the case $W = Z$, this is a pure coordination game, which doesn't have the benefit of an obvious choice that you can make without communicating.
(Wikipedia calls this the assurance game on that page, but uses that name for the Stag Hunt on the page for that, so I'm not using that name.)
Studying For a Test: $W > X > Z > Y$ (two games)
You can either Study or Bunk Off. No matter what your playmate does, you're better off Studying, and if you Study together you can help each other. If you Bunk Off, then it's more fun if your playmate Bunks Off with you; but better still for you if you just start Studying.
The only Nash equilibrium is Study/Study, which is also socially optimal.
Stag hunt: $W > Y > Z > X$ (two games)
You can either hunt Stag or Hare (sometimes "Rabbit"). If you both hunt Stag, you successfully catch a stag between you, which is great. If you both hunt Hare, you each catch a hare, which is fine. You can catch a hare by yourself, but if you hunt Stag and your playmate hunts Hare, you get nothing.
This also works with $Y = Z$. If $Y > Z$ then two people hunting Hare get in each other's way.
The Nash equilibria are at Stag/Stag and Hare/Hare, and Stag/Stag is socially optimal. Hare/Hare might be the worst possible social result, though I think this game is usually described with $2Z > Y + X$.
See: The Schelling Choice is "Rabbit", not "Stag".
The Abundant Commons: $X > W > • > •$ (five games)
You can Take some resource from the commons, or you can Leave it alone. There's plenty of resource to be taken, and you'll always be better off taking it. But if you and your playmate both play Take, you get in each other's way and reduce efficiency (unless $X = W$).
If $2W > X + Y$ then you don't intefere with each other significantly; the socially optimal result is also the Nash equilibrium. But if $2W < X + Y$ then the total cost of interfering is more than the value of resource either of you can take, and some means of coordinating one person to Take and one to Leave would be socially valuable.
If $Y > Z$ then if (for whatever reason) you Leave the resource, you'd prefer your partner Takes it. If $Z > Y$ you'd prefer them to also Leave it.
An interesting case here is $X > W > Z > Y$ and $X + Y > 2W$. Take/Leave and Leave/Take are social optimal, but the Leave player would prefer literally any other outcome.
Take/Take is the only Nash equilibrium.
In this game, you can Work (pitch in to help build a mutual resource) or Shirk (not do that). If either of you Works, it provides more than its cost to both of you. Ideally, you want to Shirk while your playmate Works; but if your playmate Shirks, you'd rather Work than leave the work undone. The Nash equilibria are at Work/Shirk and Shirk/Work.
If $2W > X + Y$ then the socially optimal outcome is Work/Work, and a means to coordinate on that outcome would be socially useful. If $2W < X + Y$, the socially optimal outcome is for one player to Work while the other Shirks, but with no obvious choice for which one of you it should be.
Also known as Chicken, Hawk/Dove and Snowdrift.
Anti-coordination: $• > • > W > Z$ (two games)
In this game, the goal is to play a different move than your playmate. If $X = Y$ then there's no reason to prefer one move over another, but if they're not equal there'll be some maneuvering around who gets which reward. If you're not happy with the outcome, then changing the move you play will harm your playmate more than it harms you. The Nash equilibria are when you play different moves, and these are socially optimal.
Prisoner's Dilemma/Too Many Cooks: $Y > W > Z > X$ (three games)
Covered in preamble.
(I'm a little surprised that this is the only case where I've wanted to rename the game depending on the social preference of the outcomes. That said, the only other games where $X + Y$ isn't forced to be greater or less than $2X$ are the Farmer's Dilemma and the Abundant Commons, and those are the ones I'd most expect to want to split in future.)
A graph
I made a graph of these games. I only classified them according to ordering of $W, X, Y, Z$ (i.e. I lumped Prisoner's Dilemma with Too Many Cooks), and I drew an edge whenever two games were the same apart from swapping two adjacent values. It looks like this:

source
The lines are colored according to which pair of values is swapped (red first two, blue middle two, green last two). I'm not sure we learn much from it, but I find the symmetry pleasing.
A change of basis?
I don't want to look too deep into this right now, but here's a transformation we could apply. Instead of thinking about these games in terms of the numbers $W, X, Y, Z$, we think in terms of "the value of Player 2 playing Flitz over Krump":
- $α = X - W$, the value to Player 1, if Player 1 plays Krump.
- $β = Y - W$, the value to Player 2, if Player 1 plays Krump.
- $γ = Z - Y$, the value to Player 1, if Player 1 plays Flitz.
- $δ = Z - X$, the value to Player 2, if Player 1 plays Flitz.
These four numbers determine $W, X, Y, Z$, up to adding a constant value to all of them, which doesn't change the games. For example, Prisoner's Dilemma and Too Many Cooks both have $α < 0, β > 0, γ < 0, δ > 0$. A Prisoner's Dilemma also has $α + β < 0$ while Too Many Cooks has $α + β > 0$.
So what happens if we start thinking about these games in terms of $α, β, γ, δ$ instead? Does this give us useful insights? I don't know.
Of course, for these numbers to point at one of the games studied in this post, we must have $α - β = γ - δ$. I think if you relax that constraint, you start looking into games slightly more general than these. But I haven't thought about it too hard.
Posted on 04 July 2020
|
Comments
Sometimes I write things in places that aren't here. Sometimes I think those things are worth preserving. Some of those things follow, with minor editing, mostly on the subject of various movies that I've watched. Also two stage musicals, one TV show, one short story, and one music video. They were written over the past four years, so I can't necessarily talk intelligently about these things any more. When I name a thing, spoilers generally follow.
It seemed like it was going to be a film about a cowboy with a death wish, who should be removed from duty but isn't because of institutional dysfunction in the US army. Or something along those lines.
Instead it turned out to be… a film about a cowboy with a death wish?
Like there's that bit where he's just been a fucking idiot who could have gotten everybody killed
(not very specific so far)
And someone who I got the impression outranks him comes up to him like «oh you seem like hot shit. Just how hot shit are you? Yeah that's pretty hot shit» in a tone that I swear is subtextually «I'm about to rip you a new one»
and then the scene just ends. No one gets ripped a new anything.
What?
His team mates realise how dangerous he is to be around. But they don't do anything about it, just get pissed at him. And also he's supposedly defused almost a thousand bombs. There's tension there, a question of how he hasn't died yet (did he used to be good at his job and recently something happened to make him so reckless?) but the film doesn't acknowledge it, it doesn't seem to think "being a fucking dangerous idiot cowboy" and "successfully defusing almost a thousand bombs" are at all incompatible?
This was a really well regarded movie. It won six Oscars, including best picture, best screenplay and best director. Part of me would be inclined to chalk that up to politics, but the movie isn't even especially political from what I could tell; I'm pretty sure it could have been made both more political and a better movie. So I don't think that's a complete explanation.
I suspect all the praise came for reasons that I missed either because I was distracted by this stuff or because I'm just not into the kind of movie it was trying to be or something. But that's really not very specific.
The Jungle Book (2016) is surprisingly pro-human?
I don't think it was intended, and I might be putting too much of myself into it. But like-
Right up until the climax, tool use is shown as almost unambiguously good. Mowgli bangs rocks together to get a sharp stone to cut vines to make rope so he can climb down a cliff face and knock honeycombs with a stick, armored in clothes he makes. He collects honey on an unprecedented scale. Then he saves an elephant from a pit.
(The music to that scene is "The Bare Necessities", a song about how you should just take life easy and all your needs will be met. Everything you need is right within your reach. The implication seems to be that "using tools to extend your reach" is just the obvious, natural, path-of-least-resistance thing to do?)
And the counterpoint isn't really there, though there's plenty of opportunity. Shere Khan says man isn't allowed in the jungle, but doesn't talk about why. Akela and Bagheera tell Mowgli to act more like a wolf and less like a man, his "tricks" are not the wolf way, but don't say what the problems are with manhood. Kaa shows fire being dangerous, but then with more realism shows fire being used to fight off Shere Khan and save Mowgli's life. Mowgli refuses to give fire to King Louie but doesn't explain his refusal. The elephant could have fallen into a human trap, but instead it was apparently just a pit. And the bees?
From the bees' perspective, I imagine Mowgli is probably terrifying. He knocks down honeycomb after honeycomb and he just keeps going. He's an existential threat to their society and there's nothing they can do about it, though they throw their lives away trying to stop him. I imagine.
But the movie doesn't show that or invite us to think about it. In a world where the animals all talk to each other, the bees are silent. When they sting, it's to teach us about Baloo's trickery and Mowgli's cleverness. They might as well be thistles.
The film has so many opportunities to show or at least tell us that man is destructive, man will kill everyone in the jungle. But it mostly doesn't seem to take them.
So when Mowgli goes to steal fire - well, we know what's going to happen, but only because we already know fire. The movie hasn't given us any particular reason to be scared of it. Also, the mythical associations of stealing fire are fairly pro-fire.
And yes, the fire spreads and Mowgli throws his torch away. But then he fights using some other things humans excel at: coalition-building, getting other people to fight for you, and making a wolf think you're part of its family.
(Here I do think I'm putting in too much of myself. I think the climax is meant to be about winning by combing animal things and man things. The coalition-building is introduced with the law of the jungle, "the strength of the pack is the wolf and the strength of the wolf is the pack". Then Bagheera says "fight him like a man". Then Mowgli says "dead tree" calling back to what Bagheera taught him in the beginning. And in the end Mowgli stays in the jungle. I think that's what is going for, but it's not what I got from it.)
And the fire is put out without too much trouble (when the elephants decide "actually, it would be better if this river went in this direction" and do some engineering works, not done by humans but very human of them), and we haven't actually seen it kill anyone.
So the film roughly seems to be about how the things that separate man from the animals are actually really great. And that's… not what I was expecting.
From memory, Team America was funny and it had decent music. But what made it so great was that while parodying action films, it still managed to be just legitimately good as an action film.
The Book of Mormon was funny and it had decent music.
How many levels of irony is Goodbye Mr A on?
The lyrics are overtly critical of Mr A, but subtextually feel critical of the singers, who dislike him for exposing their flaws to themselves. ("You claim science ain't magic and expect me to buy it"; "you promised you would love us but you knew too much" "so busy showing me where I'm wrong, you forgot to switch your feelings on". And like, "if love is subtraction, your number is up / your love is a fraction, it's not adding up" - I could believe that was written seriously, but I hope not.) And the first part of the video clearly makes out the Hoosiers to be the villains, partly the whole "kidnapping a superhero" thing and partly idk, they just look subtly villainous. Possibly related to camera angles.
But then they go on to take his place, and as far as I can see they do it fine? We only see two of their deeds, but they rescue a cat and stop a burglary. Wikipedia says they fight crime as incompetent antiheros, but I'm not seeing the incompetence. And they become immensely popular.
If we're meant to see them as incompetent, then it reads to me like a criticism of society-at-large; a claim that the singers' narcissism is widespread. But if we're not, then…?
Also relevant: if it's critical of society, or even just the singers, then by extension it's defensive of Mr A. And if Mr A is meant to be identified with the comic book character, it becomes a defense of objectivism, which feels implausible on priors to me. (But maybe it was more likely in 1997? Wizard's First Rule only came out a few years before, I think that was objectivist? By reputation that wikipedia doesn't immediately confirm.)
I've been idly wondering this for over ten years. Today I got around to actually rewatching/relistening to it. It didn't help much.
Wonder Woman has the overt message that ordinary people can't do very much (though not literally nothing). You need someone with super powers to beat up the villain and then everything will be fine. The love interest keeps trying to tell the hero that things are just not that simple, and he keeps getting proved wrong. This message is undercut by the historical realities of WWI.
Matilda has the overt message that ordinary people, even young children, can save the day if they stand up to villainy. Before she gets powers, Matilda tells us that even young kids can do something to make things right, and she turns her dad's hair green and glues his hat on his head. In the climax, the kids revolt against Miss Trunchbull, saying "she can't put us all in chokey". This message is undercut by the fact that all of this is completely ineffectual. Matilda's dad doesn't become any less abusive or criminal. Trunchbull can and does put them all in chokey. What saves the day is someone using super powers to scare Miss Truchbull into running away, and then someone using the Russian mafia to scare the dad into running away.
Face/Off as a retelling of the Gospel narrative
Admittedly I haven't really read the gospels, so maybe I'm completely off base here. But consider:
God (signified by Sean Archer) takes on the form of a sinner (signified by Castor Troy), in order to redeem the sinners. He's pretty successful. Most notably, when Sasha dies, it comes from acting as a force for good, sacrificing herself to save an innocent. She tells Archer not to let her son grow up like him. And so her son (named Adam, signifying Man) grows up in the house of God.
Meanwhile, the Devil (also signified by Castor Troy) attempts to seduce God's followers (Archer's family and colleagues) off of the righteous path, but he's ultimately unsuccessful. People learn to see past outward appearances to what really matters: we know him by his works (the story of his date with Eve). Evil contains the seeds of its own downfall, and Jamie stabs him with the butterfly knife he gave her.
Assorted other thoughts:
"Sean" is derived from John, meaning "God is gracious". Arrows are of course both straight and narrow, signifying the path of God; "Archer" doesn't just follow the path of God, he directs it.
Meanwhile, "Castor" is cognate to (or at least sounds a bit like) "caster", as in a witch; and "Troy" refers to the Trojan war, signifying violence and trickery. Castor's brother is named "Pollux", a decidedly ugly name that sounds a lot like "pox", the plague. According to Wikipedia, Castor and Pollux (brothers of Helen of Troy) spent some time being venerated with Christian saints; and one of them may even have been the basis of John (Sean) the Apostle.
"Adam", as I said before, signifies Man; Archer's daughter is named "Jamie", a gender-neutral name, to ensure we know that God loves his sons and daughters and nonbinary children equally.
Archer's blood type is O-, the "purest" blood type (i.e. fewest antigens in the cells), which gives to all. Troy's is AB (unspecified, so probably AB+), the most "contaminated" type, which takes from all and never gives back. (House has used this same metaphor.)
Canonically, I think Jesus is supposed to get crucified and stabbed with the holy lance. The film has both of these elements, but gets it a bit confused; while Troy is in the classic raised-arms position, Archer shoots him with a harpoon gun.
The final confrontation, in which Good defeats Evil once and for all, is kicked off in a church; symbolically, in The Church, the hearts of God's followers. The battle startles the doves in the church, but we never see a dove die: the peace in our hearts may be disturbed, but will always return.
It's hard to miss the symbolism of Archer breaking out of a hellish prison. (The part of Thomas is briefly played by Jamie, when she shoots him.) The prison being named Erewhon ("nowhere" spelled almost backwards) probably intends to take a position on some Christian point of contention that I'm not familiar with.
You never see the butterfly knife being opened or closed. The cuts are kind of jarring, as if to draw attention to this fact. I think it's trying to tell us something about temptation: we may think we can stray a little, and turn back before we go too far down the wrong path. But by the time we know we're going too far, we've already gone too far. (cf)
This is perhaps the most overtly anti-makeup film I remember seeing ever.
Don't think too hard about the fact that Archer's wife, Adam's adoptive mother, is named Eve.
Hot take: the Saw franchise as exploration of meritocracy
Members of the underclass are given tests. If they pass, they get a new life. Thus, the meritorious are elevated to the elite. Meritocracy!
(Once you've survived a Saw trap, food tastes nicer, your addiction vanishes, you quit the job you hate and get the one you've always dreamed of, puppies and rainbows and so on. I'm not sure how much this is actually shown in the series, but it's what Jigsaw is going for, and the series is much more interesting if it works.)
This would be pretty dumb, but not obviously dumber than some of the other stuff out there.
(Someone on reddit was wondering whether books are worth it. Someone recommended Borges to them, and in particular this story. The version I initially read was a slightly different translation to the one linked. I didn't like the story, but it has the virtue of being considerably shorter than this review.)
I gotta admit, this does not sell Borges to me.
Fair warning, this is gonna come across as fairly dismissive/derisive/antagonistic. I could try to describe my reaction without coming across like that, but it would be hard to do, and especially hard to do honestly.
To me it feels like a short piece of philosophy ("it lay within… the world's contents"), wrapped in some prose.
I don't feel like the prose adds anything to the philosophy. Like for example I don't see it as an illustration of the thing the philosophy is meant to teach us. (If anything, the philosophy is trying to teach us that the prose can't illustrate it.) So if that's all it is, then I'd rather the philosophy be presented by itself, so that I could read it more easily, and comment on it without feeling like someone's going to tell me I'm missing the point.
Commenting on the prose by itself… stylistically, it uses too many words in too few sentences, and feels like a chore to read.
One thing that strikes me is that for Borges to write this story, he must have had the same epiphany as Marino and (maybe) Homer and Dante. Since those are the only people mentioned in relation to the epiphany, it seems that Borges is comparing himself to the three of them. Is that deliberate?
Another thing that strikes me is that if "the motionless and silent act that took place that afternoon" is meant to be "Marino having an epiphany", then we're told that: it happened "on the eve of his death"; that it was "the last thing that happened in his life"; but also that "it was neither that afternoon nor the next that Giambattista Marino died". This seems inconsistent, and given the focus on it, I assume it was intentional. But I have no idea why.
I don't know what the poetry means, or whether the meaning is important.
I could well be missing something here, and whether I am or not I suspect it's partly just a question of taste.
It's an exploration of culture. Ben and Leslie created their own culture and raised their kids in it. The kids have almost no exposure to American culture. Culture Fantastic isn't perfect, and Ben isn't a flawless exemplar of it. There are some things it does better than American culture, and other things it does worse. But it's fine.
But when Culture Fantastic meets American culture, they clash. American kids seem weak, uneducated, not formidable. Fantastic kids seem - weird, socially unskilled, vaguely autistic.
And this should be fine, but none of the adults really respect the other culture. Ben's not especially rude, he knows he's on foreign ground and tries to be respectful to people's faces except when it matters, he just sometimes fails because he's human and hurting. It probably helps that he was probably raised in American culture, too. But he clearly does not approve of the culture. Meanwhile, Leslie's parents give her a Christian funeral, despite her own wishes. Two couples threaten to have the Fantastic kids taken away, because in their eyes, not being raised in American culture means they'll never survive in the real world - by which they mean American culture.
(And no one particularly respects the kids' wishes. That's not a part of either culture. They mostly like Culture Fantastic and want to stay in it, but if they didn't… I think Ben would come around and let them leave, but not easily.)
And it's particularly resonant for me because damn it, I like Culture Fantastic. He's raising those kids to be much like I want to be, even if it causes friction with the world around me.
Sometimes I read things that feel like the author thinks my culture is bad and should be destroyed. My culture is not bad. You do not get to take it away from me.
Captain Fantastic comes down firmly on the side of "not bad", and vaguely-noncomitally on the side of "do not take away".
Act 1: Stick to your principles.
Act 2: War is hell.
Act 3: The War Prayer, but unironically.
(Spoilers only up to season 2.)
Snow is way too forgiving of Regina. Fine, characters are allowed to be silly in boring ways. Snow finally makes the right decision and kills Cora, go her! I don't even mind that she feels guilty about it, though I'd much prefer if that was combined with "but I know it was the right thing to do anyway".
But the world of the show is like, nope! That was objectively wrong of you! Your heart is black now! Fuck you for wanting to protect your family, fuck consequentialism.
And because of her black heart, supposedly she's now inevitably going to go bad and tear apart her family. (That came from Regina, who may have been making it up, but… I'd give at least 3:1 that it pays off.)
Other people are allowed to kill, either without their hearts getting black spots or at least without becoming the sort of people that destroy the people they love. But Snow gets held to a higher standard than everyone else, apparently because she's So Good?
So like, if you're the type of person who kills people, you're allowed to kill people. If you're not the type of person who kills people, but you decide that killing someone is the right thing to do anyway, you're not allowed, and if you do it you become Objectively Bad, unlike people for whom killing is just a thing they do.
And! I don't remember if we've ever definitely seen Snow kill someone yet (at the very least she shot someone with an arrow, it's possible he survived), but she led an army to overthrow two kingdoms! At least one of those kingdoms was her suggestion! People die in war! Even if she hasn't directly killed anyone, she has been responsible for lots of deaths! But those don't count because ???
(And it's not because it was indirect, because Cora was indirect too.)
(It could be because she did it with the candle, but that's not how the narrative is pushing.)
It's like only named characters matter. Not just in the sense that the narrative focuses on them, not just in the sense that the named characters only care about other named characters, those both feel like common mistakes that fiction makes. But as a fundamental moral truth of the universe of the show, which feels less common and more annoying.
There's a related thing where… we met Regina and she's evil, and then we see her backstory and she becomes sympathetic even when she's still evil. (And the same with Rumple, and to some extent with Cora.)
But when she's the Evil Queen she tells her people to kill an entire village and they just do it. Regina has sympathetic motives, but her enforcers are anonymous. We don't see whether they're doing it out of fear, sadism, loyalty, a twisted sense of the greater good, whatever. We've been given a glimpse into the lives of the subjects who hate her, but not the ones who serve her.
(Stanley Glass is an admitted exception, and there was her father, and a brief conversation with a henchman of "I hired you even though you were drunk" or something, but there's really not much.)
Her followers don't get backstories or redemption narratives or people refusing to kill them because There Must Be Another Way. They just get killed, and the narrative doesn't care.
(Compete aside, Regina blames Snow for turning her evil, while Snow credits Regina for turning her good. Neat twist on "I made you? You made me first.")
Posted on 12 June 2020
|
Comments
This is a toy language I've been designing, or at least implementing, for about a year.
It's another take on "Haskell with a Lisp syntax". I'm aware of prior art: Hackett, Axel and Liskell. I haven't looked closely at any of them, because doing that seemed like it might make me less likely to keep working on Haskenthetical.
I call it "toy" in the sense of… well, right now it's a toy like an RC plane is a toy. But my vague goal is to make it into a toy like the Wright flyer would have been a toy if it had been built in 2003. I'd like to get it, say, 80% of the way to being a "real" language. I have no intention or expectation of taking it the other 800% of the way. I have no intention or expectation of taking on responsibility-according-to-me here.
(And honestly, even the first 80% is super ambitious. I don't expect to get that far, it would just be nice to. If I never touch the project again after this, I won't consider my time wasted.)
If you're curious, the source code is available here¶. If you have stack, stack build --fast should suffice to build and then stack exec -- haskenthe -h to run the executable.
So far I've implemented basic Hindley-Milner type inference, the ability to define new types, and pattern matching. The only built-in types are ->, Float (which is a Haskell Double under the hood), and String (a Haskell Text). Builtin functions are +, - and * (all of type -> Float (-> Float Float) and err! (of type -> String $a). I don't yet have division because I haven't decided how I want to handle division by 0. I don't expect I'll come up with anything particularly exciting there, but also I haven't felt the need for division yet.
(Actually, the types Either and , are also builtin, along with functions to work with them: constructors Left, Right and ,, and destructors either, car and cdr. But that's just because I added them before I added custom types, and I haven't bothered to remove them yet.)
I have a long list of things I'd like to include in future. Probably the ones that interest me most right now are macros, extensible records, and compilation. I don't know how macros and compilation are supposed to fit together, but I have some vague ideas in my head. And clearly it's been done in the past, so I assume I can find out how.
Other things include IO, comments, imports, exhaustiveness checking and FFI. Maybe typeclasses, but I'm curious whether macros and lazy evaluation can make those less useful. Maybe lazy evaluation, but I'm on the fence about that.
Open variants (the sum-type version of extensible records) might be on that list too, but I'm not familiar with any prior uses of them so I guess there's probably something that makes them difficult? Maybe they're just not very ergonomic in actual use, in which case cool, they'll fit right in.
What I have so far isn't very interesting as a language, but it might be interesting enough to be worth writing about.
General language overview
There are seven types of expression right now. I'm going to assume you'll understand most of them just by name.
Literal values are Strings and Floats. Variables are bare words with very few restrictions. (Right now they can contain any combination of printable characters other than whitespace, ", ( and ); except that they can't start with something that would parse as a Float.) Lambdas have the syntax (λ (arg1 arg2 ...) expr), or if there's only one argument, (λ arg expr) is also acceptable. Function calls, unsurprisingly, look like (func arg1 arg2 ...), where all of those are expressions.
There are two forms of let-binding. Syntactically they're similar: ([let/letrec] ((name1 expr1) (name2 expr2) ...) body-expr). let is nonrecursive, so that exprN can only refer to nameM for M < N. (You can reuse names, e.g. (let ((a 1) (a (+ 1 a))) a) gives 2.) letrec is recursive, so that any exprN can refer to any nameM. (I haven't implemented any checks to forbid you from reusing names here, but probably only the first or last use of a name would have any effect.)
Finally there's pattern binding with (if~ val pat if-match else). Pattern pat can be a literal string or float, or a variable name prefixed with $, or a constructor name possibly with other patterns as arguments. If the value matches the pattern, if-match gets evaluated, with any variables bound to the relevant parts of the pattern. Otherwise, else-match gets evaluated. For example:
(if~ 0 0 "zero" "nonzero") # "zero"
(if~ 1 0 "zero" "nonzero") # "nonzero"
(if~ (Just 3) Nothing "Nothing" "Just") # "Just"
(if~ (Just 3) (Just $x) x 0) # 3
(if~ Nothing (Just $x) x 0) # 3
(if~ (, 1 2) (, $a $b) (+ a b) (err! "impossible")) # 3
(I'm leaning towards # for comments when I get around to that. Also, I'm assuming here that the Maybe type has been defined.)
There's no equivalent of a case statement that matches the same thing against multiple patterns. For that you'd need nested if~, and there's no exhaustiveness checking (i.e. nothing that would say "you missed a possibility").
This is all typechecked, so that you get a compilation error if you try to multiply a string by a float or whatever.
You can add explicit type declarations to expressions, or to parts of patterns or to the variables in let or letrec bindings. A type declaration looks like (: expr type) and a type is either a bare name for a type constructor, or a $name for a type variable, or a type application like e.g. Maybe $a or -> (Maybe Float) String. The root of a type application has to be a constructor, not a variable.
(: 0 Float)
(: (λ x (+ x 1)) (-> Float Float))
(if~ (Just 3) (Just (: $x Float)) x 0)
(if~ (Just 3) (: (Just $x) (Maybe Float)) x 0)
(let (((: id (-> $a $a)) (λ x x))) (id 3))
If a type declaration is more specific than it could be, it constrains the type of the expression; if it's more general, that's an error:
(let (((: x (Maybe $a)) Nothing)) x) # valid, (Maybe $a) is the inferred type
(let (((: x (Maybe Float)) Nothing)) x) # valid, Float is more specific than $a
(let (((: x (Maybe Float)) (Just "foo"))) x) # not valid, Float /= String
(let (((: x (Maybe $a)) (Just "foo"))) x) # not valid, $a is more general than String
Apart from expressions, the statements I've implemented so far are def for global definitions, and type to declare a new type.
Currently all the def statements get pulled together and brought into a single letrec around the top-level expression. (Each program currently is required to have exactly one of those.) So
(def foo ...)
(foo bar)
(def bar ...)
is sugar for
(letrec ((foo ...)
(bar ...))
(foo bar))
Type declaration introduces new types, constructors, and eliminator functions. For example,
(type (Maybe $a) Nothing (Just $a))
introduces three values into the environment: Nothing of type Maybe $a; Just of type (-> $a (Maybe $a)); and elim-Maybe of type (-> $a (-> (-> $b $a) (-> (Maybe $b) $a))). This last is the standard Haskell maybe function, but you get one for free whenever you declare a type.
Other type declarations would look like:
(type Bool False True)
(type (List $a) Nil (Cons $a (List $a)))
(type (, $a $b) (, $a $b))
(type (Either $a $b) (Left $a) (Right $b))
(type Unit Unit)
(type (Proxy $a) Proxy)
(type Void)
(I'm tempted to name the standard unit type and its value ∅ instead. That's a bad name for the type, which is not an empty set, but it's a decent name for the value. It would be a fine name for the void type, but that type isn't useful enough to deserve such a concise name.)
letrec has something that's either a bug or, generously, a "missing feature that looks an awful lot like a bug when you don't realize that you're expecting it to be there". The way the typechecking works, inside the bindings for letrec, you can only use each bound variable at a single type. So you can't do
(letrec ((id (λ x
(let ((a (id 3))
(b (id "foo")))
x))))
...)
because that uses id at types -> Float Float and -> String String. (Never mind that if you could it would be an infinite loop.) Haskell has this limitation too, though I'm not sure I've ever run into it naturally; I couldn't think of a non-contrived example.
In Haskenthetical, this applies across an entire binding group. So you also can't do this:
(letrec ((id (λ x x)))
(some-float (id 3))
(some-str (id "foo")))
...)
But that example would work if you translated it to Haskell. What gives?
Well, since id doesn't depend on some-float or some-str, you could easily rewrite that example as
(letrec ((id (λ x x))))
(letrec ((some-float (id 3))
(some-str (id "foo")))
...))
And it turns out that Haskell just does that transformation for you automatically. It figures out what depends on what and groups them in such a way as to impose the fewest possible restrictions. If you make that impossible by adding some contrived mutual references, you can make Haskell fail in the same way:
let id_ x = const (const x someFloat) someStr
someFloat = id_ (3 :: Int)
someStr = id_ ("foo" :: String)
in ...
-- error: Couldn't match type ‘[Char]’ with ‘Int’
(You actually only need to reference one of someFloat or someStr, because once id_ is used at a specific type, it no longer generalizes to a -> a in the body of the let.)
I haven't implemented this in Haskenthetical yet.
Implementation
I don't think there's anything particularly exciting about the implementation, if you're familiar with such matters. But for those who aren't, and who want to hear about them from me, read on.
I parse¶ the input text into a list of syntax trees using Megaparsec. The syntax tree only knows about a few types of token:
data SyntaxTree
= STString Text
| STFloat Double
| STBare Text
| STTree [SyntaxTree]
Then I parse each tree into a statement (or expression, but that's just a type of statement) by recognizing specific STBare values (at the head of an STTree) as needing special handling and passing everything else through to "assume this is a function getting called".
Typechecking¶ is Hindley-Milner. When I wrote that essay, I said I didn't know how to implement HM typechecking. I have some idea now, and would describe it vaguely like this:
Recurse down the parse tree. At each step there are a few relevant types that you get to say "unify" with each other, roughly meaning "these are two different ways of writing the same type". Sometimes you look those types up in the environment, sometimes you just generate fresh type variables, and sometimes you generate fresh type variables and then add them to the environment. But as you go, you're building up a big list of constraints, pairs of types that unify. Also, each node gets a specific type assigned to it, which will generally be placed in a constraint. This stage is called "unification". For example, if you see the function call (foo bar), you'll recurse down to get types t1 for foo and t2 for bar, and you'll generate a fresh type variable t3 for the result. Then you'll say that t1 unifies with -> t2 t3.
When you've finished, you loop back over the list of constraints, and build up a substitution. Any time you see "this type variable should be the same as this other type", you add that to the substitution, and you make that substitution in the remaining constraints before looking at them. If you see two types that should be the same but the non-variable parts of them don't match up, that indicates a type error in the program. This stage is called "solving". For example, if we have the constraint that types -> $a String and -> (Maybe Float) String unify, then whenever we see type variable $a in future we can replace it with Maybe Float; if the second one had instead been -> (Maybe Float) Float, then those don't match up and the program doesn't typecheck.
In the end, you apply your substitution to the type of the program as a whole that you got from unification, and that's the ultimate type inferred for the program. If there are any type variables left, the program doesn't fix them. (An example of this would be if the program was simply Nothing.)
Of course it's more complicated than that. For example, let and letrec need you to run solving during the unification phase. Also, declared types need to be treated specially so that you can reject if the user declares Just 3 as Maybe $a.
Aside, a thing I don't fully understand: I haven't tried timing it, but this implementation looks to me like it's something like O(n²) in the size of the input. It's supposed to be roughly linear. I'm not sure if I'm missing something or if there's just a more efficient algorithm.
Anyway, that's roughly how I do it. I take this approach mostly from Write You a Haskell (notably chapter 7, section "constraint generation", but also other chapters were useful for other parts of Haskenthetical). But I had to figure out how to handle letrec myself, because the language implemented there uses fix instead. I also took a lot from Typing Haskell in Haskell, especially pattern matching. (I hadn't discovered it by the time I implemented letrec.) Neither source implements explicit type declarations, so I had to figure out those for myself too. I'm not convinced I did a very good job.
Finally, evaluation¶: for the most part that's fairly straightforward. For example, when we evaluate a variable, we look up its value in the environment. When we evaluate a let, we evaluate something, add it to the environment under the relevant name, and go on to the next thing. There are a few types of values¶ that we need only when evaluating:
- A closure is the thing that gets returned when we evaluate a
λ expression. It captures a snapshot of the current environment, the name of the argument, and the body expression. If a λ has multiple arguments, it returns nested closures.
- A builtin is a regular Haskell function of type
Val -> Either Text Val (plus a name to distinguish them). Builtins and closures are ultimately the only things that can be called as functions.
- A Thunk is an unevaluated expression, with a copy of its environment. They get evaluated as soon as anything returns them. Currently they're used in two places.
letrec needs them because we can't evaluate bindings before adding them to the environment or we'd get infinite recursion. Type eliminators are builtin values, but the Val they return is a Thunk (with empty environment) to avoid the Haskell file Env.hs from having to reference Eval.hs.
- A tag is just a symbol (a Haskell
Text under the hood) paired with a list of other values. Constructors wrap their arguments in a tag, and eliminators and pattern matching compare those symbols. There's no way to look at or manipulate the symbol directly in Haskenthetical, but I'd be curious to explore that direction.
I'll mention a couple other things that might be of note. These probably require more background knowledge of Haskell to make sense.
Firstly: I have the data type
data Pass = Parsed | Typechecked
type Ps = 'Parsed
type Tc = 'Typechecked
which some types use as a parameter, like
data TVar (p :: Pass) = TV !(XTV p) Name
type family XTV (p :: Pass)
type instance XTV Ps = NoExt -- data NoExt = NoExt
type instance XTV Tc = Kind -- the kind of a Haskenthetical type
This lets us use a slightly different type TVar in different parts of the codebase. When we've merely parsed the program, we have no way to tell the kind of a type variable, so we have NoExt there. When it's been typechecked, the kind is known, so we include it. If there was a pass in which type variables simply shouldn't exist, we could write
type instance XTV NoTVarPass = Void
and we wouldn't be able to use a TVar in that pass at all.
This technique is called "trees that grow", and I copied it directly from GHC. I'm not currently using it everywhere I could, for no principled reason that I can recall. There's a chance it'll be more trouble than it's worth at the level I'm working at. An annoying thing about it is that you can't use a regular deriving clause, so I have
deriving instance Eq (TVar Ps)
deriving instance Eq (TVar Tc)
deriving instance Show (TVar Ps)
deriving instance Show (TVar Tc)
deriving instance Ord (TVar Ps)
deriving instance Ord (TVar Tc)
which kind of sucks.
Secondly: builtin functions are kind of a pain to write manually. For example, either was previously defined as Builtin $ Builtin' "either" heither where
rbb :: Name -> (Val -> Either Text Val) -> Either Text Val
rbb name func = Right $ Builtin $ Builtin' name func
heither :: Val -> Either Text Val
heither l = rbb "either.1" $ \r -> rbb "either.2" $ \case
Tag "Left" [v] -> call l v
Tag "Right" [v] -> call r v
_ -> Left "final argument of either must be an Either"
(Builtin is a constructor of type Val containing a Builtin, and Builtin' is the only constructor of type Builtin. These names do not spark joy.)
It works, but it always felt like I should be able to do better. I spent a while trying to figure that out and now the value is simply heither where
heither :: Val
heither = mkBuiltinUnsafe $ do
l <- getArg "either"
r <- getArg "either.1"
e <- getArg "either.2"
pure $ case e of
Tag "Left" [v] -> call l v
Tag "Right" [v] -> call r v
_ -> Left "final argument of either must be an Either"
I dunno if this is much better, honestly, but there we are. It needs ApplicativeDo; I never managed to either figure out a Monad that could do this, or prove that no such monad exists. (There's no Monad instance for the specific type that I use to implement this, because to write join for that monad you'd need to be able to extract the inner [w] from ([w], r -> ([w], r -> a)) without having an r to pass to the outer function, and that's not a thing that even makes sense to be able to do. But there might be a different type that enables what I'm trying to do and does admit a Monad instance.)
So that's where it's at right now. Feel free to point out ways that it sucks, although not-sucking isn't the point. I'm also interested in pointers to how I might implement some of the things on my future list (I'm aware of Implementing a JIT Compiled Language with Haskell and LLVM), or other cool things I may like to put on that list, or even things you might happen to like about Haskenthetical.
Posted on 19 May 2020
|
Comments
Update (May 8th 2020): Some small updates to the interferon and vitamin D sections.
Update (29th April 2020): I've made a significant update to the vitamin D section in response to version 3 of the report.
Background on this in part one.
General info: Interferon
Interferon is an antiviral that our immune system naturally releases when it detects invasion. But SARS-CoV and MERS-CoV (the virus that causes MERS) manage to avoid this response. The trigger is the presence of double-stranded RNA, which viruses need but our own cells don't. (We make single-stranded RNA from DNA, and then proteins from single-stranded RNA. We never need to copy our RNA. But viruses do need to copy their RNA, and apparently that means viral RNA needs to be double-stranded.) SARS-CoV and MERS-CoV hide their double-stranded RNA inside "double-membrane vesicles" to avoid detection.
Update May 8th 2020: I've seen multiple sources saying SARS-CoV-2 is a single-stranded RNA virus, and wikipedia says SARS-CoV and MERS-CoV are too. I'm a bit confused by this, and frustratingly Chris doesn't cite this part. From a quick google, the abstract of this paper sounds like a single-stranded RNA virus can still have double-stranded RNA, or produce double-stranded RNA at some point, or something? Note that Chris doesn't say that the viruses are double-stranded RNA viruses, just that they have double-stranded RNA.
They also have a bunch of other ways to limit production of interferon, and on top of that they limit the response to the interferon that does get produced.
This all sounds like "so we should ramp up interferon". But that's probably a bad idea. During early stages of the virus, interferon is suppressed, so the virus can replicate quickly. But when the infection is established, macrophages generate a lot of interferon, leading to a cytokine storm. In a mouse trial, deleting the genes for the main interferon receptor made the subjects very resistant to SARS-CoV, but very vulnerable to mouse hepatitis virus and influeza A, compared to normal mice. (0% died to a dose of SARS-CoV that killed 85% of normal mice; but 100% died to a dose of the other viruses that killed 10-20% of normal mice.)
(Question: "During the replication of the virus, macrophages are recruited to the lung". These are what release the interferon. What is a macrophage and what is recruiting them and why?)
We don't yet know that any of this applies to SARS-CoV-2 as well, but it seems likely. So high levels of interferon might be slightly helpful in early stages, but make later stages much worse. Thus, Chris recommends avoiding them.
(Question: LW user CellBioGuy is bullish on inhaled interferon pretreatment, which I take it means "inhaling interferon before the disease gets bad". Does this square with Chris' recommendations? It wouldn't surprise me if inhaling interferon increases your levels in the short term but not the long term, which is exactly what we want. On the other hand, he links a paper whose abstract says SARS-CoV-2 "is much more sensitive [than SARS-CoV] to type I interferon pretreatment", so maybe this is just a case of "generalizing from SARS-CoV didn't work here".)
On April 25, Chris wrote more about this on his mailing list. My own summary: in hamsters infected with SARS-CoV-2, eliminating the type 1 interferon response increased the amount of virus in various body parts including the lungs; but dramatically reduced lung damage. Chris notes that this is a bit weird, but takes it as supporting his hypothesis, and I'm inclined to agree.
Every-day optional add-on: Garlic or stabilized allicin
Allicin is the thing we care about here, garlic is just one way to get it. Garlic doesn't actually contain any, though. Garlic contains alliin. Alliin is converted to allicin when the garlic is crushed and left at room temperature in the open air for ten minutes.
(Who decided to name those things with an edit distance of one, and how do we stop them from naming anything ever again?)
Alternatively, we can mix garlic powder with water, and let that sit at room temperature in the open air for ten minutes. That gives us a more reliable dose, since garlic cloves vary in size. Or we can just take stabilized allicin supplements, which is a still more reliable dose. Most garlic extract won't work, and "potential allicin" is unreliable. Meals containing garlic won't work, because allicin isn't robust to heat or acids.
180mg allicin daily makes people less likely to get colds. (I note that Chris here seems more confident than the authors of that review, who only found one study matching their inclusion criteria and who say at different times that the evidence is "poor-quality" and "moderate". Looking at the excluded studies, two seem worth noting. Both were excluded because they grouped colds and influenza together. Andrianova 2003 found that a specific brand of garlic tablets "allicor" reduced morbidity from acute respiratory diseases 1.7-fold. So that seems to support Chris' recommendation. Nantz 2012 used aged garlic extract, and found that it didn't reduce the incidence of (colds + flu) but did reduce the number and severity of symptoms. It's not clear to me whether aged garlic extract even contains allicin, but these results seem a little confusing to me whether it does or not.)
We also see antiviral effects in vitro against six different viruses: "herpes simples virus type 1, herpes simplex virus type 2, parainfluenza virus type 3, vaccinia virus, vesicular stomatitis virus, and human rhinovirus type 2". It seems to work by damaging the lipid envelope of those viruses. So it might also work against coronaviruses, which also have a lipid envelope.
Separately, allicin has antibacterial effects, which work by the same mechanism as zinc and copper inhibit SARS-CoV enzymes, so maybe it also inhibits those enzymes. (Note, this is not the same mechanism as how copper surfaces destroy SARS-CoV.) And it inhibits papain, so maybe it also inhibits papain-like proteases. (It sounds like papain-like protease 2 could be targeted by both these effects, and there are other papain-like proteases that could only get targeted by the second?)
Chris recommends this as an optional daily add-on, because although it's never been tested directly against coronaviruses, it's plausible and seems to be safe.
If you get sick, optional add-on: Echinacea
I've never heard of this. Apparently it's a herb. It "has been used for the common cold", which isn't saying much (what hasn't?) but the citation suggests it was also at least somewhat effective. But this seems to be the only evidence Chris provides that it has any positive effects at all; Wikipedia is skeptical.
The mechanism of its effect seems to be boosting the immune system, so we might worry that it does so by increasing interferon. But instead it seems to work by increasing "inducible nitric oxide synthase" (iNOS). That doesn't seem to be protective against contracting SARS, but in mice it helps protect against the long-term damage that SARS does to the lungs.
Chris thinks this is less important than all of the preceding compounds, because "there is no clear evidence echinacea will offer specific protection against COVID-19". He no longer thinks it's safe long-term (though he hasn't updated the in-depth section of his report to reflect that), so he recommends only taking it when you get sick.
Everyday optional add-on: Vitamin C
Vitamin C supplements seem to prevent colds, but not necessarily cure them. Intravenous vitamin C reduced mortality of acute respiratory distress syndrome by half; but none of those patients had SARS. Studies have shown conflicting effects of vitamin C on interferon levels, variously increasing and decreasing it.
Chris recommends getting enough vitamin C "to support normal immune function", which means taking supplements if and only if you don't get enough from your diet. He thinks the chance of it increasing interferon is too risky to take high doses.
No longer recommended? N-Acetyl-Cysteine
In the first version of the report, Chris considered this an optional add-on. He no longer includes it in his list of recommendations, but the sections where he explained his recommendation are still in the report, unchanged. I'm not sure what's up with that.
Another thing that I'm not sure what's up with. In one section, Chris says: Normally we get cysteine by eating protein. NAC helps us get more cysteine into our cells, and the extra cysteine is good for the immune system and lung health. In another section, he says NAC "is a precursor to glutathione, which is critical for lung function." He's not very detailed about either of these claims, so I'm not sure how to put them together, and a quick glance at wikipedia doesn't really help. (There's totally room in my lack-of-understanding for them both to be true, it's just a bit weird that we have two different descriptions of its effects.)
Apart from being generally good for the lungs, the reason for recommending it - if he does recommend it - seems to be a single case where large amounts of NAC helped someone to recover from pneumonia caused by H1N1. There's no reason to think it might help prevent COVID-19, but it might help mitigate the damage.
Limit: Vitamin A
Vitamin A is vital to the immune system, and you shouldn't get deficient. But its active metabolite is all-trans retinoic acid. In many rat studies, that's increased ACE2: "in the heart of rats whose blood pressure was raised by constricting their aortas, in the heart and kidney of spontaneously hypertensive rats, in the kidney of rats with glomerular sclerosis (to much higher levels than even healthy control rats), and in rat tubular epithelial cells subject to hypoxia-repurfusion." Since that effect seems fairly consistent, there's a significant risk that increased levels of vitamin A would increase levels of ACE2, which (as discussed in part 1) seems likely bad. So Chris recommends getting only enough vitamin A to avoid deficiency.
(Question: how easy is it to avoid publication bias / confirmation bias / etc. here? If some people found situations where ACE2 didn't get raised by Vitamin A, would that result have been published and would Chris have found it? He does mention studies like that for vitamin D, so that's at least evidence for yes and yes.)
Supplement to a point: Vitamin D
Like vitamin A, vitamin D runs the risk of increasing ACE2 levels. We have three rat studies supporting this, two rat studies contradicting it, and one human study contradicting it.
The supporting rat studies show that: "Calcitriol, the active metabolite of vitamin D, increases ACE2 mRNA and protein in rat pulmonary microvascular endothelial cells treated with lipopolysaccharide, synergizes with diabetes to increase ACE2 protein in the renal tubules of rats, and in the brains of both hypertensive and healthy rats."
Of the contradicting evidence, the human study and one of the rat studies looked at serum ACE2, i.e. ACE2 which has been shed from cells and is circulating (I guess in the bloodstream). Serum ACE2 won't help the virus gain entry to cells, and might help protect against it. (No citation or explanation for this, but I guess the reasoning is that if the relevant part of the virus binds to serum ACE2, it won't subsequently be able to bind to ACE2 on the cell wall.) Serum ACE2 might not correlate with docked ACE2. Additionally, the rat study showed that vitamin D depletion had no effect on serum ACE2, but that doesn't mean an abundance of vitamin D would also have no effect; and the human study only showed a statistically significant difference in people with stage 5 kidney disease (with less severe kidney disease, the difference wasn't statistically significant; in healthy controls there was no difference).
The final rat study was looking at injury response of rat kidneys; the injury in question would normally increase ACE2 levels but vitamin D (or at least calcidiol, its partially activated metabolite) reduces that effect. But this seems to be caused by vitamin D making the kidneys more resilient to injury, not by directly suppressing ACE2. So it probably isn't relevant here.
Weighing up, vitimin D seems likely to increase ACE2, and in versions one and two of the report Chris recommended against supplementing it (but still against becoming deficient).
Update (April 29th 2020): The rest of this section is based on info added in version three of the report, which Chris released less than an hour after I published.
However, vitamin D may affect some of the factors that predict a severe or lethal case of COVID-19. The factors Chris mentions are: "low lymphocytes, a high ratio of neutrophils to CD8+ T cells, and high interleukin-6 (IL-6)." (These are all in the bad direction, i.e. low lymphocytes predicts worse disease progression.)
There's lots of confusing and somewhat contradictory studies here. Some of it is to do with CD4 T cell counts, which I'm not sure what the relevance is. But it seems there's at least some reason to think that vitamin D supplementation may sometimes increase lymphocyte counts and/or decrease the ratio of neutrophils to lymphocytes. (I guess that last is good for at least one of those factors whether it incseases the numerator or denominator, as long as it doesn't decrease CD8+ T cells.)
There's also lots of studies on the effect of vitamin D on IL-6 in specific contexts. "Middle-age and older adults": four studies, no effect. "Hemodialysis patents": four studies, no effect. "Obese and overweight patients": eight studies, no effect. "Diabetes": five studies, no effect. "Heart failure": reduction in one study, not in another. "Diabetic kidney disease": three studies, reduction in all. "Ventilator-associated pneumonia": one study, reduction. Notably, this last is most relevant to COVID-19.
Chris sums up: "A reasonable interpretation of these studies is that vitamin D does not affect IL-6 under conditions of chronic low-grade inflammation, but does lower IL-6 during acute and highly inflammatory conditions." (I note two reasons to be unsure of this. Firstly, that with this many conditions being tested, and so few positives, we should probably make sure we're not accidentally p-hacking. Secondly, that the the pneumonia study involved "intramuscular injection of 300,000 IU vitamin D" which may not tell us much about oral vitamin D supplements of less than 1% that amount.)
But we also have observational studies between vitamin D levels and COVID-19 severity. Chris has written about one of them publicly; the other is here, though I think all the specific numbers in the report are from the first one. The summary is that given a case of COVID-19, case severity is strongly correlated with low levels of vitamin D in the bloodstream.
We haven't established causality here, and there's reason to think it goes the other way (inflammation depletes vitamin D).
We have no information on high levels, and Chris is worried about a U-shaped curve. I note a complexity penalty: if the correlation is monotonic in the region of the space that we've explored, expecting it to shift direction in the space we haven't explored requires some justification. Is there a reason it doesn't shift in the space we explored, or just bad luck?
Chris doesn't really address this. But the space we haven't explored here is [anything above the level associated with the lowest all-cause mortality] ("in all relevant studies except a single outlier that was only published as a conference abstract"). Plus, if we assume the patients mostly weren't supplementing vitamin D, then maybe the space we haven't explored here is also [anything above the highest natural levels humans seem to reach], and it's not too surprising if things shift direction in that space. So it's not as suspicious as it looks at first.
Anyway. Based on all this, Chris now recommends aiming for a specific level of vitamin D in the bloodstream: 30 ng/mL. He thinks the ideal is to test your levels every 2-4 weeks, but the home testing kit he links to seems to cost $65/test plus shipping, and he hasn't convinced me it's worth that much. Failing that, he recommends supplementing 1000 IU/day.
(I also note that, by recommending against both supplementation and deficiency, Chris was always implicitly predicting a U-shaped curve - just with the inflection point at a lower level. By comparison, different institutions generally recommend daily intakes around 600 IU/day. So supplementing 1000 IU, on top of whatever you get from food and sunlight, seems like give-or-take doubling his previous recommendation.)
Update May 8th 2020: Chris has now also written about the second study as well as two others that don't change his recommendation. We now have a little data about patients with high vitamin D levels - not enough to draw strong conclusions, but at least one of them did have a severe case. He says these studies make the link between vitamin D and severity seem to be more robust but weaker - that is, he's more confident that there is a link, but the link seems less strong than previously.
Limit: Calcium
And balance it with phosphorus. There's a complex system keeping them balanced in the blood, and they often have opposite effects. Notably, a high calcium:phosphorus ratio suppresses fibroblast growth factor 23, and a low calcium:phosphorus ratio increases it. FGF23 suppresses ACE2, so a high calcium:phosphorus ratio might increase ACE2. Chris recommends limiting calcium supplements to 1000 mg/day, and matching supplemental calcium with supplemental phosphorus 1:1.
Avoid: Pelargonium Sidoides
This is also called Umcka. I don't think I've previously heard of it under either name. It has many of the same components as elderberry, but only a small amount of caffeic acid. Caffeic acid was what gave us most reason to think elderberry would work, so Umcka seems inferior to elderberry.
Umcka does have some antiviral effects, including against HCoV-229E, but the mechanism for that is unclear. In cell cultures it increaes iNOS like echinacea; but also interferon, so if that generalizes it would be risky to take. It also increases neutrophil activity; those are part of the immune system, so naively we might think that was a good thing, but high neutrophil counts seem to make SARS worse.
So basically this seems like it offers nothing we can't get from elderberry and echinacea, and is too risky. So Chris recommends avoiding it.
Avoid: Honeybee Propolis
This hasn't been found to have significant direct antiviral properties against any viruses. It increases interferon responses in mice and chickens, so it may be somewhat helpful against some viruses, but it's too risky to use here. Chris recommends avoiding it.
Avoid: Monolaurin
Monolaurin seems to damage lipid envelopes, as well as the membrane of cells without cell walls, so SARS-CoV-2 is probably vulnerable to it. But so are human T cells. The risk of impairing those seems unacceptably high, and Chris recommends avoiding monolaurin.
There's an argument that it hurts only pathogens "because it is effective against yeast and the bacteria that cause bacterial vaginosis, but not against lactobacillus", but Chris thinks that's just because lactobacillus has a cell wall, and there are probiotics which don't have anything like that which would probably be vulnerable too.
(I think the idea that this would only hurt pathogens seems absurd, but what do I know. The citation for that clause doesn't seem to present the argument, so I'm not sure who's making it or if Chris is representing it accurately, but people have been to occasionally say absurd things.)
Posted on 28 April 2020
|
Comments
If you maintain an open source project, what responsibilities do you have towards your users? Some recent drama (that I won't link to) reminded me that there are large differences in how people answer that question.
(In the drama in question, this wasn't the only thing at issue. But it was a relevant question.)
I thought I'd take a stab at describing my best guess as to how we answer it in my culture: in the culture that exists only in my mind, but that I think (and hope) many copies of me would implement, if we had that opportunity. (That culture doesn't attempt to exclude people who aren't copies of me, so it does need to be robust to attack. In my culture, we do not just assume in defiance of all evidence that everyone is friendly and trustworthy.)
Some of this will probably seem obvious to many readers, like "in my culture, murder is considered bad". Probably different bits to different readers. I'm interested in discovering which bits seem obvious to almost everyone, and which bits are controversial.
A lot of it follows from how I think about responsibility in general. But if you start to think "extending this response to this other situation, you'd get this, and that's a terrible idea"… in my culture, we don't immediately assume from this that I'm endorsing a terrible idea. Instead we check. Maybe I disagree that that's how it extends. Maybe I hadn't thought about this, and you can change my mind about the initial response. Maybe I just straightforwardly endorse a terrible idea: in that case, it'll be much easier to push back once you've gotten me to admit to it.
I do not intend, in this essay, to discuss whether any particular person or group is living up to the standards I outline here. I may do that in future. But how likely that is, and what that follow-up looks like, depends on whether the responses to this essay suggest a lot of people agree with my culture.
I think there are at least three important limitations to this essay. One is that I've never been a maintainer of an open source project that had users other than myself (that I knew of), though I've made small contributions to a few. As such, I don't really know what the experience is like or how my culture deals with its challenges, much like I don't really know how my culture deals with the challenges of living in Antarctica. I can make educated guesses, but that's all they are. I'm not going to explicitly flag them as such in the main body. (I'm already using the words "in my culture, we…" far too much. I'm not changing it to "in my culture, my educated guess is that we…") Ideally, I wouldn't write this essay because there was already a conversation taking place between people who knew what they were talking about. Unfortunately, as far as I've seen there mostly isn't, so I offer what I can.
Another is that I don't talk at all about the responsibilities of users, which is also an important part of the question. I'd like to, but… this essay has been knocking around in my head for at least a year and a half, I've made at least one previous attempt to write it that I gave up on, and I'm worried that if I don't publish it quickly I never will. I hope and believe that even with this omission, it is better for this essay to be published than to not be published.
(I also omit the question "what is this responsibility thing anyway?", but that seems less important to me right now. I've probably also overlooked important parts of the things I do talk about, but that too may not be a big deal.)
And a third is that without specific examples, what I've written is less constrained than what's in my head. It may well be possible to read this and agree with what I've written, and then to discover that your culture has a much stricter or much looser conception of responsibility than mine does.
With all of that out of the way: there are three questions I'm going to be focusing on here. When is responsibility taken on; what does it entail; and how do we react if people fail at it?
When is responsibility taken on?
In my culture, taking on responsibility requires active involvement, but not explicit consent. It's possible to take on responsibility through negligence - to draw responsibility towards yourself without realizing that's what you're doing. In my culture, we're sympathetic towards people who do that, but we don't consider that this absolves their responsibility.
In my culture, merely making something available does not make you responsible for it. If you want to put something online and ignore anyone who tries to use it, you can do that. You are allowed to shithub.
In my culture, you take on more responsibility for a project if…
-
If you start encouraging people to use your project. If someone happens to stumble across a repository you never specifically shared, you have no responsibility for it. If you see them describe a problem they have, and you say "oh hey, I had that problem too, you might want to check out my repo" you have a little. If you create a website for your project where you describe it as "the best way to solve this problem", you have more.
-
If you have many users. If you shirk your responsibilities, most of the harm done is to your users. With fewer users, the harm from not-acting-responsibly is lower, and so the responsibilities themselves are lower.
-
If your users are invested in your project. If they can't easily stop using it, you have more responsibility to treat them well.
Your users' exit costs are probably low if you make a video game, or "libpng but 30% faster" or "find but with a nicer command line syntax". In that case your users can probably just play a different game, or easily replace your tool with libpng or find.
They're higher if you make a programming language, where migrating away requires rewriting a codebase. Or a document editor that can only save in its native binary format or pdf, so that there's no way to edit the documents without your tool.
-
If you have the ability to accept responsibility. Handling responsibility takes time and it takes multiple skill sets. One person hacking on their side project simply cannot act in the same ways as a team of two full-time developers plus twenty volunteers. That team can't act in the same ways as the Mozilla Foundation.
-
If you act like you're accepting responsibility. If you have a history of ignoring issues and pull requests, people should probably pick up on this. If you tell people you're going to break backwards compatibility, they shouldn't expect you to maintain it. Words like "production ready" increase your level of responsibility. Words like "alpha" decrease it, as do version numbers below 1.0.
A common thread here is that responsibility is related to justified expectations. "Expectations" in both the moral sense and the probabilistic sense. If someone can make a compelling argument "this person morally ought to accept responsibility here", or a compelling argument "I predict based on past behaviour that this person will act as though they've accepted responsibility here", then in my culture, that person has some degree of responsibility whether they like it or not.
Accordingly, in my culture you can disclaim responsibility in advance, simply by saying that you're doing this. Note that a pro forma warranty disclaimer in your LICENSE file isn't sufficient here. Instead you should say it at the entry points to your project - probably the README and the website (if there is one). Something like…
Note that while I think this project will be useful to many people, I am not devoting much attention to it, and I'm prioritizing my own use cases. Bugs may be fixed slowly if at all. Features may be removed without warning. If this isn't acceptable to you, you should probably not rely on the project; or at least you should be willing to fork it, if necessary.
Or even:
Note that while I think this project will be useful to many people, I have no interest in accepting responsibility for other people's use of it. Feel free to submit issues and pull requests; but I may ignore them at whim, and my whim may be arbitrary and capricious.
This won't usually be necessary. But if you feel in danger of taking on more responsibility than you'd like, you can do this.
If you have responsibility, what does that entail?
In my culture, if we've taken on responsibility and now we want to discharge it, we do so with care. We give advance notice, and we try to find replacement maintainers. If we can't find a replacement maintainer, we still get to quit. But we try.
In my culture, we acknowledge that different people have different needs and goals, and not every project will be suitable for all users. We try to help users figure out whether our projects will be suitable for them before they get invested. We're open about the limitations of our projects, and about the design goals that we explicitly reject.
In my culture, we don't need to reply to every critic. But we do try to notice common threads in criticism, and address those threads. ("Address" doesn't mean that we necessarily try to solve them in a way that will satisfy the critics. It simply means we give our thoughts about them. We try to do that in such a way that even if the critics aren't happy with what we're doing, they at least feel like we've heard them and understood them.)
In my culture, we accept that some critics will be unkind, unfair and unproductive. This sucks, but it's a reality of life right now. We distinguish these critics from others. We are free to ignore them, and to ban them and delete their posts from the spaces we control. We do not use their actions to justify shirking our responsibilities to other critics.
In my culture, we also take care to check whether we're unfairly rounding people off as being unkind, unfair and unproductive. We don't require perfection from our critics. We try to hold ourselves and our supporters to the standards we expect of our critics. We moderate our spaces, but we try not to silence all criticism from them.
In my culture, we still introduce bugs, because we're still human. We try not to, of course. But we accept fallibility. When we fail, we do our best to fix it. We put more effort into avoiding more catastrophic bugs.
In my culture, we do not accept incompetence or indifference. These are signs that a person should not have taken on responsibility in the first place. We expect people to know the limits of their ability and of how much they care.
In my culture, we can set boundaries around how our future actions are constrained. We distinguish public APIs (where we mostly try to maintain backwards compatibility) from private APIs (where we mostly don't, and if people expect us to we point to the word "private"). We may reject bugfixes that we expect to cause too much ongoing future work, in hope of finding a better fix in future.
In my culture, sometimes we hurt people deliberately because the alternatives are worse. When we do, we own it. For example, sometimes we decide to remove a feature that people were relying on. We don't make that decision lightly. When we do it, we explain why we decided to do it, and we apologize to the people who were relying on it. We don't try to minimize their pain. We try to suggest alternatives, if we can; but we try not to pretend that those alternatives are any more suitable than they actually are. We give advance notice, if we can. We can be convinced to change our minds, if new information comes to light.
Of course, the degree to which we feel bound by all of this depends on the degree to which we've actually taken on responsibility. And note that in all of this, there's very little requirement for positive action. If we don't want to include a feature, we don't need to write it, or even merge the PR if someone else writes it. If we don't want to go in the direction our users want us to, we don't have to go there. We just have to make it clear that that's what we're doing.
What if someone fails to act responsibly?
That is, if someone has taken on responsibility, whether intentionally or not, and then has failed to act like someone who's taken on responsibility… how do we respond?
In my culture, we mostly respond by acting as though this will happen in future.
We don't treat this as an indelible black mark against all aspects of the person. We'll still accept their contributions to other open source projects, for example. (Though perhaps not technically complex contributions, that will likely need a lot of maintenance from the same person going forward.) We'll accept their conference talks. We'll stay friends with them.
But we won't rely on their projects, because we don't expect their projects to be reliable. We warn others about this, but if others decide to use their projects anyway, we consider that none of our business.
We accept that people have a right to run projects as they see fit. We acknowledge that our conception of "responsibility" is a mere social convention. But social conventions are important. We provide an opt-out for this particular social convention, but if you don't opt out explicitly, we'll make it explicit for you.
We give second chances. If they want to take on responsibility in future, and if they seem to understand how they failed in the past, and they say they'll try to do better, we give them a shot, because that's reason to think it won't happen in future. If they still fail, and want a third chance, we take their second failure into account too.
We may fork a project, even if the maintainer doesn't approve, but we'll rarely attempt a hostile takeover from the outside. We'll make sure our fork is clearly distinguished from the original project.
Posted on 13 April 2020
|
Comments
Update (April 28th 2020): Part 2 published. Also a minor update to the ACE2 section.
Update (April 5th 2020): Chris released version two of his recommendations on April 2nd. There are some fairly major revisions. In particular, Chris now thinks Coronavirus infects the throat, not just the lungs. He was already making recommendations just in case this turned out to be true, so he hasn't specifically added anything, but it's still an important update. The other thing of note is that he no longer recommends using copper spray or taking echinacea until you get sick, except (for the copper) before and after potential exposure. I've updated this post accordingly. You can still read version 1.
Chris Masterjohn is a nutritionist who has some advice on supplements to take to help protect against Covid-19, and some to avoid. The raw advice is available for free, but the full report with explanation and references costs $10. I bought a copy. (The public advice has not been updated to reflect version 2.)
Should we trust him? On the one hand, "nutritionist" is not a profession I necessarily hold much respect for (it's not a protected term). Nor do I tend to think highly of people emphasizing that they have a PhD. Also, his website looks super sketchy to my eyes. Also also, something that costs money gets fewer eyeballs than something free, and so mistakes are less likely to be discovered.
(Only the last one of those should be considered a problem with the report; the rest are just priors.)
On the other hand, Chris previously turned me on to zinc so he has some credibility with me. Also, although I'm out of my depth in actually evaluating the science, I do think I have a decent bullshit detector, and the report is superficially very convincing to me. I get the sense that he actually really knows what he's doing, is weighing the evidence appropriately and making claims that are justified by it. He admits to uncertainty, and some of his recommendations are "this probably won't help, but just in case"; but he does speak precisely enough to be falsifiable. This doesn't mean he's right, of course. But I think he's worth some people paying some attention to.
My intention here is mostly to summarize his reasoning, in more detail than is on the linked page but less detail than is in the full report. You can make up your own minds. Much of it I haven't even checked how actionable it is right now (i.e. are these things available in stores or for delivery, and how much do they cost). I do have some questions and commentary of my own that I've scattered about, possibly not always well-flagged.
The report makes fifteen recommendations about fifteen supplements (some supplements are in multiple recommendations, and some recommendations are about multiple supplements):
- Four everyday "essentials": elderberry, nutritional zinc, ionic zinc, and copper.
- Two everyday "potential add-ons": garlic or stabilized allicin, and vitamin C. Chris takes allicin, and plans to take a low-dose supplement of vitamin C if he runs out of fresh food.
- Two things to use before and after every potential exposure: copper spray, and more ionic zinc.
- Two additional "essentials" only when you get sick: again, copper spray and more ionic zinc.
- One "optional add-on" only when you get sick: echinacea. Chris used to take this daily, but has since decided against that.
- Four "things to limit or avoid": these are much less pithy. "Don't take high doses of vitamins A or D" (but don't get deficient either); "Limit Calcium and Don't Use Calcium Supplements That Aren't Balanced by Phosphorus"; "Don't Use Monolaurin"; "Don't Use High-Dose Vitamin C, Pelargonium Sidoides (Umcka), or Bee Propolis".
"Potential exposure" is quite broad, including:
- Going into public spaces to perform essential errands.
- Accidentally encountering someone you don’t live with face-to-face within six feet, or making physical content with such a person.
- Touching any surfaces that someone you don’t live with may have touched in the last nine days without any personal protective equipment.
- Incorrect use of personal protective equipment (for example, taking gloves off your hands in any other way than explained here or reusing a mask without following these guidelines).
- Putting your fingers into your mouth or nose, regardless of whether you washed them beforehand.
I think he's mostly expecting these won't happen very often. Personally, I'm doing most of them about once a week to go shopping, and the last one probably several times a day.
It includes any physical contact with someone you don't live with, coming face-to-face with such a person within six feet, and putting your fingers in your mouth or nose even if you washed them first.
In this post I'm going to focus on elderberry, zinc and copper; my current plan is to do the rest in future posts.
So far, I've followed this advice to the extent of:
- I've stopped taking daily vitamin D supplements, and advised my partner to do the same. (Somewhat to my embarassment, as they'd only started taking them on my recommendation. I've been taking it 5x/week for years.) He says not to supplement with vitamin D at all, but he also says to get normal amounts from sunshine and vitamin D-rich foods, and we're not doing that. So maybe we should take one a week instead of one a day.
- I bought a bulb of garlic, but I haven't done anything with it yet.
- I took one of the zinc capsules that came free with my last order of zinc lozenges. Then I had a bad gastrointesinal day. Possibly unrelated, but they also had something of an unpleasant smell that I don't know whether it was normal. I haven't tried again. Maybe I will. They're 50mg, which is more than Chris recommends at one time.
- I recently started developing cold symptoms, so I would have been taking ionic zinc anyway. But I've probably taken more than I would have done otherwise. (I'm down to about 40 lozenges and they're currently out of stock, so I may not use them daily.)
If you're going to follow any of it yourself, you should at least read his public post, and ideally also the full report.
General info: ACE2
SARS-CoV-2 (the virus that causes the disease Covid-19) is not like the common cold or the flu, and things which work against those may not be helpful here. On the other hand, it's very like SARS-CoV (the virus that causes SARS). The genomes are 80% identical, and "the majority of its proteins are 85-100% homologous, with an average homology of 87%".
(Question: That seems like a really low average, given that range? Though I guess it includes the ones below 85%.)
The two main things the report focuses on are ACE2 and interferon.
ACE2 is an enzyme used in regulating blood pressure. SARS-CoV-2 enters our cells by docking to ACE2. It has this in common with just two other human coronaviruses, SARS-CoV and HCoV-NL63. So heightened levels of ACE2 could increase susceptibility to SARS-CoV-2.
(Question: "The binding of SARS-CoV to ACE2 is thought to downregulate ACE2 expression, leading to a loss of the anti-proliferative and anti-fibrotic actions of ACE2 in the lung, thereby contributing to the lung damage that occurs in SARS." That seems to point in favor of increasing levels of ACE2, so that it getting downregulated is not such a big deal. How to weigh these two concerns? I haven't read it closely, but this sounds like NL63 only affects ACE2 on infected cells, and doesn't so much "downregulate" it as "obliterate" it. So my super tentative take is: even if we start with high levels, that may not be sufficient to be protective if the infection gets bad; it would be more important to focus on stopping it from getting bad. But followup questions would be: what percent of cells express ACE2? What percent of those get infected, in a (light/moderate/bad) infection? When we do things that increase/decrease ACE2, does that increase the amount of ACE2 on individual cells, or the number of cells with any ACE2, or both? If a cell has lots of ACE2, does it do more of the sorts of things that ACE2 is good for?)
Update 28th April 2020: Chris has written more about this, see section "ACE2: Friend or Foe?" He points out that differing ACE2 levels are likely to have much more effect on viral replication (which is an exponential process) than on normal bodily functioning (which isn't).
I'll talk about interferon in a future post, because it's not relevant to anything in this post.
Daily essential: Elderberry
"In rhesus monkey kidney cell culture, elderberry has virucidal, anti-plaque, anti-replication and anti-attachment activity toward HCoV-NL63". Most of the effect seems to come from caffeic acid. That binds directly to ACE2, which suggests elderberry would be similarly effective against SARS-CoV and SARS-CoV-2.
(Question: is that in vitro? Doesn't seem very reliable in general, but maybe the specific mechanism makes it moreso.)
As a bonus, elderberry is also effective against avian infectious bronchitis virus through compromising the lipid envelope. Since all coronaviruses have one of those, that effect might generalize to SARS-CoV-2.
Other foods include caffeic acid, but only black chokeberries have anything like a comparable amount. And elderberry extract is the thing that's been actually studied, so that's what Chris recommends.
There are studies using elderberry in humans to treats colds, the flu, and cardiovascular disease, but Chris doesn't mention their results. He just uses them to determine a safe dose.
Daily essential: Nutritional zinc
This is zinc from food or most supplements (including tablets or capsules).
Zinc "inhibits at least two proteins required for SARS-CoV replication, papain-like protease-2 and helicase." So it probably inhibits the homologous proteins in SARS-CoV-2. (In version 1 Chris thought it also inhibited the protein helicase, but he no longer believes that.)
(Question: how similar do proteins need to be for this to be a decent guess? This suggests proteins called "homologous" might be only 40% similar in sequence. If I guess that "homologous" means this is likely to be a decent guess; and that these ones are >85% similar (based on base rates of similarity between the viruses)… that suggests it's probably a pretty good guess? But I'm not at all cofident in this thinking.)
So we should try to deliver zinc to the relevant tissues. What are those?
The infection would begin somewhere between the nose or throat (where the virus mostly enters our body) and lungs (where it primarily infects), wherever the virus first encounters ACE2.
(Question: this seems to assume that the virus doesn't first infect something outside of this path, and then move on to the lungs. Is that a safe assumption? I would guess so.)
In version one, Chris thought the virus wouldn't find any ACE2 until it reached the lungs. To quote the previous version of this post:
There are two papers trying to answer this question, and they give different opinions. …
Hamming et al (2004) suggests that the virus wouldn't find any ACE2 until it reached the lungs. They did find ACE2 in the oral and nasal mucous membranes, but on the wrong side to be any use to the virus.
Xu et al (2020) argues that ACE2 is highly expressed through the surface of the mouth, especially the tongue.
The two used different methods. Xu had better resolution, down to single-cell. But Hamming could tell where on the cells the ACE2 was expressed. The second thing matters, and the first doesn't. Xu's results are what Hamming would have predicted, they just aren't relevant. (The symptoms are also what Hamming would predict: a cough suggests lung infection, and is present. A runny nose or other cold symptoms would suggest throat infection, but they aren't present.)
But now there's direct evidence that the virus infects the throat too. (Note that the "not-yet peer reviewed" paper is now peer reviewed.)
So it seems that although the main infection site is the lungs, the infection starts in the mouth, nose or throat. We can specifically target those with ionic zinc, for which see below.
We don't have a specific mechanism to target the lungs with zinc. We just have to take it orally in the normal way (that is, in food or supplements) and let it be distributed there.
Chris recommends 7-15mg of zinc four times a day, away from sources of phytate ("whole grains, nuts, seeds, and legumes") which can inhibit zinc intake.
(At one point he says 10-15mg, and at one point 7-10, but I think this is just bad proofreading. Mostly he says 7-15.)
Conventional wisdom says we can't absorb nearly that much, but Chris thinks we just need more dakka: "the relevant studies have been limited to less than 20 mg/d. Supplementation with 100 mg/d zinc sulfate has been shown to more than double total zinc absorbed from 4.5 to 10.5 mg/d, while decreasing the fraction absorbed from 43% to 9%."
At such high doses, side effects have been observed. "Zinc at 50 mg/d has been shown to lower superoxide dismutase, and at 85 mg/d increased self-reported anemia. Both of these could probably have been averted by proper balancing with copper, which is addressed in the section below. However, the increased need for copper at high zinc intakes reflects increased expression of metallothionein, which can bind to many positively charged metals besides copper." I confess I'm not sure what this "however" is meant to mean. It kind of sounds like "so we still probably shouldn't go that high", but then we go that high anyway. I'm a bit concerned about this.
(I also confess that I have no idea what superoxide dismutase is.)
If you take zinc, you should balance it with copper.
Multi essential: Ionic zinc
This specifically means zinc from the kind of lozenges that work for a cold, or failing that from an ionic zinc throat spray.
(The mechanism that makes this work against a cold will not help with SARS-CoV-2.)
It delivers ionic zinc to the mouth, nose and throat tissues, like we couldn't do with the lungs. Chris recommends using one lozenge a day preventatively; plus several a day on the first sign of symptoms; plus an extra one before and after any potential exposure.
(Question: to be effective against the cold, this delivers ionic zinc to the surfaces of these tissues. Here we want it on the inside. Will that work?)
Daily essential: Copper
Copper surfaces work great against coronaviruses. This knowledge is not super helpful, since we are not copper surfaces.
It does suggest that copper ions in our cells might be toxic to the virus. But this has never been well studied.
Like zinc, copper inhibits papain-like protease 2 of SARS CoV. But it's much less effective at it.
The main reason to take copper is to keep the zinc-to-copper ratio acceptable. It should be between 10:1 and 15:1. (At one point he says 2:1 - 15:1, but again, I think that's bad proofreading.)
Essential if you get sick, before and after exposure: Copper spray
He doesn't actually have loads of detail on this in the report. That was less of a problem in version 1, when he considered it a hedge. Now that he calls it essential, it feels lacking. Fortunately, he's actually written about it publicly in more detail. (Though I think still less detail than the report usually contains.)
He recommends also using an ionic copper spray for the throat infections. This is similar to his recommendation for ionic zinc as well as nutritional zinc, but he doesn't say anything about copper lozenges. I assume those don't exist and/or wouldn't work for some reason. The goal in this case is to get the copper to the surface of the relevant tissues, in hopes that this destroys the virus in much the same way copper surfaces do. It's not clear whether he has specific evidence for this effect (even against other viruses), or just expects it to work based on theory (and if so how robust he considers that theory). Based on what he's written I don't think I'd put this in "essentials" (even acknowledging that "essential" is already an exaggeration).
He doesn't recommend using it daily. Partly because he thinks the effects wouldn't last long enough for that to be worthwhile. (Question: why is zinc different here?) But also partly because he's not convinced it's safe long term. Stop if you notice irritation.
He recommends a specific brand (named in the above link) that seems to have some evidence for short-term safety.
Posted on 29 March 2020
|
Comments
I occasionally make bets about future events. I think I probably should do that more often than I currently do. Given that, I think it's good practice to have a public record of the bets I've made and their outcomes, when available.
I'll try to keep this updated going forward, if I continue to make bets. As of 09-Dec-2024, I'm down £287.96 with eleven wins and eight losses.
(This has nothing to do with the matched betting that I previously wrote about. There I was earning money from sign-up bonuses. Here I'm trying to earn money by being better at predicting the future than other people.)
In order of date I made the bet:
I won: NO on Trump leaving before the end of his first term.
I placed this bet on 20-Oct-2019, on
Betfair,
after a friend said on Facebook that the odds seemed very favorable to him. The odds at the time were 1.3, giving an implied probability of ${1.3 - 1 \over 1.3} = 30\%$ that he'd leave. I bet £50 against this, giving me £15 profit if he doesn't. (Minus commission, so £14.25.) As of 19-Mar-2020 the odds are 1.12, for an implied probability of 11% that he'll leave. (I could cash out now, taking my £50 back immediately and £7.56 minus commission when the market closes. I'm not inclined to do that.)
I lost: NO on a large increase in working from home.
LessWrong user Liron said:
I also bet more than 50% chance that within 3 years at least one of {Google, Microsoft, Facebook, Amazon} will give more than 50% of their software engineers the ability to work from home for at least 80% of their workdays.
I took him up on this for $100 each. We confirmed on 02-Jan-2020. I don't think I'd heard the term "coronavirus" at the time.
This cost me $100 (£92.69 over Paypal, which I think included £2.99 transaction fee). But I got a bunch of LW karma for it. Swings and roundabouts.
I won: YES on someone contracting Covid-19.
In a Telegram group chat I'm in, I bet another member €30 each that at least one person in the chat would contract Covid-19 by 28-Feb-2021. (We made the bet on 28-Feb-2020.)
As of first writing this post: I wasn't confident of winning at the time, and I'm still not. Confirmed infection rates are lower than I'd anticipated - for example, Hubei has had just over 0.1% of its population confirmed as having had the disease at one point, and Italy just over 0.05%.
I think an ambiguous result is more likely than I used to, because people who get mild cases of the disease often aren't tested.
Resolution: I won this some time in November 2020, and my friend paid me what in Sterling turned out to be £25.89.
I won: DECLINE in Trump's odds of being re-elected.
On 04-Mar-2020, I noticed that the betting markets' odds on Trump's re-election had gone up since Covid-19 became a thing. (According to Election Betting Odds, rising from about 40% mid-november to about 56% at the time.) At the time, the number of officially diagnosed cases in the US was very small. I predicted that as the official number rose, and as it became more widely known that the CDC and FDA had basically fucked up, the odds would drop again.
The obvious objection was: "if you can predict that happening, so can anyone. Why haven't the odds changed already?" I didn't have an answer for that, but the stock markets had seemed to react slowly to the news so maybe it would happen here too. (And the next obvious objection was: "oh, so you're expecting the same thing to work twice in a row?" I didn't have an answer for that either.)
Less obvious objections that I realized/someone pointed out after I'd made the bet:
- Bush's popularity rose after 9/11.
- Covid-19 seems to play very nicely into Trump's anti-immigrant, anti-globalist narrative.
In any case, I went ahead. Again on Betfair, I bet £100 against Trump at odds of 1.76. The odds started to drop pretty soon after that. Two weeks later, on 18-Mar-2020, I cashed out (by betting £110.26 for Trump at odds of 2.1, but actually by pressing the "cash out" button). I've claimed my initial £100 back, and no matter who wins I'll earn £21.29. (£20.23 after commission, but nothing if the market is voided.)
I won: BIDEN to win the 2020 election.
On 05-Sep-2020, I put £30 on Biden at the same market as my previous Trump bets, at odds of 1.98 (implied probability ~51%). At the time, FiveThirtyEight, Metaculus and Good Judgment Open all gave Biden at least 65% to win (with different caveats). I have no strong opinion; my bet was on the basis that I think I trust those predictors more than I do the market. If the market gets more in line with what they're saying, I may cash out, whether I'm up or down at the time.
Note that Betfair settles the market according to projected Electoral College votes. A faithless elector, or an incumbent refusing to stand down, don't affect the result. My interpretation is that 538 and Metaculus are also trying to forecast that, so that's not the source of the difference. (I can't see any fine print on GJ Open.) I can think of a few other possible sources:
- People might misunderstand the Betfair rules. (Or the Metaculus ones, but that's close to 538's forecast, the fine print is much more obvious there, and it has a comment thread.)
- I think 538 is modelling under the assumption that Biden stays in the race until the election. If he doesn't, I think including if he dies, I lose my bet. But the Metaculus and GJO forecasts aren't conditional on that (they don't mention Biden at all).
- If a Trump victory would raise the value of GBP compared to a Biden victory, the Betfair market will exaggerate Trump's chances of victory. Lowering the value of USD might work, too. Or if people just want to hedge against a Trump victory.
But I don't really expect that any of these explains it.
Resolution: Biden won the election. I won £29.40 before commission, £27.93 after.
I won 3, lost 3: VARIOUS 2020 US presidential election markets.
On 25-Oct-2020, I placed four more bets:
- £500 on Biden to win overall, odds of 1.47 giving me £235 if I win (plus the £50.71 I already had on him). 538 at the time gave Biden 87%.
- £50 on Democrats to win Pennsylvania. Partially matched at 1.47 and partially at 1.48, I'll get £23.64 if he does. 538 gave this 86%.
- £50 on Democrats to win Florida. Specifically, £48.71 against Republicans, since I got slightly better odds that way, partially matched at 1.98 and partially at 1.97. I'll get £50 if the Democrats win. 538 gave this 67%.
- £50 on Democrats to win Texas. Implemented as a combination of a bet against the Republicans at 1.45, and a bet for the Democrats at 3.2, because that gave me a few pennies extra profit which probably weren't worth the effort of writing this. If Democrats win I'll get £110.64. This is an implied probability of 31%, which is only a little below 538's 37%. But Less Wrong commenter Liam Donovan recommended it, and I figured why not. (I didn't do any actual research myself, and I hadn't seen any of the follow up comments at the time.)
I didn't choose Pennsylvania and Florida by any particularly rigorous search process, I just vaguely remembered hearing that they were good choices.
Then on 05-Nov-2020, I put another £49.63 on Biden to win the election, at odds of 1.10. (That was the amount I had in Betfair at the time.) I was pretty confident this was a damn good bet, but nervous about increasing my exposure enough to really take advantage of it. I somewhat regret this in hindsight.
Then on 08-Nov-2020, I also placed £10 against Republicans to win Alaska, at odds of 1.04, winning £250 if the Democrats won. I didn't think that was likely, but I wasn't sure it was that unlikely, and I thought maybe if mail-in votes leaned Democrat, even if it wasn't enough to take the state it might be enough to cash out at higher odds. Honestly this was probably a bit silly.
Resolution: Biden won the election (£235 + £4.96 to me, £227.96 after commission) and the Democrats won Pennsylvania (23.64 to me, £22.46 after commission). I lost the others.
Overall this set of bets earned me £117.96, and overall my bets on the presidential market specifically (including from September and March) earned me £276.14. (Because commission is calculated on all of them together, rounding errors make that £0.02 higher than you get by calculating my profit on them individually.)
I won: NO on Trump leaving before the end of his first term.
Also on 25-Oct-2020, I put another £100 on Trump lasting his term, at odds of 1.08. I'll get £8 if he does (plus the £15 I already had).
I won these bets on 20-Jan-2021, after what was certainly a sequence of events. I didn't even have to pay commission on them: I'd placed a bet in the opposite direction on someone else's behalf, so according to Betfair I made a loss but according to me I earned £23.
I won: NO on Brian Rose to win the London Mayoral election.
Brian Rose ran for Mayor of London in 2021. On 4-May-2021 I bet £940 against him at odds of 95, giving me £10 (£9.50 after commission) if he didn't win.
I didn't know much about him, but I had seen him boast about his betting odds in ads and on an instagram post I found through google. So I assumed his supporters were adding dumb money to the markets, rather than him actually having a 1% chance of winning. (And Vitalik Buterin points out (section "capital costs") that a small amount of dumb money can cancel out a lot of smart money.)
He did not win.
I won: YES on Ethereum to switch to proof of stake.
On 3-Jun-2022 (or possibly the day after), I bet £50 against £50 from my older brother that Ethereum would switch to proof of stake within two years.
If there was a fork, with people mining on both the original chain and the proof-of-stake chain, and no consensus about which was the "real" Etherum, then this would be a loss for me.
I didn't get around to adding this to this log until October, at which point I discovered that I'd won. The switch happened on 15-Sep-2022 with no controversy I found from a quick search. My brother agreed and sent me the money.
Unresolved: YES on UFOs being ultimately prosaic
On 13-Jun-2023, someone offered on LessWrong to place bets about whether the whole UFO thing that's apparently going on right now is ultimately prosaic in nature or not.
I haven't really been following what's going on and haven't looked closely at the evidence either way. I offered 50:1, my \$5,000 against their \$100. They accepted and sent me \$100 on 23-Jun-2023. (Specifically, 0.00334057 BTC which at the time was worth give-or-take \$100 or £78.42.) If I become convinced by 23-Jun-2028 that not all UFOs are ultimately prosaic, I'll send them \$5,000. Details in linked post.
I won one, lost four: VARIOUS 2024 US presidential election markets.
Specifically, BIDEN to be Democratic nominee; a MALE to win the election (cashed out early taking a loss); BIDEN to win the election; and HARRIS to win the election.
On 29-Nov-2023 I bet on Joe Biden to be the Democratic nominee in the 2024 election. I put £200 up at average odds of 1.44, giving me £88.85 (£84.41 after commission) if I won. The bet was split between odds of 1.44 and 1.45, with implied probabilities of 69% (nice) for both of those.
Also on 29-Nov-2023 I bet £300 that the gender of the election winner would be male. £300 at average odds of 1.15, giving me £43.59 (£41.41 after commission) if I won. The bet was split over odds between 1.12 (implied probability 89%) and 1.17 (85%). (At the time, most of the 10-15% was Nikki Haley, and I thought she was overpriced.)
On 03-Mar-2024 I bet £100 that Biden would win the election. I would have got £272.31 (£258.69 after commission) if I'd won. Average odds 3.72, split over 3.7 and 3.75 (both with implied probability 27%).
Then on 11-Nov-2024 I cashed out of the gender market. I took out £206.47, so I lost £93.53 on this market. This was essentially a bet of £137.11 on Harris winning at odds between 2.5 (40%) and 2.52 (40%). If I'd placed the bet on the actual election winner market, I might have got better odds, but I'd have had to pay commission on profits.
Then on 22-Nov-2024 I bet £100 that Harris would win the election at odds of 2.54 (39%). I would have got £154 if I'd won (£146.30 after commission).
So overall I lost 4/5 bets and £493.53.
Open bounty: $5,000 for responsibly ending Malaria
This is a bounty, not a bet. But it seems good to have an easy-to-find record of it, and I don't have somewhere more suitable.
On 24-Sep-2022, LessWrong user lc announced a $5,000 bounty for any person or team who responsibly reduces annual global mortality from Malaria by 95% or more. Details in linked post. Various other people added to that pot, and on 01-Oct-2022, I committed $5,000 to it myself.
Posted on 19 March 2020
|
Comments
I'm one of those people who feels personally called out by xkcd's "Duty Calls" ("someone is wrong on the internet").
(Not as much as I used to. At some point I stopped reading most of the subreddits that I would argue on, partly for this reason, and Hacker News, for unrelated reasons, and now I don't do it as much.)
As pastimes go, there's nothing particularly wrong with internet arguments. But sometimes I get involved in one and I want to stop being involved in one and that's not easy.
I could just, like, stop posting. Or I could let them say something, and then respond with something like, "yeah, I'm still not convinced, but I don't really have time to get into this any more". But then the other person wins, and that's terrible. It potentially looks to onlookers like I stopped because I couldn't find something to say any more. And in at least some cases, it would feel kind of rude: if they've put a lot of thought into their most recent post, it's a bit dismissive to just leave. In the past, when people have done that to me, I've disliked it, at least some times. (Well, at least once. I remember one specific occasion when I disliked it, and there may have been others.)
Another thing I could do is respond to their most recent post, and then say "and now I'm done". But that feels rude, too, and I certainly haven't liked it when people have done it to me. (Why not? It puts me in the position where I don't know whether to respond. Responding feels petty, and kind of a waste of time; not responding feels like they win, and that's terrible.) If they do reply, then I'm shut off completely; I can't even make a minor clarification on the order of "no, you somehow interpreted me as saying exactly the opposite of what I actually said".
So I don't like those tactics. There are probably mental shifts I could make that would bring me more inclined towards them, but… about a year ago I came up with another tactic, which has seemed quite helpful.
What I do now is say something to the effect of: "after this, I'm limiting myself to two more replies in this thread."
This has various advantages. It feels less rude. It doesn't look like I'm quitting because I have no reply. It helps the conversation reach a more natural conclusion. And it also feels a lot easier to do, partly for the above reasons and partly for the normal reasons precommitment helps me to do things.
For some quantitative data, I went over my reddit history. It looks like I've used it ten times. (I don't think I've ever used it outside of reddit, though I initially thought of this after an argument on Facebook.)
- "(This doesn't seem super productive, so I'm going to limit myself to two more relies in this thread.)" This was my third comment, and we each made one more afterwards.
- "Limiting myself to two more replies in this thread." This was my third comment, and afterwards, I made two more and they made three more. Their final two replies got increasingly rude (they'd been civil until then), but have subsequently been deleted. This is the only time I ran into the two-more-comments limit. Also, someone else replied to my first comment (in between my final two comments in the main thread) and I replied to that as well.
- "I find myself getting annoyed, so I'm limiting myself to two more replies in this thread." This was my fourth comment, and afterwards we made each made one more. (This was the only person who questioned why I was continuing to reply at all. A perfectly reasonable question, to which I replied "not going down this rabbithole".)
- "(Limiting myself to two more replies in this thread.)" This was my third comment, and afterwards we made two more each. If their final comment had come after I hit the limit, I would have been tempted to reply anyway. (Uncharitably paraphrased: "oh, we've been talking past each other, this whole time I've been assuming X and you've been assuming Y, which is very silly of you" / "well I explicitly said I was assuming Y and not X in my very first post in this thread, and even if we assume X and not Y your behaviour still makes no sense".) All of their comments in this thread have since been deleted.
- "Pretty sure this is all a big waste of time, so I'm limiting myself to two more replies in this thread." This was my sixth comment linearly, but only second in reply to this specific user, and I'd previously made another two in different subthreads below my first comment. Afterwards, the person I'd been most recently replying to didn't make any more comments. But someone else replied to this comment, and I replied to them; and two other people replied in those other subthreads, and I replied to both of them as well (but one of those replies was just a link to the other).
- "Limiting myself to two more replies in this thread." This was my fifth comment, and neither of us replied afterwards, though I did quickly edit this comment to add a clarification that arguably could have counted as its own comment. Someone else replied to one of my comments higher up the chain, and I replied to them.
- "(I don't want to get sucked into this, so I'm limiting myself to two more replies in this thread.)" This was only my second comment, and neither of us replied further.
- "(Limiting myself to two more replies in this thread.)" But in their next reply, they made a mistake that I had previously explicitly pointed out. So instead of replying in depth, I said, "It's quite annoying that you continue to misunderstand that, so I'm out." They replied saying "I think you're struggling to justify your initial comments and that's why you're "out", but that's fine. I accept your unconditional surrender." I didn't reply further. Since it was /r/science, and I was quite miffed, I reported this comment as unscientific to see if it would help me feel better. I don't remember if it worked. The comment did not get removed.
- "I think I'm going to reply at most twice more." This was my fifth comment, and neither of us made any more afterwards. Their first and final comments are still there, but their other three have been deleted.
- "I'm going to limit myself to two more replies after this." This was my third comment, plus I'd made one in another subthread below my first comment. Afterwards we each replied twice more.
In thread #5, I made 11 comments in total; but in others, my max comment count was 6. This feels like I mostly did a decent job of not getting sucked in too deeply. And since I generally got the last word in (threads #2 and #7 were the only exceptions), I think (though I don't specificly remember) I rarely had the feeling of "if I don't reply now then they win and that's terrible". Thread #7 is the only one I think I still feel lingering resentment about. From before I thought of this tactic, I can think of at least two arguments where I didn't get the last word and I still feel lingering resentment. (One is the argument that triggered me to think of this tactic.)
So generally this seems like a success. Ideally we'd compare to a world where I didn't think of this tactic, but I'm not really sure how to do that. (We could go over my reddit arguments where I didn't use it, but that's clearly going to have sampling bias. We could go over my reddit arguments from before I thought of it, but we can't know when I would have used it or how things would have progressed. Possible experiment: going forward, each time I want to limit my future replies, I toss a coin for whether I actually do it in that comment. Keep track of when I did this. I am unlikely to actually run this experiment.) For a way it plausibly might not have been a success: I suspect it's the case that having limited my total investment, I spent more effort on many of these comments than I would have otherwise. If these arguments would have ended just as quickly in any case, then this tactic caused me to spend more time and effort on them.
I'm a bit surprised that I only ran into the two-more-comments limit once. A part of me would like to interpret that along the lines of: once I started putting more effort into my comments, I demolished my opponents' arguments so thoroughly that they accepted defeat. But this seems unlikely at best.
I will say that none of these comment chains felt like collaborative discussions. Some of them started that way, but by the end, they all just felt like "I am right and you are wrong". (This is not very virtuous of me, I admit.) My thinking had been that this tactic would be most valuable in collaborative discussions. But it seems I don't have many of those on reddit, at least not ones that I spend much time on. So, no direct evidence on that yet.
I'm not sure how to handle replies to other people, or replies in subthreads other than the main one. A strict wording would suggest that I should count subthreads against the limit, but I haven't so far and it hasn't caused me problems. Even a weak wording would suggest that I should count replies to other users against the limit, but I've only had one of those and didn't reach the limit whether you count them or not.
I'd ideally like to have a get-out clause like "…unless I actually decide that replying after that is worth my time". But I'm not quite sure that's the "unless" that I want. (Plus it seems kind of rude, but it's not like I'm being super polite as-is.) Anyway, I haven't needed that clause yet.
Posted on 05 December 2019
|
Comments
I don't like writing tests in Elm. Naively, it seems like the fact that all Elm functions are pure would make it easy. But I've still never really been able to test the things I really want to.
It's possible that I'm not very good at writing tests in general. But even if that's true, I don't think it's the whole story.
I have another hypothesis, which is: much of the reason is that although Elm functions are pure, in the sense of "given the same input, they return the same output" - they aren't necessarily transparent, in the sense of "you can look at the output and verify that it's correct".
To recap, I would describe the Elm architecture as consisting of:
-
Model - a type describing the data you're interested in. This is usually mostly transparent. There are some opaque blobs where components haven't exposed their internals, but I think those mostly aren't the kind of opacity that gets in the way.
-
Msg - a type describing the messages your app passes around. Again, mostly transparent, with opaque blobs where components haven't exposed their messages. I feel like this opacity is maybe a bit more annoying, but still not very.
-
update : Msg -> Model -> (Model, Cmd Msg) - a function describing the logic of your app (or whatever it is you're architecting). The Model and Msg are still transparent, but the second return value is a Cmd Msg which is completely opaque, and which is the main source of the problem.
-
view : Model -> Html Msg - a function describing the rendering of your app. Html Msg is also arguably opaque, but you can inspect it using elmer, or (as I discovered while writing this post) the Test.Html modules in the test package. I'm not sure if you can inspect it as deeply as you might want, I haven't explored these much yet.
Now, in my experience, a lot of the logic in an app is contained in the way the update function chains. "After receiving this message, we send a command which eventually results in receiving that message, and then we want to put some value in the model." And we can't test those chains, because Cmd is opaque. So that's part of why I haven't liked writing Elm tests.
But I think I've found a method that will help, at least somewhat. You don't need to rewrite anything except your update function, and I actually think it's a mild improvement even if you ignore testing. I call it the Effect pattern.
We've implemented this pattern at work, in a couple of places. When I first did so, the first two tests that I wrote both revealed bugs in my code. (I think I'd known about both of those bugs but forgotten them. I wasn't consciously expecting the tests to fail.) Neither of those tests needed to be updated when I fixed the bugs. I think this is a good sign, but it's not very strong evidence. Beyond that, I mostly have theory.
Example
I'm going to demonstrate with a simple app. It'll be buggy, and the bug will be hard to test for. Then I'm going to refactor the app to make it more testable, and write a test. Then I'm going to fix the bug, and verify that the test now passes. I think the app is too simple to make the benefits really obvious, but hopefully I can convince you anyway.
So here's the app. It has a number, and a button to increase the number by one, and a button to multiply it by two. When you press one of those buttons, the number gets "saved to the server"; normally that would be an http request, but we emulate that by just sending a time delayed response. There's a message telling you whether the number has been successfully saved yet.
Actually, most of the app supports increasing the number by any integer, and multiplying it by any integer. That's not implemented in the view though. The Watsonian explanation for this is that the developer has a habit of overengineering things. The Doylist explanation is that it makes the interesting bits more interesting, but not significantly more complicated; and the view code is boring.
The bug is: if you press buttons quickly, the "saved" message will temporarily be wrong. You've sent two messages to the server, and one hasn't come back yet; the number that's been saved is not the number on display. Silly, but I think it works as a demonstration.
(There are surely also bugs related to the size of numbers, but I'm not interested in those right now. Additionally, a real life server would have other problems like "sometimes requests will fail" and "sometimes requests will be handled out of order"; the second in particular is hairy, but I haven't emulated these possibilities.)
Here's the update function:
update : Msg -> Model -> (Model, Cmd Msg)
update msg model =
case msg of
IncBy n ->
( { model | count = model.count + n, saved = False }
, fakeSaveCount (model.count + n)
)
MultBy n ->
( { model | count = model.count * n, saved = False }
, fakeSaveCount (model.count * n)
)
Saved ->
( { model | saved = True }, Cmd.none )
You can probably guess roughly what Model and Msg look like just from that.
As written, how would you test for the bug? I think the way to do it is to write a wrapper update1 msg model = Tuple.first <| update msg model that ignores the Cmd. Then test that
initialModel
|> update1 (IncBy 1)
|> update1 (IncBy 1)
|> Saved
|> .saved
is False. And that works to detect the bug, but you need to know exactly what messages get sent in response to IncBy 1. In this case that's easy. In more involved cases, you'll need to know it for every Msg constructor, and you're going to make a mistake.
Here's how I'd rewrite for testability:
type Effect = ESaveCount Int
update : Msg -> Model -> (Model, Cmd Msg)
update msg model =
let (newModel, effs) = updateE msg model
in (newModel, Cmd.batch <| List.map (\e -> runEffect e model) effs)
updateE : Msg -> Model -> (Model, List Effect)
updateE msg model =
case msg of
IncBy n ->
( { model | count = model.count + n, saved = False }
, [ESaveCount (model.count + n)]
)
MultBy n ->
( { model | count = model.count * n, saved = False }
, [ESaveCount (model.count * n)]
)
Saved ->
( { model | saved = True }, [] )
runEffect : Effect -> Model -> Cmd Msg
runEffect eff _ =
case eff of
ESaveCount n -> fakeSaveCount n
That is, we split it into two parts. One part updates the model, and describes the side effects transparently. The other part turns the transparent side effects into opaque ones.
Even if we're not testing this, I kind of like it. It's nice to have a complete list of possible side effects in one place, where it isn't mixed in with model updates. But I do also want to be able to test it. Obviously, now we test updateE instead of update. Is that any better? I think so.
Here's a simple example of something we can now test that we couldn't before: "whenever update changes model.count, it makes a server request to save the new value; and whenever it makes a server request to save a value, that value is now in model.count." (We may need to write fuzzers for our Msg and Model to do this.) To do this, we need to trust that runEffect works properly, that ESaveCount actually generates a server request; but I think that's a fairly okay thing to trust.
But that's small fry. I spoke above about chaining the update function, and that's harder. If you're going to do it properly, you still need to know what messages get sent in response to every Effect constructor, and you can't learn that from calling the function. But I still think this is an improvement: if done right, I would expect (and my limited experience agrees) that typically Effect will have many fewer constructors than Msg, and for each one, the transformation to messages is fairly simple.
Here's a helper function that you can use to test updateE:
runUpdates
: (state -> msg -> model -> (state, (model, List effect)))
-> (state -> effect -> model -> (state, List msg))
-> state
-> model
-> List (List msg)
-> (state, model)
runUpdates updateE runEffect initialState initialModel messages =
let go = runUpdates updateE runEffect
in case messages of
[] -> (initialState, initialModel)
[] :: moreMsgs -> go initialState initialModel moreMsgs
(msg1 :: moreMsgs1) :: moreMoreMsgs ->
let (newState1, (newModel, effs)) =
updateE initialState msg1 initialModel
(newState2, newMsgs) =
List.foldl
(\e (s, m) -> runEffect s e newModel
|> Tuple.mapSecond ((++) m)
)
(newState1, [])
effs
in go newState2 newModel ((moreMsgs1 ++ newMsgs) :: moreMoreMsgs)
On a high level, the way it works is this: you pass it your regular updateE function and a mocked runEffect function, together with an initial model and a list of messages to send. The messages get sent, one at a time, to the model. Any effects caused by updateE are handled by the mock runEffect, which returns a list of additional messages to be sent in future. We keep running until there are no more messages.
There are two complications. One is that we also thread through some arbitrary state, that can be updated both by updateE and runEffect. We'll see the value of that later, but if you don't need it,
stateless : (a -> b -> c) -> (() -> a -> b -> ((), c))
stateless f () a b = ((), f a b)
is a helper function that lets you forget about it.
The other complication is that we pass in a nested list of messages. That's to give us some control over timing. Any messages returned by runEffect will be handled after the current "batch" of messages, but before the next "batch". So if you want to test the sequency "run msg1, then msg2, then handle the results of msg1", you would pass in [[ msg1, msg2 ]]. If you want to test the sequence "run msg1, handle its results, then run msg2", you would pass in [ [msg1], [msg2] ].
I have a feeling this won't always be enough control, and in future the mocked runEffect will need to return List (List msg) in place of List msg. (With the first item being messages to run immediately, the second being items to run between the current and the next batch, and so on. You'd get the current behaviour by returning [ [], msgs ].) But it suffices for now.
And here's one way to test the app:
type alias TState = (Int, List Expectation)
testSave : Test
testSave =
let
mockUpdateE : TState -> Msg -> Model -> (TState, (Model, List Effect))
mockUpdateE (n, exps) msg model =
let (newModel, effs) = updateE msg model
newState = case msg of
Saved ->
( n - 1
, (newModel.saved |> Expect.equal (n - 1 == 0))
:: exps
)
_ -> (n, exps)
in (newState, (newModel, effs))
mockRunEffect
: TState
-> Effect
-> Model
-> (TState, List Msg)
mockRunEffect (n, exps) eff model =
case eff of
ESaveCount _ -> ( (n+1, exps), [Saved] )
in
test "Doesn't pretend to be saved" <| \() ->
let ((_, exps), _) =
runUpdates mockUpdateE mockRunEffect (0, []) initialModel
[[IncBy 1, IncBy 1]]
in Expect.all (List.map (\e () -> e) exps) ()
I admit, this is pretty ugly. But I think it's conceptually quite simple. The state keeps track of two things: how many save requests are currently "in flight", which gets updated as we step through; and a list of assertions, which we verify at the end. Every time we send a request (with ESaveCount), we increase the in-flight count. Every time we receive a Saved message, we decrease it, and add a new assertion to the list: model.saved should be True iff there are no requests remaining in-flight.
You can see this version of the app here. Note that to avoid the hassle of playing with Test.Runner, I've replaced the Test with an Expectation by commenting out the test "..." line (but nothing underneath), and put the result in the view. You can remove the second IncBy and check that it now passes (because if there's only one IncBy, the bug doesn't exhibit).
Now to fix the bug, and see what effect that has on the tests. If you can't fix a bug without changing the tests you wrote for it, that's a bad sign about your tests.
The test uncovered the bug by keeping track of some additional state. So the obvious thing to do is to move that state into the model. Count the number of requests in-flight, and only count as "saved" if there are none. In fact, we no longer need saved as a field at all; as written in the test, saved is true iff there are no in-flight requests.
(This doesn't work in the real world, where requests can fail. I think it's fine as a demonstration.)
Removing saved actually does mean we need to rewrite the test. But only minorly, and we can do that before fixing the bug. All we need is to replace the reference newModel.saved with isSaved newModel where isSaved = .saved. Then when we fix the bug, we rewrite that as isSaved m = m.inFlight == 0, and the test passes with no more changes. We'll want to use that function in the view anyway. (Avoiding this kind of thing is one reason people like to write opaque models.)
You can see the fixed version of the app here.
However… now that we've put that state in the model, although the test still works, it's looking a bit silly. We've got some state in the tests that should always be identical to the state in the model; why not just test that the model is updating the state correctly?
So here are some other tests that we could write (but that I'm not going to, for time reasons):
-
We could test that, given the same messages as above, the model doesn't become isSaved until the very end of runUpdate. We can still do that with runUpdates; our state parameter is now List Model, we use mockUpdateE to keep track of every intermediate model (and mockRunEffect no longer needs to deal with state at all), and then finally verify that isSaved is false for all but the last. (This test we could have written with the old model. As described it fails if, in future, Saved starts having other effects - maybe it wants to send something to a port. We can get around that by doing more bookkeeping, but we could also simply decide that mockRunEffect will pretend it doesn't have those effects.)
-
We could test that any update which returns an ESaveCount also increases inFlight; and further, that any messages sent in response to ESaveCount will decrease inFlight. I think this test is most valuable if it uses a mocked runEffect that's also used in other tests.
Really though, I'm not sure what's best. I do think the Effect pattern will help.
Further thoughts
We haven't used this much yet, so there's a lot left to explore. Here are some thoughts I've had, but not developed very far, in no particular order.
Nomenclature. We've gone from update to update, updateE and runEffect. I currently think runEffect is an okay name, but I feel like with no historical baggage, the name update would have gone to updateE. Then what would update be called? I left it as-is partly to avoid stepping on historical toes, and partly because I don't know. runUpdate? That would give us the pattern "update functions update the model and return some kind of what-next value, run functions produce Cmds". (Of course, runUpdates violates that pattern. Maybe that should become foldUpdate…?)
Also, we'll want a helper function to convert updateE and runEffect into the correct form. What do we call that function? The only sensible suggestion I have is liftUpdate, but I'm not sure I like it.
Randomness. The test I've demonstrated was deterministic. So have all the tests I've written for Effect so far. (At least one used a fuzzed input, but that doesn't feel like it counts.) To get randomness I imagine you'd need to put a Seed in the state parameter of runUpdates, and then use Random.step (maybe with Test.Runner.fuzz to get you the Generator that you need).
Simpler test helpers. runUpdates is quite complicated, and as mentioned, I suspect it'll need to be even more so. I think most tests probably won't use all of its features. What simpler variants of runUpdates are worth creating (and what should they be named)? An obvious candidate is a variant with no state. Maybe also a variant that returns a list of models instead of just the final model.
Full state machine. In Haskell we use quickcheck-state-machine, which I really like. Could we do something similar in Elm? I think it would be possible, though probably looking quite different. Elm doesn't have all of the type-level features that QSM relies on, but it also doesn't have all of the features that QSM needs to support.
Should runEffect see the model? Reasons yes: it simplifies the Effect constructors; it reduces total amount of code; it allows one stateless function to work with both updateE and runEffect. Reasons no: it gives runEffect more rope to hang you with (more likely to be complicated, more likely to diverge in the codebase and test suite). We went with yes because in one of our components, many constructors would have needed many parameters. But we probably could have refactored a little so that many constructors would have needed only one parameter each.
Can you reuse mocked runEffect functions? I touched on this above. That is, will you be able to write just one or two per component and use those in most of the tests for that component? (If not directly, then just wrapping them in some state-updating code that doesn't change the Msg they return.) Or will each test need a separate one? I certainly hope you can reuse them. If not, that might diminish a lot of the value. The fewer you have, the easier it is to keep them all correct when the real one changes.
(What if you have a potentially large number of functions, but selected by a configuration parameter? I think depending on how this is handled, it could be closer to either end of the scale.)
Composability. A component using this pattern can be embedded in one that doesn't, no problem. You just don't get any of the benefits in the parent.
What if you embed a non-Effect component in an Effect component? This forces you to put some Cmd in your Effect type. How do you test that? I'm not sure you reasonably can. So far I think we've just avoided testing those parts of our components.
What if you embed an Effect component in another Effect component? In the codebase, I imagine your parent's Effect type has a constructor ChildEffect Child.Effect which in turn calls Child.runEffect. That lets you test the parent component, but… you may need to mock runEffect for every child component, and that doesn't sound fun. (If the mocked functions do turn out to be fairly reusable, maybe not so bad.)
Also, if you want to provide an Effect component in a library, you may want the Effect type to be opaque (like Model and Msg often are today). But then if you want people to be able to test your component in theirs, maybe that makes you responsible for providing suitable mocked runEffect functions.
Unconventional updates. I've been assuming your existing update function has type Msg -> Model -> (Model, Cmd Msg). But a lot don't. A common pattern is something like Msg -> Model -> (Model, Cmd Msg, MsgToParent) where MsgToParent is something that the parent may need to act on. (In our case, it's often just global state that needs to be sent back up in turn.) How do you handle this kind of thing?
In the codebase, I think the correct decomposition for this is still to change only the Cmd Msg return value, since that's the only opaque one, and for runEffect to be the same as it would be otherwise. (You could give it MsgToParent as an extra parameter, but like with Model that won't give you any extra power. By default I wouldn't do it, but I don't think it would be an obviously bad idea.) If you had two opaque return values… honestly I don't think I've seen this and I don't think I want to speculate about what to do in that situation.
In the test suite, you won't be able to use the existing runUpdates function. What to do instead? It might prove useful to have a runUpdates3 (or something) which can handle this case, but I'm not sure exactly how that would work.
Another possibility would be using wrappers to put your updateE in the right shape. For example, maybe you can do type EffectOrMsg = Effect Effect | MsgToParent MsgToParent, and then combine the final two results of updateE. I don't know if that would always get you what you want.
tl;dr
You can take your existing function update : Msg -> Model -> (Model, Cmd Msg), and decompose it into two others:
updateE : Msg -> Model -> (Model, List Effect)runEffect : Effect -> Model -> Cmd Msg
defining the new Effect type as whatever makes this decomposition work nicely. I think this is a slight improvement in the codebase; and independently of that, I think it helps you to write better tests.
See also
Delayed update, 13-Mar-2021: A commenter on /r/elm points out that elm-program-test does something similar. It looks like you use it by rewriting your program in basically the same way I recommend here, and then it implements a bunch of test helpers you can use on top of that. If you're interested in this direction, I recommend checking it out.
Posted on 20 October 2019
|
Comments
(I've been editing this post on and off for almost a year. I'm not really happy with it, but I suspect I never will be.)
Several months ago I gave a talk at work about Hindley-Milner type inference. When I agreed to give the talk I didn't know much about the subject, so I learned about it. And now I'm writing about it, based on the contents of my talk but more fleshed out and hopefully better explained.
I call this a reckless introduction, because my main source is wikipedia. A bunch of people on the internet have collectively attempted to synthesise a technical subject. I've read their synthesis, and now I'm trying to re-synthesise it, without particularly putting in the effort to check my own understanding. I'm not going to argue that this is a good idea. Let's just roll with it.
I'm also trying to tie in some quasi-philosophy that surely isn't original to me but I don't know if or where I've encountered it before.
Background
When people write software, sometimes it doesn't do exactly what we want. One way to find out is to try running it and see, but that's not ideal because any complicated program will have way too many possible inputs to test. (Especially when you consider that inputs include things like "amount of free space on disk" and "time taken for a web server to respond to a request".) So it would be nice if we could mathematically prove whether our software does what we want, without actually running it. Can we do that?
That's not a very well-defined question, but we can ask more precise versions of it. Here's a well-known one: given some possible input to our software, we might want to prove that our software will eventually stop running. Can we prove that?
That question is known as the halting problem, and the simple answer is that we can't, not in general; the halting problem is undecideable. But the full answer is more complicated.
To solve the halting problem, we want a program that, when shown another program and some input to be fed to that program, satisfies three different conditions:
- It will always return an answer.
- The answer will always be either "yes, this always terminates" or "no, sometimes this doesn't terminate".
- The answer is always correct.
And that's not possible. But we can compromise on any of the three. We can make a program that sometimes doesn't return an answer, or one that sometimes gets the answer wrong. But perhaps most interestingly, we can make a program that sometimes says "I don't know".
And when you allow that answer, you can create a language on which the halting problem is decideable. You can write a program that will tell you truthfully whether any program written in that language will terminate; and for any other program, will say "I don't know". (Perhaps expressed in words like "syntax error on line 1".)
Now, the halting problem is tricky. It turns out that if you create a language like that, there are a lot of interesting things that programs written in that language just won't be able to do; the language will necessarily be Turing incomplete. But there are also lots of interesting things that they can do. To give three examples of such languages:
- Regular expressions are really useful for certain operations on strings, but that's about all they're good for.
- SQL is really useful for working with databases. According to some people on stack overflow, the ANSI SQL-92 standard was Turing incomplete and the ANSI SQL-99 standard is Turing complete. (No mention of the SQL-96 standard that came between these, but reading between the lines, probably Turing incomplete.) If I understand correctly, the feature required to make SQL-99 Turing complete is one I've literally never used; so for my purposes, it may as well be Turing incomplete.
- Coq is used for proving math theorems. It's an interesting one because when you write your program, you have to also provide a proof that your program terminates. (I think this is slightly false, but again, good enough for the point I'm making.)
So although these languages can't do everything, they can still be incredibly useful in their domains. More useful than a more general purpose language might be. One reason for this is that being able to prove non-termination is a useful property of the language. If you had to write a SQL query in C, it would be all too easy to write some C code that would accidentally loop forever.
I'm trying to illustrate here something that seems to me important, which is that there's a tradeoff between what I'll call expressiveness and legibility. A programming language is expressive if you can easily write many interesting programs in it; it's legible if you can easily say many interesting things about the programs you've written in it. And I claim that the most expressive programming languages won't be the most legible, and vice-versa; though there will certainly be languages which are neither expressive nor legible. This tradeoff seems fundamental to me, and I expect that some approximation of it has been proven as a theorem.
I haven't defined these very well, but hopefully some examples will help. I will also clarify that both of them are highly dimensional; and that "raw computational power" is one of the things that expressiveness can point at, but not the only thing; and "human readability" is not really one of the things that legibility points at, but many things that increase legibility will also increase human readability.
-
Perl-compatible regular expressions can classify sets of strings that normal regular expressions can't. But they're harder to make time and space guarantees about. And it's possible to prove whether two regular expressions are equivalent, but that's not possible in general for PCREs (proof: PCREs can encode CFGs; CFGs can't be proved equivalent).
-
Under certain assumptions, Haskell's monadic IO lets you look at the type of a piece of code and know that it won't depend on external state. In return, a function can only bring in external state if its caller allows it to (which requires having permission from its own caller, and so on).
The assumptions in question are false (partly because unsafePerformIO exists), but I've been able to get away with pretending they're true (partly because unsafePerformIO is punishable with excommunication).
-
Custom operators (at least as implemented in Haskell and Elm) are equivalent to named functions, and don't gain or cost much in terms of legibility and expressivity. They simply make code more or less readable. But operator overloading, at least when combined with dynamic typing, gains expressivity at the cost of legibility (you no longer know that a + b will do anything remotely like an addition).
-
Macros make it easier to do things like create DSLs, reduce boilerplate, and set compile-time config options. But they mean that a function call might not look like one, or vice-versa; expressions might get evaluated many times, or not at all; and the code might perform differently depending on the phase of the moon when it was compiled.
Motivation
So we've got this tradeoff, and in our programming language design we try to navigate it. We try to find kinds of legibility that can be bought for little cost in expressiveness. Or more precisely, we try to find kinds of legibility that we care about, and that can be bought for little cost in kinds of expressiveness that we care about.
And Hindley-Milner type systems are a tradeoff that's proved fairly successful, both in direct use and as inspiration. At my company, we use Elm, which runs on an approximately HM type system. (I don't think it's pure HM, due to extensible record types.) We also use Haskell, which runs on a type system that extends HM in many directions. Haskell's system is more expressive and less legible, but still successful. (I'll mostly be using Elm for examples in this post, and not extensible records.) ML and OCaml are other notable languages based on HM, though I haven't used either.
The legibility HM offers is, roughly, the ability to prove that a program typechecks. I'm not going to clarify exactly what that means, but we probably all have a decent idea. It's the thing that lets the Elm compiler say "no, that program is trying to add a string to an int, bad program", while the Python interpreter doesn't know that's going to happen until it's too late. The Elm compiler will refuse to compile your program unless it can logically prove that it will typecheck.
More precisely, what HM offers isn't type checking but the more general type inference. (And beyond that, type inference in roughly linear time.) Type inference doesn't just tell you whether a program typechecks, but what its type is; a program fails to typecheck iff no type can be inferred for it.
What this means is that there's no need to supply type annotations. And indeed, in Elm you can get away without them, except I think for extensible records. In Haskell you sometimes can't, because Haskell loses some of the legibility that HM offers.
(We typically do supply type annotations, but that's because they're useful. Partly as documentation for humans, partly to help pinpoint errors when our programs fail to typecheck.)
And so in an HM system you get no runtime type errors. And although not all runtime errors are type errors, in many cases they could be. For example, an array out-of-bounds exception isn't a type error. But when designing a language, you can decide that array out-of-bounds exceptions won't exist, any array lookup will return either a value from the array or null. If type errors are possible, you've just eliminated one source of errors by pushing them somewhere else, and possibly somewhere harder to debug. But in HM, you've eliminated one source of errors by pushing them somewhere more visible, where they can be ruthlessly executed.
Elm actually tries to promise no runtime errors, period, provided you stay inside Elm. On one level, I think that's a fairly minor imposition on language design, something you get "for free" by deciding that none of the built-in functions you provide will ever throw a runtime error. On another level, it seems completely impractical to decide for example that cons will return a meaningful value if it can't allocate more memory. I'm not aware that Elm even tries to handle those errors.
(Haskell doesn't try to promise the same thing, and allows functions to return undefined. This is another legibility-expressiveness tradeoff.)
So HM's legibility gain is: type inference, powerful type system, no runtime type errors, optionally no runtime errors at all. It's good.
Meanwhile, the expressiveness cost is that you need to write your programs in ways that the type inference algorithms can work with, which forbids some things that you might like to do.
For example, suppose you want to clamp a number to between -1 and +1. In Python, you could write that like
def clamp(x): sorted([-1, x, 1])[1]
and as long as sorted always returns a list of the same length it started with, that works fine. But it only works because the Python interpreter allows you to be reckless with array indexing. Elm doesn't let you be reckless, and so Elm has no equivalent way to perform array lookup. If you tried to write the same function in the same way in Elm, the result in the compiler's eyes would not be a number but a Maybe number - AKA "either a number or Nothing". (Nothing is roughly equivalent to None in python or null in many other languages, but you have to explicitly flag when it's allowed.) When you actually run this code, you will always get a number and never Nothing. But the compiler can't prove that.
(Again, I stress that you will never get Nothing as long as your sort function always returns a list of the same length it started with. That's something you can prove for yourself, but it's not something the Elm compiler can prove. It's not even the sort of thing the Elm compiler knows can be proven. And so in turn, it can't prove that you'll never get a Nothing here.)
And then the Elm compiler would force you to account for the possibility of Nothing, even though there's no way that possibility could occur at runtime. One option is to pick an arbitrary result that will never be exposed. That works fine until the code goes through several layers of changes, an assumption that used to be true is now violated, and suddenly that arbitrary result is wreaking havoc elsewhere. Or in Haskell, your program is crashing at runtime.
To be clear, that's not significantly worse than what we get in Python, where the code can also go through several layers of changes that result in it crashing at runtime. But we were hoping for better.
And in this case "better" is easy enough, you can just write your function to avoid indexing into a list, and then it can return a number with no need for trickery. The point isn't that you can't do the thing. The point is that (a), even if the thing is safe, the compiler might not know that; (b), if you decide it's safe anyway and find some way to trick the compiler, the compiler no longer protects you; and (c), if you want to do it in a way the compiler knows is safe, you might need to put in some extra work.
For another example, HM type systems can't implement heterogenous lists. So this is really easy in python:
def stringify_list(l):
return [ repr(x) for x in l ]
stringify_list(["hello",
0,
["here's a", "nested list", {"and": "maybe", "a": "dict"}],
"it can even be passed itself, like so:",
stringify_list])
but impossible in Elm. You can sort of get the same effect by creating a type with many constructors
type HeteroType = HTInt Int
| HTString String
| HTBool Bool
| HTList (List HeteroType)
| ...
but it's not quite the same, because it can only accept types you know about in advance. Also, it's a massive pain to work with.
For a third example: Haskell is known for its monads. But Elm has no equivalent, because an HM type system can't support generic monad programming. You can implement the generic monad functions for specific cases, so there's Maybe.map and List.map, but there's no equivalent of Haskell's fmap which works on all monads.
Hindley-Milner type systems
I've talked about the tradeoffs that HM type systems offer, but not what HM type systems actually are. So here is where I get particularly reckless.
This bit is more formal than the rest. It's based on the treatment at wikipedia, but I've tried to simplify the notation. I'm aiming for something that I would have found fairly readable several months ago, but I no longer have access to that version of me.
Also, this part is likely to make more sense if you're familiar with at least one HM-based language. That's not a design feature, I just don't trust myself to bridge that inferential gap.
For an HM system, you need a language to run type inference on, and you need types to run type inference with, and you need some way to combine the two. You could use the language with no type inference, if you didn't mind crashes or weird behaviour at runtime, when you made a mistake with typing. (Haskell allows this with a compiler option.) And you could run type inference without caring about the semantics of the language, treating it as essentially a SuDoku, an interesting puzzle but meaningless. (Haskell supports this, too.) But by combining them, the semantics of the language are constrained by the type system, and runtime type errors are eliminated.
Types
Types come in a conceptual hierarchy which starts with type constants. That's things like, in Elm, Int, Float, Bool, String, Date, (). It also includes type variables, which in Elm are notated with initial lower-case, like a and msg. (Though the type variables number, comparable and appendable are special cases that I won't cover here.)
Next in the type hierarchy is applied types. Here a "type function" is applied to arguments, which are type constants and/or other applied types. These are things like List Int, Maybe (List Float), Result () Date, and a -> String. (In that last one, the type function is the arrow; Haskell would allow you to write it (->) a String. Aside, (->) is the only type that HM specifically requires to exist; a -> b is the type of functions taking a parameter of type a and evaluating to a result of type b.) Notably, an applied type must have a specific named type function as its root; you can't have m Int, which you would need for generalised monads.
Type constants and applied types are monotypes. You get a polytype by optionally sticking one or more "∀"s in front of a monotype. ("∀" is pronounced "for all", and in Haskell can be written forall.) So for example a -> Int is a monotype, but ∀a. a -> Int is a polytype. So is ∀a. ∀b. a -> Int -> b, which is written equivalently as ∀a b. a -> Int -> b. ∀b. a -> Int is also a polytype; since the quantified variable doesn't show up, it's equivalent to the monotype a -> Int. We can do something like that to any monotype, so for simplicity we might as well decide that monotypes count as a special case of polytypes, not as a distinct set.
Type signatures in Elm typically have an implied "∀" over whichever variables it makes sense to quantify. (There's no syntax for explicitly writing the "∀".) So the type of List.map would be written
map : (a -> b) -> List a -> List b
but I'll be writing
map : ∀a b. (a -> b) -> List a -> List b
for clarity. Because there's one place where Elm doesn't give an implied ∀, which is when you have scoped types. To demonstrate by example,
const : ∀a b. a -> b -> a
const x = let foo : b -> a
foo y = x
in foo
const has a polytype here, but foo has a monotype, because (in context) its argument type and return type are constrained. If you tried to swap a and b in the type signature for foo, or rename either of them, the Elm compiler would complain.
Language
The language has four kinds of expression, and each has a rule relating it to the type system. You need variables and constants, function calls, lambda expressions, and let statements.
Variables and constants
Variables and constants are things like True, 0.2, Just, "Hello", [], (), List.map. Each of these has a declared type, which in Elm is notated with :. So True : Bool, 0.2 : Float, Just : ∀a. a -> Maybe a, "Hello": String, [] : ∀a. List a, () : (), List.map : ∀a b. (a -> b) -> List a -> List b.
The rule that relates these to the type system is that type declarations imply type judgments. Mathematically it looks like
$$ \frac{x : π \quad π ⊑ μ}{x \sim μ}. $$
Reading clockwise from top left, this says: if you have a variable $x$ declared to have some polytype $π$, and if the monotype $μ$ is a specialisation of $π$, then $x$ can be judged to have type $μ$. ($π$ always denotes a polytype, and $μ$ always denotes a monotype.)
A type judgment, as opposed to a declaration, provides a type that an expression can be used as. A judgment is always as a monotype.
And type specialisation, denoted $⊑$, is the process of replacing quantified variables with less-quantified ones. So for example the type ∀a b. a -> b -> a might be specialized to ∀a. a -> String -> a, or to ∀b. Int -> b -> Int; and from either of those, it could be further specialised to Int -> String -> Int. Of course String -> Int -> String and List Float -> (Float -> String) -> List Float are valid specialisations too.
Thus: we have the type declaration [] : ∀a. List a, and we have (∀a. List a) ⊑ List Int, and so we can form the type judgment [] ~ List Int. We also have (∀a. List a) ⊑ List String, and so [] ~ List String. And [] ~ List (List (Maybe Bool)), and so on.
Function calls
Function calls are things like not True, (+ 1), List.Map Just. And the rule relating them to the type system is that function calls consume function types. This is the simplest of the rules. Mathematically it looks like
$$ \frac{f \sim μ → μ' \quad v \sim μ}{f v \sim μ'}. $$
Or: if $f$ can be judged to have a function type $μ → μ'$, and $v$ can be judged to have type $μ$, then the function call $fv$ can be judged to have type $μ'$.
Thus: we can infer the type judgment toString ~ (Int -> String), and we can infer 3 ~ Int, and so we can infer toString 3 ~ String.
Also, we can infer List.map ~ ((Int -> Maybe Int) -> (List Int -> List (Maybe Int))), and we can infer Just ~ (Int -> Maybe Int). So we can infer List.map Just ~ (List Int -> List (Maybe Int))
Lambda expressions
Lambda expressions are things like \x -> Just x, and in Elm they're used implicitly when something like const x y = x is turned into const = \x -> \y -> x. The type system rule is that lambda expressions produce function types. Mathematically:
$$ \frac{x : μ ⇒ e \sim μ'}{λx.e \sim μ → μ'}. $$
Or: suppose that the type declaration $x : μ$ would allow us to infer the judgment $e \sim μ'$. In that case, we could judge that $λx.e \sim (μ → μ)'$.
Typically $e$ would be some expression mentioning the variable $x$, but it's no problem if not. In that case, if you can get $e \sim μ'$ at all, you can get it assuming any $x : μ$, and so you have $λx.e \sim (\mathtt{Int} → μ')$ and $λx.e \sim (\mathtt{String} → μ')$ and $λx.e \sim (\mathtt{Result\ String\ (List\ (Maybe\ Float))} → μ')$ and so on.
Thus: given the declaration x : Int, we can infer the judgment [x] ~ List Int. And so we can infer the judgment (\x -> [x]) ~ (Int -> List Int).
Let expressions
Let expressions read like let x = y in a. Semantically, this is very similar to using a lambda expression, (\x -> a) y. But HM treats them differently in the type system, allowing a let expression to introduce polytypes. That permits code like
let f x = [x]
in (f "", f True)
-- returns ([""], [True])
If you tried to rewrite this as a lambda, you would get
(\f -> (f "", f True))(\x -> [x])
But type inference fails here, because there's no monotype declaration for f that allows a type judgment for (f "", f True). So the precondition for the lambda rule never obtains, and so in turn, no type judgment can be made for the expression \f -> (f "", f True).
Let expressions compensate for this deficiency, with the rule let expressions are like polymorphic lambda applications. (I don't have a good name for it.) Mathematically:
$$ \frac{a \sim μ \quad x : \bar{μ} ⇒ b \sim μ'}
{(\mathtt{let}\ x = a\ \mathtt{in}\ b) \sim μ'} $$
Or: suppose that $a$ can be judged to have type $μ$, and that the declaration $x : \bar{μ}$ would allow us to infer the judgment $b \sim μ'$. In that case, we could judge that $(\mathtt{let}\ x = a\ \mathtt{in}\ b)$ has type $μ'$.
This introduces the notation $\bar{μ}$, which generalises a monotype to a polytype. How it works is: if $μ$ mentions a type variable $a$, and $a$ isn't quantified over in the surrounding context, then $\bar{μ}$ contains a "$∀a$".
Thus: we can infer (\x -> [x]) ~ (a -> List a), where a is a type variable unused in the surrounding context. That type generalises to ∀a. a -> List a. And given the declaration f : ∀a. a -> List a, we can infer (f "", f True) ~ (List String, List Bool). So in total, we can infer
$$ (\mathtt{let\ f\ x\ =\ [x]\ in\ (f\ "",\ f\ True)})
\sim \mathtt{(List\ String,\ List\ Bool)}. $$
(It seems a little strange to me that the approach here is to first construct a meaningless type, and then quantify over it. Still, that's my understanding. It's of course possible I'm mistaken.)
Why do we need both let and lambda? Well, we can't replace lambda expressions with let expressions: they're not re-usable. (When you translate a let expression into a lambda expression, you actually generate a lambda applied to an argument. There's no way to translate a lambda expression by itself into a let expression.) Meanwhile, I'm not entirely sure why we can't make lambdas polymorphic in the same way let expressions are. I think the answer is that if we tried it, we'd lose some of the legibility that HM offers - so let can be more powerful in the type system because it's less powerful in the language. But I'm not sure exactly what legibility would be lost.
Recursion
There's an interesting thing about the system I just described: it may or may not be Turing complete.
The problem is that there's no specified way of doing recursion. A function can't call itself, and it can't call any other function that can call it.
But a fixed-point combinator allows recursion, and might be included in the initial set of variables. Failing that, the proper recursive types can be used to define one. (Elm and Haskell allow us to define such types.)
Failing both of those, we can introduce a new kind of expression
$$ \frac{x : μ ⇒ a \sim μ \quad x : \bar{μ} ⇒ b \sim μ'}
{(\mathtt{letrec}\ x = a\ \mathtt{in}\ b) \sim μ'}. $$
This is much the same as let, but makes the variable x = a available when evaluating a. It's only available as a monotype when evaluating a, and still doesn't get generalised to a polytype until evaluating b.
(Elm and Haskell provide letrec as let and don't provide simple let at all.)
But if an HM language doesn't provide the appropriate variables or types, and doesn't implement letrec or something similar, it won't be Turing complete. Legibility gain, expressivity cost.
Wrapping up
And modulo some small details, that's the entirety of a Hindley-Milner type system. If you have a language with those features, and a suitable set of types, you can perform type inference.
What we have is a set of rules that allows us to construct proofs. That is, if we look at a program written in this language, we would be able to construct a proof of its type (or lack thereof). But I already said HM is better than that: it lets us mechanically construct a proof, in (roughly) linear time.
I confess, I'm not entirely sure how to do that. The outline is obvious, recurse down the parse tree and at each step apply the appropriate rule. But since a constant can be judged as one of many types, you need to keep track of which types are acceptable. Wikipedia hints at how it works, but not in a way that I understand particularly well.
Elm and Haskell both support many things not covered so far. To look at some of them briefly, and occasionally getting even more recklesss,
-
It seems obvious, but both allow you to evaluate the language, something I haven't touched on much. And it does need to be touched on, because there's more than one way to do it. Haskell uses a lazy evaluation model, while Elm is strict.
-
Both have ways to introduce new types. That doesn't change what we've seen, but it does separate the languages into two parts. One part describes the types used in a program and one part implements the semantics of a program.
-
Both also support case statements along with destructuring, like
mHead : Maybe (List a) -> Result Bool a
mHead ml = case ml of
Just (a::_) -> Ok a
Just _ -> Err True
Nothing -> Err False
To implement these, you'd want to add a fifth class of language expression. But I think it would be possible in theory to write a "thin" first-pass compiler to translate these statements into the existing language. By "thin" I mean to do this in such a way that we don't lose any of the legibility guarantees we care about. (For example, if this compiler turned $n$ bytes of code in a case statement into more than $O(n)$ bytes of code in the base language, or if it ran in more than O(n) time, this condition would fail.)
If I'm right about that, then case statements neither make the language more expressive nor less legible, at least in one important sense.
-
(By comparison, if-then-else statements are also another class of language expression, but one which can obviously be thinly compiled down to the existing ones.)
-
In the type system, Elm supports record types, which are a lot like tuples but with nicer syntax. I believe these too could be thinly compiled down. But it also supports extensible records, which are more complicated. On one level you can think of a type like {a | x : Int, y : Int} like a tuple ∀a. (a, Int, Int). But then this tuple needs to be unpacked and manipulated when you pass it into a function expecting an {a | x : Int}.
I believe this is unresolvable, and extensible records represent an extension of Elm from HM. (But one with fairly minor legibility costs, in comparison to the expressiveness gains.)
-
Haskell supports typeclasses, which are a way of allowing functions to operate on multiple different types. (For example, the show function can be applied to a String, an Int, a (), a [Float], ….) Elm doesn't, but simple typeclasses can be emulated with only a little added verbosity.
Another thing I'll say is that I've been talking about legibility and expressivity of a language. But a type system is itself a language, and may be more or less legible and expressive. I don't have a strong intuition for how these interact.
There's a lot more I could add to this post. Some things that I omitted for brevity, some that I omitted because I don't know enough about them yet, and some that I omitted because I don't know about them at all. I don't know what a sensible cutoff point is, so I'm just going to end it here.
From writing my original talk, and subsequently this blog post, I think I understand HM type systems much better than I used to. Hopefully you think the same. Hopefully we're both correct. If you see any inaccuracies, please point them out.
Posted on 05 May 2019
|
Comments
Related: be nice, at least until you can coordinate meanness.
A premise of this post is that punching people is sometimes better than the alternatives.
I mean that literally, but mostly metaphorically. Things I take as metaphorical punching include name calling, writing angry tweets to or about someone, ejecting them from a group, callout posts, and arguing that we should punch them.
Given that punching people is sometimes better than the alternatives, I think we need to be able to have conversations about when "sometimes" is. And indeed we can and do have those conversations. Many words have been spilled on the subject.
But I think it's probably a good idea to try to avoid having those conversations while actually punching people.
Here's what I mean. Alice thinks that punching Bob is better than the alternatives. But she thinks that if she just starts punching, Carol and Dave and Eve might not understand why. Not even if she tells them what Bob has done. She thinks punching Bob is better than the alternives, but she thinks the reasons for that are slightly complicated and haven't previously been articulated very well, at least not in a way that makes them common knowledge.
So she writes an essay in which:
-
She proposes a theory for when punching people is better than the alternatives. (She readily admits that the theory is not complete, nor is it intended to be, but it covers part of the space.)
-
She describes the situation with Bob, and how the theory justifies punching him.
-
She punches Bob.
I think this could be a mistake. I think she should maybe split that post into at least two parts, published separately. In the first part, she proposes the theory with no mention of Bob. Then, if Carol and Dave and Eve seem to more-or-less agree with the theory, she can also publish the part where it relates to Bob, and punch him.
I think this has a few advantages.
-
Suppose Alice can't convince anyone that the theory holds. Then Bob is kept out of things entirely, unless Alice wants to go ahead and punch him even knowing that people won't join in. In that case, people know in advance that Alice is punching under a theory that isn't commonly subscribed to.
-
Suppose the theory is sound, and also justifies punching Fred. Then someone can link to the theory post separately, without implicitly bringing up the whole Bob thing. This is especially good if the theory doesn't actually justify punching Bob, but it's somewhat good regardless.
-
Suppose Bob disagrees with some part of the argument. When he gets punched, he's likely to be triggered or at least defensive. That's going to make it harder for him to articulate his disagreement. If it comes split up, the "thing he has to react to while triggered" may be smaller. (It may not be, if he has to react to the whole thing; but even then, he may have seen the first article, and had a chance to respond to it, before getting punched.)
-
Suppose that splitting-things-up like this becomes a community norm. Now, if Alice just wants to come up with excuses to punch Bob, it's harder for her to do that and get away with it, harder for her to make it look like an honest mistake.
It might seem even better to split into three posts: theory, then application ("and here's why that justifies punching Bob"), and then wait for another post to actually punch him. But since "arguing that we should punch Bob" is a form of punching Bob, splitting those two out isn't necessarily possible. At best it would be "theory, then application and mild punching, then full-strength punching". It's more likely to be worth it if there's a big difference between the two levels. "Here is why I think I should kick Bob out of the group" is considerably weaker than "I hereby kick Bob out of the group". But "here is why I think you all should stop trusting Bob now" is not much weaker than "you all should stop trusting Bob now".
However, I don't think this is always unambiguously a good thing. There are some disadvantages too:
- The initial post is likely to be drier, less compelling, without concrete examples. And perhaps harder to evaluate, especially for less abstract thinkers.
-
You can't really remove the initial post from its context of "Alice thinks we should punch Bob". You can hide that context, but that doesn't remove its influence. For example, if there are cases similar to Bob's that would be covered by the same theory, Alice's post is likely to gloss over the parts of the theory that relate to them-but-not-Bob, and to focus too much on the parts that relate to Bob-but-not-them.
-
Suppose the theory is sound, but the facts of the case don't support punching Bob. Splitting the posts adds more opportunity for sleight-of-hand, such as using a term to mean different things in different places. This would be harder to notice in a split post than a monolithic post, if each part is internally consistent.
-
It may be harder to write this way, which may cause some better-than-the-alternatives punching to go unperformed.
-
It's slower. Sometimes that's probably neutral-to-good. But often, if punching someone is better than the alternatives, it's because they're currently hurting other people. If punching them will make them stop, then ideally we want to punch quickly.
I'm not sure how all these factors really shake out, and I expect it'll vary from case to case. So I don't want to offer a blanket suggestion. I think my advice is: if you're thinking of writing one of those all-in-one posts, consider splitting it up. It won't always be the right thing to do, but I think it's an option to bear in mind. Here are some questions to ask that might sway you in one direction or the other:
- How hard are you punching? If someone googles Bob, will they find your punches? (At least once, Scott Alexander used a pseudonym for a person he was punching; this seems like a useful tool.)
-
If the punching is delayed, does anything bad happen?
-
Does the theory apply more generally than it needs to for this specific case? Thinking of similar cases might help, especially real ones but also fictional. (If you can think of lots of real cases, the value of having a reference post for the theory goes up, and its value as a reference post goes up if it has less baggage.)
(As an aside: I want to note that a post which looks like an all-in-one might not be. It may be recapping previously established theory. Common knowledge is rarely absolutely common, so I suspect this will usually be a good idea.)
Posted on 16 October 2018
|
Comments
I've been doing a little bit of matched betting lately. The idea is that you place two opposite bets on the same event, calibrated so that your profit will be the same no matter which bet wins. If you do this entirely with your own money, your profit will (under reasonable assumptions) be negative. But bookmakers often offer free bets; you can use matched betting to extract most of the amount of that free bet as actual money.
This post isn't advice about how to get into matched betting. That market is probably saturated; if you want to learn, I used this guide and it served me well. (However, if anyone is inspired to try it by this post, I have a referral code for smarkets: safto14. It looks like if you sign up with that and bet $£20$, both you and I will receive $£10$ in risk-free bets. I swear that's not why I'm posting this. I might not even get around to using it.)
(Um, but after that I feel obliged to give at least some safety information. So here goes: if you're not a UK citizen currently in the UK, this may be a bad idea. Don't use credit cards to deposit funds; it seems they interpret that as a cash transaction and charge fees. Start small; that way there's less at risk in case you do something silly like use a credit card to deposit funds. Probably don't expect to earn lots of money this way, either in total or per-hour.)
Instead, I want to go into the math behind it, in more depth than I've seen in other places. None of this math is complicated, but some of it is useful, and I haven't found it anywhere else. (I even deliberately went looking.)
A simple example
(If you've seen one example of matched betting, you've seen them all, and you can skip this particular one.)
You have a $£10$ free bet at a bookmaker. You find a football game, say Manchester Utd versus Liverpool, that you want to bet on. The bookmaker offers odds of $4$ on Liverpool, and you bet your $£10$ on them.
(A note on odds: the usual convention in gambling seems to be to use decimal odds. Odds of $x$ mean that your potential winnings are $x-1$ times your stake. Thus, odds of $4$ mean a bet of $£10$ has the potential to pay out $£30$. If you're used to odds notated $a:b$ or (equivalently) $a/b$, then the decimal odds are given by $a/b + 1$.)
So if Liverpool wins, you'll earn $£30$; if they lose or draw, you lose nothing. You then look up the same match at a betting exchange. An exchange allows you to take both sides of a bet, which a bookmaker won't. The exchange offers odds of $4.3$ to lay Liverpool; this means that you win your bet in the exchange only if Liverpool doesn't win. You accept a stake of $£6.98$, which means your own stake is $£23.03$.
Now if Liverpool wins the match, the bookmaker pays you $£30$ and you lose $£23.03$ in the exchange, for a net profit of $£6.97$. And if Liverpool loses, you earn $£6.98$ in the exchange and lose nothing at the bookmaker, for a net profit of $£6.98$. You've turned a $£10$ free bet into almost $£7$ of actual money.
(I'm ignoring for now the commission that the exchange will usually collect when you win a bet on them. With $2\%$ commission, you would instead accept stakes of $£7.01$, wagering your own $£23.13$; if Liverpool doesn't win, you would earn $£7.01 · 0.98 = £6.87$, which is also what you'd earn if Liverpool does win.)
Before bookmakers will give you a free bet, you'll usually have to place a bet with them using your own money. You lose a small amount of money on this bet, but you can use the same principles to ensure that you lose the same amount no matter who wins. You might lose around $£0.50$ on a $£10$ qualifying bet, in which case you end up with around $£6.50$ profit when all's said and done.
This has been a very brief introduction to matched betting. Now, into the math. I'm going to be focusing on two kinds of bet: qualifying bets, which are usually known as just bets, and free bets, where you don't lose anything if your back bet loses. I'm also going to ignore rounding; let's just pretend that the sterling is infinitely divisible.
Some definitions
We can think of a paired bet as having six parameters, $(O_b, O_l, S_b, S_l, C_b, C_l)$. These are three parameters for each of a pair of back and lay bets.
$O_b, O_l ≥ 1$ are the odds on the back and lay bets. It's typically safe to assume $O_b < O_l$; otherwise, modulo commission, you could make a profit even on your qualifying bets. They can't be less than $1$ because we're using decimal odds; that would correspond to a probability below $0$.
$S_b, S_l ≥ 0$ are the stakes on the back and lay bets. Note that $S_l$ is the stake offered by the other party to your lay bet; it's (roughly) the amount you stand to win on that bet, not the amount you stand to lose. This may seem strange, but it's the convention used.
And $C_b, C_l ∈ [0, 1]$ are the commission charged on your winnings on each side. Usually $C_b = 0$: bookmakers don't charge commissions, they make money by offering low odds. The two exchanges I've used have $C_l = 2\% = 0.02$ (Smarkets) and $C_l = 5\% = 0.05$ (Betfair).
I'm also going to introduce the symbol $C^+ = (1 - C_l)(1 - C_b)$. If you passed $£1$ through your bookmaker and exchange, and they each charged commission and nothing else, you would have $£C^+$ left at the end. $C^+$ isn't enough for us to fully understand a matched bet, we need the individual back and lay commissions as well, but it'll be convenient shorthand.
Now let $R_{xy}$ (where $x,y ∈ \{b,l\}$) be your return on side $y$ if your bet on side $x$ wins. So for a qualifying bet (which is just a regular bet, outside the context of matched betting), we have:
$$ \begin{align*}
R_{bb} &= S_b (O_b - 1) (1 - C_b) \\
R_{bl} &= - S_l (O_l - 1) \\
R_{lb} &= - S_b \\
R_{ll} &= S_l (1 - C_l).
\end{align*} $$
For a free bet, the only change is
So your profit is $R_{bb} + R_{bl}$ if your back bet wins; and $R_{lb} + R_{ll}$ if your lay bet wins.
And now we can say that a matched bet is simply a paired bet, where your profit is the same in either case. I won't need to talk about simple paired bets from now on; all bets are matched. When I talk about a "free bet" or "qualifying bet", those are matched bets too.
Incidentally, the six prameters are over-determined. Most commonly we want to learn $S_l$ given the other five; but knowing any five of them will fix the value of the sixth.
Optimal lay stake
The first question we'll ask is, given $O_*$, $C_*$ and $S_b$, what must $S_l$ be to make our bet a matched bet? Or in other words, what $S_l$ should we choose to eliminate all risk?
We need
$$ R_{bb} + R_{bl} = R_{lb} + R_{ll} $$
which after some (perhaps silly-seeming) substitution and rearrangement gives
$$ S_l = { R_{bb} - R_{lb} \over R_{ll}/S_l - R_{bl}/S_l }. $$
This looks circular, but when we substitute for the values of $R_{**}$, $S_l$ disappears from the right hand side. For a qualifying bet, this gives
$$ S_l = S_b { (O_b - 1)(1 - C_b) + 1 \over O_l - C_l }, $$
and for a free bet,
$$ S_l = S_b { (O_b - 1)(1 - C_b) \over O_l - C_l }. $$
A thing to note here is that $O_l$ and $C_l$ only appear in the term $O_l - C_l$. In other words, the effect of lay commission is to decrease the effective lay odds in the most natural way. It would be nice if this happened in other contexts too, but unfortunately I haven't come across it. The $O_l - C_l$ term is common, but it's usually accompanied by another $O_l$ and/or $C_l$ somewhere else in the expression.
Profit
Next, we'll want to know how much profit we make. This is given by $R_{lb} + R_{ll}$, where we calculate $R_{ll}$ using the lay stake we just found. But since both of these terms are proportional to $S_b$, we'll find it more convenient to think in terms of profit per unit of back stake,
$$ P = { R_{lb} + R_{ll} \over S_b }. $$
Under a qualifying bet, this is
$$ P_q = C^+ { O_b + C_b/(1 - C_b) \over O_l - C_l } - 1, $$
and for a free bet, it's
$$ P_f = C^+ { O_b - 1 \over O_l - C_l }. $$
We can look at these functions graphically:
(all images link to larger versions)
each line represents a contour of the function, a set of points that all have the same profit. The sets of contours look superficially similar, but they're generally steeper for a free bet, and they get cut off on the bottom edge instead of the left edge. In both cases, profit increases with $O_b$ and decreases with $O_l$.
We can reparameterise in terms of $O_b$ and $σ = O_l - O_b$, the spread between the back and lay odds. Since $O_l ≥ O_b$, we only need to consider $σ ≥ 0$. This gives us
$$ \begin{align*}
P_q &= C^+ { O_b + C_b/(1 - C_b) \over O_b + σ - C_l } - 1 \\
P_f &= C^+ { O_b - 1 \over O_b + σ - C_l }.
\end{align*} $$
These are slightly more distinct. Looking at these graphs, it seems that for a qualifying bet, having low $σ$ is more significant than having high $O_b$; but for a free bet, having high $O_b$ is more significant than having low $σ$. If so, that suggests you might want to be looking for different sorts of bets at each stage. (It is so, and we'll make it more precise later.)
We can also look at $P_f - P_q$, the difference in profit between a qualifying bet and a free bet. This isn't particularly useful to compare bets: you place qualifying bets to get free bets, and you place free bets to get money, and if you're doing pure matched betting, I don't think you'll ever be asking yourself should I place this bet free or as a qualifier? Still, the difference is
$$ P_f - P_q = 1 - { (1 - C_l)(1 - 2C_b) \over O_l - C_l }. $$
The more $O_l$ grows, the worse a qualifier becomes relative to a free bet. This is another suggestion that you should be looking at different sorts of bets for your qualifiers and your free bets.
Liability
One more thing is important when making a matched bet: lay liability. This is how much you stand to lose on the exchange where you make your lay bet. (It's only important for boring real-world reasons like liquidity and the possibility of doing something stupid, but those are still important.) You need to have this much money in your account at the exchange, which means you need to be able to spare it from your bank account for a week or so. Low-liability bets are also safer if something goes wrong, which makes them a good choice for early dabblers in matched betting.
Liability is simply given by $-R_{bl} = S_l (O_l - 1)$, which is
$$ S_b (O_l - 1) { (O_b - 1)(1 - C_b) + 1 \over O_l - C_l } $$
for a qualifying bet and
$$ S_b (O_l - 1) { (O_b - 1)(1 - C_b) \over O_l - C_l } $$
for a free bet.
(I made the graphs in $σ$ as well, but they're too boring to include inline)
Unlike profit, liability increases with both $O_b$ and $O_l$. But it increases arbitrarily with $O_b$, and asymtotically with $O_l$; it's bounded above by roughly $S_b O_b$ for a qualifying bet and $S_b (O_b - 1)$ for a free bet. (If the graphs were extended further, as they stretch upwards the lines would become ever more vertical, but they'd always stay separate. To the right, the lines would become ever more horizontal, all of them converging on $O_l = 1$.)
Improving on a free bet
Matched bet calculators aren't hard to find, and what I've given so far is nothing that they can't do for you. But they don't tell you everything you might want to know. Let's look at a bet, and see how we might find a better bet. Since the two types have different behaviours, we'll treat them separately.
To maximise profit, we usually need to consider that $S_b, C_b$ and $C_l$ are fixed, and find the dependence of $P$ on $O_b$ and $O_l$. For a free bet, that means we want to maximise the term
$$ P_f ∝ {O_b - 1 \over O_l - C_l}. $$
This tells us a few things. The first is that we want high back odds and low lay odds. We already knew that, and it's not very helpful; we expect back and lay odds to more-or-less rise and fall together. It also tells us that adding a constant to both odds will increase profit; odds of 5 and 6 will be better than odds of 4 and 5. (This, too, we could have deduced before; or we could have seen it on the graph of $P_f(O_b, σ)$.)
But consider what happens when $σ = 0$. Then the term in question is
$$ { O_b - 1 \over O_b - C_l } $$
which, as $O_b$ ranges from $1$ to $∞$, takes all values in $[0, 1)$. But when $σ > 0$, the possible values are exactly the same; high $σ$ changes the $O_b$ that gives you any particular profit, but it doesn't make any profit value available or unavailable.
What that means is: given any free bet, we can construct another free bet with equal profit but $σ = 0$, not changing $S_b$ or $C_*$.
Or: given odds $O_b, O_l$, we can calulate the odds $O'$ that would give you the same profit, if you could find these odds for both a back and a lay bet.
In turn, that tells you that if you want to improve your profits, you can ignore bets with $O_b < O'$. (Because for those bets, $P_f(O_b, σ) < P_f(O', σ) ≤ P_f(O', 0)$. The first inequality comes from adding a constant to both odds, and the second comes from reducing $O_l$.) This is a useful thing to know, that matched bet calculators don't tell you.
To find $O'$, we set
$$ { O_b - 1 \over O_l - C_l } = { O' - 1 \over O' - C_l } $$
and deduce
$$ \begin{align*}
O' &= { O_l - O_bC_l \over 1 + O_l - O_b - C_l } \\
&= O_b { 1 - C_l + σ/O_b \over 1 - C_l + σ }.
\end{align*} $$
The expression with $σ$ isn't exactly simpler, but I think it's more aesthetically pleasing. (Consider that $1-C_l$ is approximately as fundamental as $C_l$ itself.) Graphically:
We can also calculate $O'$ simply as a function of profit, and vice versa:
$$ P_f = C^+ { O' - 1 \over O' - C_l } \\
O' = { C_lP_f - C^+ \over P_f - C^+ } $$
$P_f$ approaches an asymtote at $C^+$, but slowly. With $C_b = 0, C_l = 0.02$, extracting $80\%$ of a free bet is only possible if $O_b ≥ 5.36$. For $90\%$, you need $O_b ≥ 12.03$. Such bets are somewhat rare in my experience, and typically have high spread.
We can go more general. Given a profit, we can calculate the level curve of all bets which generate that profit; the case $σ=0$ gives us only a single point on that curve. The curve divides bet-space into two regions, so that it's easy to see whether a bet gives more or less than this amount of profit.
(Earlier we saw this level curve graphically, for certain specific profits. Now we find the explicit formula for the curve, which I secretly already used to draw the graphs.)
We already have
$$ \begin{align*}
P_f &= C^+ { O_b - 1 \over O_l - C_l } \\
&= C^+ { O_b - 1 \over O_b + σ - C_l },
\end{align*} $$
and it's just a matter of rearranging these:
$$ O_b C^+ = P_f (O_l - C_l) + C^+\\
O_b (C^+ - P_f) = P_f (σ - C_l) + C^+. $$
These two equations can be used to find $O_b$ in terms of $O_l$ or $σ$, and vice-versa. Both are very simple at heart: they're linear relationships, that could be rearranged to the form $y = mx + c$.
Looking more closely at the second one, notice that $C^+$ is the upper bound on profit. So the term $C^+ - P_f$ can be thought of as how much profit is being left on the table, compared to what you could hypothetically get if odds of $∞$ were a thing. The less profit you leave behind, the less $σ$ has to change to compensate for a given change in $O_b$. In other words, when profit is high, the level curve on the graph of $P_f(O_b, σ)$ becomes shallower, as we saw above.
Improving on a qualifying bet
For a qualifying bet, we can't quite do the same thing. If we temporarily assume $C_b = 0$, then the term we want to maximise is
$$ P_q + 1 ∝ {O_b \over O_l - C_l}. $$
This doesn't work the same as the equivalent term for a free bet. If you keep $σ$ fixed and consider profit as a function of $O_b$, then this function acts differently depending on the sign of $σ - C_l$. If $σ ≤ C_l$, then regardless of $O_b$ you get more profit than is ever possible with $σ > C_l$.
This isn't immediately practically important, because $σ > C_l$ is a pretty safe assumption. But it's mathematically significant. For a free bet, setting $σ$ to $0$ doesn't rule out any profit levels, so we could ask "how would we get this particular profit with $σ = 0$?" If we try to ask that for a qualifying bet, the answer is typically that we can't. So the approach we used for a free bet doesn't work on a qualifying bet.
We also can't set $O_b$ to its best possible value, because it can go arbitrarily high. But we can try setting it to its limiting worst value ($O_b = 1$). We find $σ'$ such that
$$ { O_b + C_b/(1 - C_b) \over O_b + σ - C_l }
= { 1 + C_b/(1 - C_b) \over 1 + σ' - C_l }, $$
which gives us
$$ σ' = { σ + (O_b - 1)(1 - C^+) \over 1 + (O_b - 1)(1 - C_b) }. $$
Now we know that any bet with a spread less than $σ'$ will give better profit than the bet we started with. Unfortunately, I think this still isn't as good as what we got for a free bet, for three reasons.
-
For a free bet, we had an easy negative test: some bets (those with $O_b < O'$) could be ruled out on a glance, but verifying them took more work. Here, the test is positive: some bets (those with $σ < σ'$) can be accepted on a glance, but verifying the others takes more work.
In practice, I expect the positive test will almost alway be inconclusive, meaning you still need to do the more difficult check on every bet. (I haven't done enough betting myself, while writing this, to say from experience.)
-
My workflow is to find a plausible-looking back bet and then see how it would be matched. With a free bet, I can run the easy test without looking for the match. For a qualifying bet, I need to find both sides of the bet before I can run the easy test.
-
Qualifying bets often must be placed at a minimum odds (on the back side) in order to count. That typically rules out the lowest-spread bets (see below digression).
Still, this is what we have. Following a similar theme as before, we can calculate $σ'$ and $P_q$ as functions of each other:
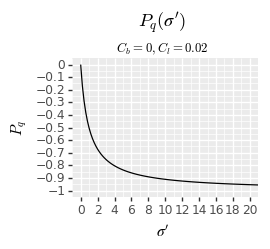
$$ P_q = { 1 - C_l \over 1 - C_l + σ' } - 1 \\
σ' = { 1 - C_l \over P_q + 1 } + C_l - 1. $$
(Note that these equations don't contain $C_b$. That's not because we're assuming it's $0$: when you set $O_b = 1$, $C_b$ completely disappears from the equation for $P_q$.)
Interestingly, the bounds of $P_q$ don't depend on commission at all. As $σ'$ grows, $P_q$ always approaches an asymtote at $-1$, which isn't surprising: you can't quite lose your entire back stake, but you can get arbitrarily close to that, even with no commission.
On the other edge of the graph, we always have $P_q(O_b=1, σ'=0) = 0$. (That may not be clear on this image, but it's easy to see algrebraically.) That's because at $O_b = O_l = 1$, both bets are completely one-sided. On the back side you have a chance of losing money, but no way to win it; on the lay side you have a chance of winning money, but no way to lose it. In particular, if the back bet wins, you make no profit or loss on either bet, so commission is irrelevant. And so the lay stake is calibrated for your lay winnings, after commission, to cancel out your back loss. (But if someone is willing to give you free maybe-money, you might as well ask for as much maybe-money as they're willing to give you.)
And again, given profit, we can calculate the level curve of bets which return that profit. Unsurprisingly, we find another linear relationship; it comes to
$$ O_bC^+ + C_b(1 - C_l) = (Pq + 1)(Ol - Cl) \\
O_b(1 - C_b - Λ) + C_b = Λ(σ - C_l), $$
where
$$ Λ = { P_q + 1 \over 1 - C_l }. $$
I'm afraid I can offer no particular interpretation of what $Λ$ means, though I observe that we can substitute it into a previous equation, $σ' = 1/Λ + C_l - 1$. Note that if $Λ ≥ 1 - C_b$, equivalently if $P_q + 1 ≥ C^+$, then $σ$ and $O_b$ start to move in opposite directions: for fixed profit, $σ$ goes up as $O_b$ goes down. At this point, you get more profit with low $O_b$ as well as with low $σ$, which would be convenient if it was ever realistically going to happen.
(It turns out that $P_q + 1 ≥ C^+$ precisely when $σ ≤ C_l + C_b/(1 - C_b)$. I noted above that if $C_b = 0$, the possible values of $P_q + 1$ depend on the sign of $σ-C_l$. This is the same result, generalized to all values of $C_b$.)
A digression on odds
Note that in general, you can expect spread to be lower at lower odds. That's because odds are more sensitive to evidence when they're high than when they're low.
There's a technical interpretation of that, but I'm just going to illustrate by example. Consider the probabilities $1/5$ and $1/6$. These are complementary to $4/5$ and $5/6$ - the two pairs of probabilities encode the same information. Converting to decimal, probabilities $1/5$ and $1/6$ are decimal odds $1.25$ and $1.2$; and probabilities $4/5$ and $5/6$ are decimal odds $5$ and $6$.
So the difference between the odds $1.25$ and $1.2$ is, in a very important sense, the same as the difference between $5$ and $6$. But when it comes to betting, the spreads of $0.05$ and $1$ are very different.
The takeaway from this is that for qualifying bets, you should be looking at bets with low odds. High odds have better returns, but the effect of low spread is much more significant, and low spread comes with low odds.
The effects of commission
I want to explore one more question: how does profit depend on commission? For this, we'll keep $C_b$ and $O_b$ fixed, and explore how $O_l$ and $C_l$ affect profit.
Conveniently, the term we want to maximise is the same,
$$ \begin{align*}
P_q + 1 ∝ { 1 - C_l \over O_l - C_l } \\
P_f ∝ { 1 - C_l \over O_l - C_l }.
\end{align*} $$
So if we find the same lay bet on two different exchanges, we can compare them without regard for the back bet we'd be matching.
The two exchanges I've used have $C_l$ of $0.02$ and $0.05$, so they give equal profits when
$$ { 0.98 \over O_S - 0.02 } = { 0.95 \over O_B - 0.95 } $$
where $O_S$ is the odds offered on Smarkets and $O_B$ is the odds offered on Betfair. This rearranges to
Since $98/95 ≈ 1.03$, it's better to use Betfair than Smarkets if the offered odds are roughly $3%$ lower, which happens to be the difference in commission. So for example, odds of $6$ on Betfair correspond to roughly $6.19$ on Smarkets.
It should be easy to take a bunch of equivalent bets on the two sites, and compare to see which seems likely to give better profit in general. I started doing that, but then I looked at three football games and got bored and stopped.
They all had exactly the same odds on all three positions (win/draw/win), even when they fluctuated slightly pre-game. (I did look at one game as it began, and the two sites didn't quite stay in sync then. But betting while odds are fluctuating a lot is a bad idea.) This suggests that Smarkets typically offers better profits. But Betfair is a more popular site, which probably has advantages; in particular, it's plausible that a large bet would be harder to fully match on Smarkets.
And that's it. There are plenty more interesting questions you could ask, but I'm going to stop there.
Something that would be nice would be a calculator that can make use of this. The online calculators all seem pretty crap: they only tell you profit, lay stake and lay liability, and only for one bet at a time. Being able to compare bets seems like it would be a pretty important feature, but I haven't seen it anywhere. (Some of them have features to work with more complicated types of bets than I've looked at, but I don't care about that. Here's one that's no worse than any other.) I've also seen an excel calculator, which had the neat feature of automatically adding bets to a spreadsheet. But again, only one bet at a time; plus, I don't have excel, and don't keep track of my bets in a spreadsheet. (I use ledger, though it's not a great fit.)
I've written a command-line tool that can show you multiple bets at a time for comparison purposes. It also shows you, for a free bet, the lowest possible back odds to improve on your highest-profit bet ($O'$); or, for a qualifying bet, the highest possible spread that won't improve on it ($σ'$).
But the interface isn't very good, I think partly because of the limits of the command line and partly because of a questionable design decision (see the README). And it can't show graphs, which I think would be nice. If you want to use it anyway, it's on github.
If I were to dedicate more time to the project, I currently think I'd start again in Javascript. I think I have a vague idea of how a decent one could work. But right now, as far as I can tell there are no good calculators.
Posted on 02 June 2018
|
Comments
this is surely not an original insight, but I haven't seen it before
A Pareto improvement is where you make one party better off and no parties worse off.
Suppose Adam has a rare baseball card. He assigns no intrinsic value to baseball cards. Adam likes Beth, and somewhat values her happiness. Beth collects baseball cards, and would happily pay $100 for Adam's card.
If Adam just gives Beth his baseball card, is that a Pareto improvement? Naively, yes: he loses the card that he doesn't care about, and gains her happiness; she gains the card. Both are better off.
But I claim not, because if Adam has the card, he can sell it to Beth for $100. He would much prefer doing that over just giving her the card. But if Beth has the card, he can't do that. He assigns no intrinsic value to the card, but he can still value it as a trading chip.
Now suppose Adam has the baseball card but Beth also has a copy of that card. Then Beth has less desire for Adam's card, so this situation also isn't a Pareto improvement over the original. By giving something to Beth, we've made Adam's situation worse, even though Adam likes Beth and values her happiness.
And I think situations like this are common. The ability to give someone something they want, is a form of power; and power is instrumentally useful. And the less someone wants, the less able you are to give them something they want.
For a closer-to-reality example, the reddit comment that sparked this post said:
bringing Platform 3 back into use at Liverpool Street Underground Station was denied because the platform would not be accessible. Neither of the platforms currently in use for that line is accessible, so allowing Platform 3 to be used would be a Pareto improvement
The model here is that there are two parties, people who can access the platforms at Liverpool St and those who can't. If Platform 3 is brought back into use, the first group gains something and the second group loses nothing.
But I think that if Platform 3 is brought back into use, the second group loses some power. They lose the power to say "we'll let you bring back Platform 3 if you give us…". Maybe Platform 3 can be made accessible for $1 million. Then they can say "we'll let you bring it back if you make it accessible", but they can't do that if it's already back in use.
And they lose some power to say "if you ignore us, we'll make things difficult for you". Maybe it would take \$1 trillion to make Platform 3 accessible. If Platform 3 remains out of use, people are more likely to spend \$1 million to make their building projects accessible, because they've seen what happens if they don't. Conversely, if Platform 3 comes back, people are more likely to exaggerate future costs of accessibility. "If I say it costs \$1 million, I'll have to pay. If I say it costs \$10 million, maybe I won't."
I haven't researched the situation in question, and I expect that the actual power dynamics in play don't look quite like that. But I think the point stands.
(My original reply said: "If it's easier to turn an unused inaccessible platform into a used accessible platform, than to turn a used inaccessible platform into a used accessible platform - I don't know if that's the case, but it sounds plausible - then opening the platform isn't a Pareto improvement." That still seems true to me, but it's not what I'm talking about here. There are lots of reasons why something might not be a Pareto improvement.)
This doesn't mean Pareto improvements don't exist. But I think a lot of things that look like them are not.
Update 2018-02-02: some good comments on reddit and LessWrong. Following those, I have two things in particular to add.
First, that I like /u/AntiTwister's summary: "If you have the power to prevent another party from gaining utility, then you lose utility by giving up that power even if you are allies. There is opportunity cost in abstaining from using your power as a bargaining chip to increase your own utility."
Second, that there is a related (weaker) concept called Kaldor-Hicks efficiency. I think that a lot of the things that look-like-but-aren't Pareto improvements, are still Kaldor-Hicks improvements - meaning that the utility lost by the losing parties is still less than the utility gained by the winners. In theory, that means that the winners could compensate the losers by giving them some money, to reach a Pareto improvement over the original state. But various political and practical issues can (and often do) get in the way of that.
Posted on 27 January 2018
|
Comments
Epistemic status: Pure dilettantism. I have never used Go. This might make me unqualified to say what I'm about to say. But it's okay, because I use the word "seems" a lot.
In Go, if you have an unused import, your program fails to compile. This has made a lot of people mildly annoyed and been sometimes regarded as a bad idea, but not universally.
The devs decline to add a compiler flag to change this behaviour, "because compiler options should not affect the semantics of the language and because the Go compiler does not report warnings, only errors that prevent compilation". This strikes me as reasonable, if not the decision I personally would make.
Instead, they suggest this pattern:
import "unused"
// This declaration marks the import as used by referencing an
// item from the package.
var _ = unused.Item // TODO: Delete before committing!
- that is, add a line of code to trick the compiler into thinking that you're using the import, even though you're not. (Unless you forget to delete the trick line, which the compiler won't verify for you.)
This does not strike me as a very good substitute. With a compiler flag, I could turn it on while debugging and turn it off for production to make sure I had no unused imports. I could use a commit hook to keep unused imports out of the repository. By tricking the compiler, there's no particularly easy way to do this. (I suppose I could put the string "FAKEIMPORT" is a comment on those lines, and grep for that string. This is still not a great solution.)
I also refer to the devs' opinion that "if it's worth complaining about, it's worth fixing in the code. (And if it's not worth fixing, it's not worth mentioning.)" I claim that there's no fundamental difference between
and
import unused
var _ = unused.Item
Neither affects the semantics of the program, if we ignore that the first one doesn't compile. If one is worth complaining about, so is the other. But the devs are sending mixed signals. It seems the first is worth complaining about, because the compiler complains. But it seems the second is not, because the devs recommend it. This should be a sign that something about this whole situation is less than ideal.
(For myself, I would say that both are worth complaining about in production, and neither is worth complaining about when debugging. But the trick works equally well in both instances.)
There is another solution, in the form of a tool called goimports. The idea is that you don't write imports at all. If you have a symbol that isn't imported, it searches your filesystem for an appropriate package and adds an import line. If you have an unused import, it deletes it.
But word on the street is that some names are ambiguous, supplied by multiple packages, and goimports has no way to choose which one you mean. So if you comment out a line, and then uncomment it, goimports might add back a different import than the one you originally used. This, too, seems less than ideal.
All of which is to say: although I don't use Go, it seems to me that Go has a problem, and that the existing solutions aren't perfect.
I propose a new solution, which could be implemented as two new modes for goimports to run in or as one or two completely new tools.
In the first mode, this tool acts like goimports, but more conservatively. Instead of removing unused imports, it merely comments them out. And instead of searching your filesystem for packages, it merely searches your comment lines, and uncomments them if there's a match.
So if you're debugging, and comment out the only use of a package, this tool will comment out the import for you. When you uncomment that use, the import will be added back in, but without the ambiguous naming problem. At no point do you have to trick the compiler, so you don't have to remember to stop tricking the compiler.
In the second mode, this tool checks for commented out import lines, and tells you whether it found any (or optionally deletes them). It can be called in commit hooks, to prevent such lines from cluttering up a repository.
This seems to me like it would be an improvement on the status quo.
Posted on 13 January 2017
|
Comments
The monk Dawa had a clock that had stopped, and he was content. When he wished to know the hour, he would glance at the clock, and discover that it was noon.
One day a visiting friend commented on the clock. "Why does your clock say that the hour is noon, when I am quite sure that it is six in the evening?"
Dawa found this unlikely, for the hour had always been noon in his experience. But he had been instilled with the virtues of curiosity and empiricism. If the hour is noon, I desire to believe it is noon. If the hour is six in the evening, I desire to believe it is six in the evening. Let me not become attached to beliefs I may not want. Thus fortified, he sought out other clocks.
The time was indeed six in the evening. In accordance with the virtue of relinquishment, and gently laughing inside at his past foolishness, Dawa serenely set his broken clock forwards by six hours.
Posted on 22 December 2016
|
Comments
This is a story of me failing to do something, and some thoughts on how I might have succeeded.
A friend had a problem. He'd been recording some audio on his phone when the battery died, leaving him with a .m4a file that couldn't be played. He had a look at the contents and it contained a bunch of data, so he offered $40 if someone could recover the audio for him.
This seemed like a fun challenge that would exercise skills there isn't much call for. I didn't necessarily expect to succeed, but I decided to give it a go. (I only remember doing something like this once before, when I had a corrupt FAT partition that I managed to fix with some bit-flipping.)
To help, the friend provided two small files from the same app: one a successful recording, and one corrupt like the target file.
The simplest thing was to simply try playing the broken files with mplayer, just in case. It didn't work, and gave an error message saying (among other things) "moov atom not found".
The next thing was to look at all the files in a hex editor, which in this case was "hexdump -C piped into less" because I don't think I have a dedicated hex editor installed. I quickly noticed that the good recording had the bytes moov at location 0x1d, while the corrupt recordings both had the bytes free there.
I also noticed that all three files had the bytes mdat at location 0xc95, followed by some low-entropy data, and then some apparently high-entropy data that seemed to go on to the end of the file. I guessed that this was the actual audio data, while the start of the good recording was a valid audio header.
00000000 00 00 00 18 66 74 79 70 6d 70 34 32 00 00 00 00 |....ftypmp42....|
00000010 69 73 6f 6d 6d 70 34 32 00 00 0c 79 66 72 65 65 |isommp42...yfree|
00000020 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 00 |................|
*
00000c90 00 3f 3f 3f 3f 6d 64 61 74 01 40 22 80 a3 7f f8 |.????mdat.@"....|
00000ca0 85 2d 2d 2d 2d 2d 2d 2d 2d 2d 2d 2d 2d 2d 2d 2d |.---------------|
00000cb0 2d 2d 2d 2d 2d 2d 2d 2d 2d 2d 2d 2d 2d 2d 2d 2d |----------------|
*
00000da0 2d 2d 2d 2d 2d 2d 2d 2d 2d 2d 2d 2d 2e ff f1 0a |------------....|
00000db0 5a 5a 5a 5a 5a 5a 5a 5a 5a 5a 5a 5a 5a 5a 5a 5a |ZZZZZZZZZZZZZZZZ|
*
00000eb0 5a 5a 5a 5a 5a 5a 5a 5a 5a 5a 5a 5d e0 e2 14 b4 |ZZZZZZZZZZZ]....|
00000ec0 b4 b4 b4 b4 b4 b4 b4 b4 b4 b4 b4 b4 b4 b4 b4 b4 |................|
00000ed0 b4 b4 bc 00 e2 36 2e 70 5b 0c 09 88 8b b1 2a ae |.....6.p[.....*.|
00000ee0 9d 55 6c 14 4c 2a 2a 55 45 44 01 c5 35 93 14 a0 |.Ul.L**UED..5...|
The start of the target file. hexdump prints a * to indicate that several lines have been skipped which were identical to the one above. The audio data seems to start around position 0xed2.
So that gave me another simple thing to try. I took the first 0xc95 bytes from the good file, and byte 0xc95 onwards from the small corrupt file, and concatenated them.
head -c 3221 tinytest_notbroken.m4a > fixtest-1.m4a
tail -c +3222 tinytest_broken.m4a >> fixtest-1.m4a
After this, fixtest-1.m4a played in mplayer. It printed lots of warning messages while it did so, but whatever.
So I did the same thing with the target file, and recovered two seconds of the original audio. I could report to my friend that it started with him saying "um".
This is what I was expecting, since the good recording was only two seconds, and it would presumably have had the length in the header. But now I needed to work out how to lengthen it.
I played around with ffmpeg, but it didn't seem to have an option for "ignore the audio duration stated in the header", so it seemed I would have to fix the header myself.
ftyppm42 seemed like it might be a file type indicator, so I googled that. A few clicks led to the MP4 registration authority, which suggested that the relevant standard was called "ISO/IEC 14496-14". So I then googled "ISO/IEC 14496-14 track header", and found a pdf of the relevant standard. Unfortunately this is a high-context document, I didn't particularly understand it, and it didn't help me very much.
I also found wikipedia on MP4, which pointed me to ISO base media file format, ISO/IEC 14496-12. Google then gave me a pdf of that standard, which was much more detailed, helpful, and lengthy.
I didn't attempt to understand it all. But I searched for "mdat", and shortly after one of the hits, I found the following description of a data structure:
aligned(8) class MovieHeaderBox extends FullBox(‘mvhd’, version, 0) {
if (version==1) {
unsigned int(64) creation_time;
unsigned int(64) modification_time;
unsigned int(32) timescale;
unsigned int(64) duration;
} else { // version==0
unsigned int(32) creation_time;
unsigned int(32) modification_time;
unsigned int(32) timescale;
unsigned int(32) duration;
}
template int(32) rate = 0x00010000; // typically 1.0
template int(16) volume = 0x0100; // typically, full volume
const bit(16) reserved = 0;
const unsigned int(32)[2] reserved = 0;
template int(32)[9] matrix =
{ 0x00010000,0,0,0,0x00010000,0,0,0,0x40000000 };
// Unity matrix
bit(32)[6] pre_defined = 0;
unsigned int(32) next_track_ID;
}
Promising! My header contained the following two lines:
00000020 00 00 00 6c 6d 76 68 64 00 00 00 00 d4 6b 4f 0d |...lmvhd.....kO.|
00000030 d4 6b 4f 0d 00 00 03 e8 00 00 08 17 00 01 00 00 |.kO.............|
That's mvhd from the description, followed by four null bytes, followed by two identical 32-bit ints - the creation and modification times would naturally have been the same - and then two more ints.
timescale was 0x3e8, decimal 1000, which per spec means 1000 time units pass in a second. duration was 0x817, decimal 2071, indicating a track 2.071 seconds long. So presumably I need to edit this value.
What to set it to? As long as it's sufficiently long, it's not important. So I set it to 0x10000817, using emacs (in hexl-mode) as my editor, and tried again. No dice, it still cut off at two seconds.
So I searched "duration" in the same file, and found two more places to edit. One soon after the bytes tkhd, which used the same timescale as the mvhd; and one soon after the bytes mdhd, which had its own timescale. In this case the timescale was 0xac44, decimal 44100.
But adding 0x1000000 to both of these durations didn't help either.
(After one of these three edits - I don't remember which - mplayer started reporting the file as being 74 hours long. But it still cut out after two seconds.)
At this point I was up late and out of ideas. But I realized that I could just ask my friend to record another long track, and then use the header from that to do the job. So I left him instructions, plus some notes on where I'd got to, so someone else could pick up where I'd left off if that didn't work.
Then while I was asleep, someone else came along and fixed it for him before he tried that. I don't know how.
But here are some thoughts on how I might have proceeded, if my friend hadn't been able to record the longer audio.
For one thing, I might have been able to generate my own long file in ffmpeg. But attempting this now, I can't make it work. I concatenate several copies of the good recording, and get a file that starts with these three lines:
00000000 00 00 00 18 66 74 79 70 4d 34 41 20 00 00 02 00 |....ftypM4A ....|
00000010 69 73 6f 6d 69 73 6f 32 00 00 00 08 66 72 65 65 |isomiso2....free|
00000020 00 07 93 5e 6d 64 61 74 01 40 22 80 a3 7f f8 85 |...^mdat.@".....|
It plays fine. But when I try to mix it with the target file, it doesn't play. It complains about the missing moov atom, even though that's also missing in the working concatenated file. I'm not sure what's wrong.
Failing that, I could have recorded the long file myself in the same app my friend used, to spare his attention for things he actually wanted to be doing. (Which, after all, was the reason he was willing to pay someone else to fix the file.) I could also, for curiousity's sake, have recorded another short file, and attempted to find more durations by comparing the headers.
But perhaps the simplest thing would have been to take a completely different approach from the beginning. It turns out that other people have encountered this problem before, and paved the way for those like me. For example, someone on facebook posted this page, which teaches you to fix these files using a piece of software called "faad.exe". More research reveals that this is open source, and even available in portage.
(I also find references to FAAD if I google "fix corrupt m4a file".)
It looks like this was a case of "more haste, less speed". At least the haste was fun, but probably not worth the $40 I might have earned by being thorough.
Posted on 17 December 2016
|
Comments
I'd like to coin a term. The Sally-Anne fallacy is the mistake of assuming that somone believes something, simply because that thing is true.
The name comes from the Sally-Anne test, used in developmental psychology to detect theory of mind. Someone who lacks theory of mind will fail the Sally-Anne test, thinking that Sally knows where the marble is. The Sally-Anne fallacy is also a failure of theory of mind.
In internet arguments, this will often come up as part of a chain of reasoning, such as: you think X; X implies Y; therefore you think Y. Or: you support X; X leads to Y; therefore you support Y.
So for example, we have this complaint about the words "African dialect" used in Age of Ultron. The argument goes: a dialect is a variation on a language, therefore Marvel thinks "African" is a language.
You think "African" has dialects; "has dialects" implies "is a language"; therefore you think "African" is a language.
Or maybe Marvel just doesn't know what a "dialect" is.
This is also a mistake I was pointing at in Fascists and Rakes. You think it's okay to eat tic-tacs; tic-tacs are sentient; therefore you think it's okay to eat sentient things. Versus: you think I should be forbidden from eating tic-tacs; tic-tacs are nonsentient; therefore you think I should be forbidden from eating nonsentient things. No, in both cases the defendant is just wrong about whether tic-tacs are sentient.
Many political conflicts include arguments that look like this. You fight our cause; our cause is the cause of [good thing]; therefore you oppose [good thing]. Sometimes people disagree about what's good, but sometimes they just disagree about how to get there, and think that a cause is harmful to its stated goals. Thus, liberals and libertarians symmetrically accuse each other of not caring about the poor.
If you want to convince someone to change their mind, it's important to know what they're wrong about. The Sally-Anne fallacy causes us to mistarget our counterarguments, and to mistake potential allies for inevitable enemies.
Posted on 09 April 2016
|
Comments
I've created an interactive graph of historical levels of political polarization in the US House of Representatives. It would be tricky to embed in this blog, so I'm only linking it. Summary:
The x-axis on this graph is based on DW-NOMINATE left-right scores of each member of each U.S. House of Representatives from 1865 to 2015. This uses a member's voting record to measure the direction and extremity of their political views, regardless of party affiliation.
If a member's score on this axis is known, it's possible to predict their vote on any given issue with high confidence, given no other information about the member. Members whose votes are typically left-aligned receive negative scores, while members whose votes are typically right-aligned receive positive scores.
(However, see The Thin Blue Line That Stays Strangely Horizontal, which questions the validity of DW-NOMINATE.)
Background: I made this last year for a Udacity course, "Data Visualization and D3.js". I needed to submit a visualization for marking, and this was my submission. I'm grateful for feedback provided by Udacity and by some of my friends. Without that, the result would certainly have been worse.
The source is available on GitHub, including datasets and some python scripts I used to process them. The README also documents some of the design history.
I'm aware of one bug: in firefox (38.6.1 on linux), the legend appears to display the 5-95 and 25-75 percentile boxes identically. They're implemented as rects with fill-opacity: 0.3: the 25-75 boxes have two of these rects on top of each other. This is also how the paths on the graph itself are colored.
I assume there are other bugs.
Posted on 26 February 2016
|
Comments
I realized a few years ago that I was at least somewhat faceblind/prosopagnosic. A while back I took an online test out of curiousity, and scored low. They said that if I was in London and interested in further tests, I should leave my email address. A few days ago I went in for those tests, and now I have a PhD student (Katie) also telling me I'm faceblind. Which makes it official, I guess.
Next she wants to run EEGs on me, which should be cool. That will help work out where my brain is going wrong, in the long chain between "photons stimulate nerve endings in my eyeballs" and "I recognize a face" (whatever that means). Also, apparently there's a phenomon which sounds to me like blindsight, where some prosopagnosics' brains are clearly reacting to faces on some level that doesn't reach their consciousness. She wants to learn more about that too.
What follows is discussion of the tests, my scores, and what they mean. I've been given a powerpoint with my scores reported as percentiles, along with absolute scores and average control scores. 2% or lower is counted as "impaired". Percentiles are only given as integers, or as "<1%". On the day, Katie also gave me some numbers in terms of standard deviations (σ). Under a normal distribution, 2.5% would be approximately -2σ, but I'm not sure any of these results will be normally distributed, so I don't know if σ scores really tell me anything.
A note: if you think you might be faceblind, and you'd be interested in getting more detailed tests, it might be a good idea not to read the below. I expect it wouldn't significantly bias the results if you did, except for one bit that I've rot13ed. But I don't trust myself to make that call. If you're in London, you can take the above test like me and see what happens. Otherwise I'm not sure how you'd go about getting more tests.
The object/face recognition tests were "memorise these things, then we show you a sequence of things and you have to say if each of these things was a thing in the first set". The things were houses, cars, horses, and bald women's faces. I was bad at all of these: 4% for cars, 2% for houses, and <1% for horses and women. (Average score was higher for women than horses, and my score was higher for horses than women, so I'm worse at women than horses. I think Katie told me I was somewhere between -5σ and -6σ for women. Under normality, -5σ is one in thirty million, but this is clearly not normal.) So it seems I have some level of general object agnosia, but more specific prosopagnosia on top of that.
I was 11% for reading emotions from eyes, which is a point for Team Phil Does Not Have Aspergers (some of my friends are divided about that). In fact, the average score is 26 and I scored 23, and there were a few cases where I said an answer, then thought "wait no it's this" and didn't say anything because I wasn't sure if I should. (I was speaking my answer and Katie was recording it. I had to choose from four emotions, so I'm not sure why this wasn't recorded by a computer like most of the other tests.) So plausibly I'm actually above 11%.
I was <1% at famous face recognition, recognising five out of fifty that I'd been exposed to, out of sixty in total. (I got Jvyy Fzvgu, Uneevfba Sbeq, Dhrra Ryvmnorgu, Ebova Jvyyvnzf, and surprisingly Ovyy Pyvagba.) It seems that controls tend to get above 40, so even counting that "exposed to" is vague, I did really badly at this. I think Katie said I was -9σ, which would be one in 10^19 under normality.
I'm <1% at the Cambridge Memory Test for Faces, which is the one I linked above. I actually scored worse in the lab than online. (47% versus 58%, IIRC, with a control average of 80%, and 60% indicating impairment. But the lab score I've been given is 34 against control of 58, so it's clearly been adjusted.) There could be any number of reasons for this, including "chance". But when I took it online, I often thought that one of the faces looked a little like Matt Damon, and chose that one. I like to think that "mistaking people for Matt Damon" is the way forward in face recognition.
I was somewhat okay at half of the Cambridge Face Perception Test. In this one, they showed me a face at an angle, and below it the same face face-on, six times, with varying degrees of modification. I had to order them according to how similar each was to the original face, within a minute. For half the tests, the faces were all upside down. For all of the tests, they all looked incredibly similar and my instinctive reaction was WTF.
On the upright test, I got <1%. On the inverted test, I got 7%. One strategy I used a few times was to focus on the lips, specifically on the size of the dip in the bow. I just ordered them according to that. I guess it helps, but I found it a lot easier for inverted faces.
Doing better at inverted would seem to suggest that I'm doing some kind of holistic face processing that goes wrong and blocks off later avenues for perception. Buuut, objectively I scored worse on the inverted faces, just not as much worse as average, so I'm not sure if this does suggest that. (And I'm not sure it is "objectively" - if all the faces had been assigned to the other condition, would my scores have changed?)
Hypothetically, high scores on both tests could indicate my problem is with memory, not initial perception. The low score here doesn't mean I don't have a problem with memory, but it does seem to hint that I do have a problem with initial perception. And I suspect the famous faces test points at me also having a memory problem.
Posted on 19 January 2016
|
Comments
Inspired by Slate Star Codex
Explaining a joke is like dissecting a frog: it's one way to learn about frogs. If you want me to explain any of these, ask, and I will explain without making fun of you.
"I hear someone playing a triangle in the corridor," said Tom haltingly.
"We've got to overturn every last insect in this garden," said Tom flippantly.
"Goose feathers are annoyingly fragile," said Tom, breaking down.
"Anastasia gives me pins and needles," said Christian gratingly.
"I miss my submissive," René opined.
"I didn't do it, and nor did any of my siblings," Tom insisted.
"It's not much paint, it won't hurt to run your tongue up it," said Tom metallically.
"I'm so sick, even my flu has the flu," said Tom metallurgically.
"It's pitch black and I can hear a monster doing arithmetic," said Tom gruesomely.
"Man City don't hold a candle to the real heros of Manchester," said Tom manually.
"I just bought Manchester United," said Tom virtuously.
"Lancelot told me I was his favourite!" said Tom, surprised.
"I don't think this tube of semen is entirely straight," said the incumbent.
"I can fit inside my GameCube!" said Tom inconsolably.
"In a former life, I was a priest in pre-Columbian Peru," said Tom inconsolably.
"I need a name for my squid-and-flatfish restaurant," said Tom inconsolably.
"I make a living as the red tellytubby," said Tom, apropos.
"I'm doing crunches so I can get a six-pack," said Treebeard absently.
"I'm half-fish and made of lithium," said Treebeard limerently.
"Figure three plots counts of close-ups on male versus female genitals," said Tom pornographically.
"My breasts don't have enough room in this corset," said Victoria, double depressed.
"Bring me the head of my enemy," said Emacs vicariously.
"I have affirming the consequent, base rate neglect, and now also ad hominem," said Tom, getting cocky.
"We lost the treaty, so we had to ratify it again," said Tom, resigned.
"I'm in the group supporting Shiva's wife," said Tom with satisfaction.
Posted on 01 January 2016
|
Comments
Sometimes you (or at least, I) want to run a command for its output, but also want to pipe it through another command. For example, see the results of a find but also count how many hits it got. I've sometimes lamented that there's no easy way to do this. But the other day I had a flash of insight and figured out how:
find . | tee /dev/stderr | wc -l
proc1 | tee /dev/stderr | proc2 # general case
(I'm pretty proud of this. I don't know if it's original to me, but I discovered it independently even if not.)
tee will print the output of proc1 to both stdout and stderr. stderr goes to the terminal and stdout goes to proc2.
You can make it more convenient with an alias:
alias terr='tee /dev/stderr | '
find . | terr wc -l
(Putting a pipe in an alias seems to work in both zsh and bash.)
If you want to concatenate the streams, to pipe them to another process, you can use subshells:
proc1 | ( terr proc2 ) 2>&1 | proc3
but note that stderr output from proc2 will also get sent to proc3, unless you send it somewhere else. I haven't yet thought of a use for this.
There are potential issues with buffering here. I'm not aware that tee makes any promises about which order it writes the streams in. It's going to be interlacing them while it writes, so that it doesn't need to keep a whole copy in memory. So (if the input is large enough) proc2 will be receiving input before it's finished being written to stderr, and might start writing output, and then the output streams can get interlaced.
For some values of proc2, commands which start printing before they've finished reading, this is inevitable. But I think useful proc2s are likely to be aggregators - by which I mean, commands which can't do anything until they've finished reading all their input. In my tests so far, those have been safe, but that doesn't prove much.
We can do a more reliable check with strace:
find . | strace tee /dev/stderr | wc -l
By the looks of things, tee will read into a buffer, then write it to stdout (the pipe), then write it to the specified target (stderr, which goes to the terminal), and repeat to exhaustion. But the important thing is, it doesn't close any file descriptors until it's finished writing everything, and then it closes the target before it closes stdout. If this is consistent amongst tee implementations - and it seems sensible - then aggregators almost definitely won't interlace their output with the output from proc1. I don't want to say "definitely", because there might be other stuff going on that I haven't accounted for. But at any rate, tee will finish writing before the aggregator starts.
Anyway, I see this as being the sort of thing that you're likely use manually, not in an automated process. So if the output does get interlaced a little, it's probably not that big a deal.
Posted on 07 October 2015
|
Comments
Preface: I wrote this report for Udacity's "Explore and Summarize Data" module. The structure is kind of strange for a blog post, but I'm submitting the finished report essentially unchanged.
One thing I will note. I find that the cycle hire usage doesn't change much throughout the year. Shortly after submitting, I read this article which finds that it does vary quite a lot. I'm inclined to trust that result more. It's intuitively sensible, and it looks directly at the number of rides taken, instead of looking at a proxy like I do.
Take this as evidence for how much to trust my other results.
My goal is to investigate usage of the London cycle hire scheme, and in particular how it varies with the weather. I'm running an analysis from July 2013 to June 2014.
I'm using two data sets here. Daily weather data comes from Weather Underground, using the weather station at London Heathrow airport.
(London City Airport is closer to the bike stations that I use, but the data
from that airport reports 0 precipitation on every single day. The data from
Heathrow seems to be more complete, and I expect it to be almost as relevant.)
I collected the cycle hire data myself, over the course of the year, by downloading CSV files from an unofficial API which now appears to be defunct. It has a granularity of about ten minutes. That's about 50,000 entries per docking station for the year, so for this analysis, I'm only using the data from four docking stations near my office.
All data and source code used for this project can be found in the git repository.
Exploring the weather data
Temperature


These variables measure the minimum, average, and maximum daily temperatures.
The graphs all look similar, and overlap a lot. The shape is a little
surprising, as I didn't expect the density graphs to be bimodal. It could
potentially be caused by significant differences between summer and winter, with
an abrupt shift between the two.
Rainfall


According to the rain column, There are over 225 rainy days and only about 125 non-rainy days. But by far the most common bin for precip.mm is the leftmost one. Table of values of precip.mm:
##
## 0 0.25 0.51 0.76 1.02 2.03 3.05 4.06 5.08 6.1 7.11 7.87
## 207 35 20 9 17 22 12 8 12 4 4 2
## 8.89 9.91 10.92 11.94 13.97
## 3 5 2 1 2
Although more than half of observations have rain == TRUE, more than half of them also have precip.mm == 0, which needs more investigation. Rainfall as measured by precip.mm versus as measured by rain:


The two measures don't always agree. Sometimes rain is false but precip.mm is nonzero; and often rain is true but precip.mm is zero. Neither of those is surprising individually: if rain is only counted when the rainfall exceeds a certain threshold, then that threshold could be large (giving false/nonzero) or small (giving true/zero). But the combination suggests that that isn't what's going on, and I don't know what is.
This table counts the anomalies by turning precip.mm into a boolean zero/nonzero (false/true) and comparing it to rain:
##
## FALSE TRUE
## FALSE 119 9
## TRUE 88 149
There are 88 instances of true/zero, 9 instances of false/nonzero, but the cases where they agree are the most common.
I find precip.mm to me more plausible here. I feel like fewer than half of days are rainy. This website agrees with me, saying that on average, 164 days out of the year are rainy (rain - 237, precip.mm - 158).
Wind


These three measures of wind speed are all averages. wind is simply the average wind speed over a day. wind.max is the daily maximum of the average wind speed over a short time period (I think one minute). gust is the same thing, but with a shorter time period (I think 14 seconds).
Unlike with temperature, the three measures look different. All are right-skewed, although gust looks less so. There are several outliers (the isolated points on the box plots), and the quartiles don't overlap. The minimum gust speed (about 24) is almost as high as the median wind.max.
Exploring the bike data
Time between updates

There are a few outliers here. Not all the lines are visible due to rendering artifacts, but above 5000, we only have five entries:
## name prev.updated updated
## 46779 Earnshaw Street 2013-10-03 08:50:23 2013-10-13 09:20:28
## 46899 Southampton Place 2013-10-03 08:50:22 2013-10-13 09:20:27
## 46918 High Holborn 2013-10-03 08:50:24 2013-10-13 09:20:30
## 47049 Bury Place 2013-10-03 08:50:26 2013-10-13 09:20:32
## 175705 Southampton Place 2014-06-20 17:36:06 2014-06-30 08:30:03
The first four of these happened when my collection script broke and I failed to realize it. The other occurred when Southampton Place was taken out of service temporarily.
Let's zoom in on the lower ones:

There are several instances where the time between updates is unusually large, on the order of hours or days. The times of entries with between 2000 and 5000 minutes between updates:
## name prev.updated updated
## 32650 High Holborn 2013-08-31 15:10:07 2013-09-02 12:30:05
## 32660 Bury Place 2013-08-31 15:10:08 2013-09-02 12:30:07
## 32672 Southampton Place 2013-08-31 15:10:05 2013-09-02 12:30:04
## 32674 Earnshaw Street 2013-08-31 15:10:06 2013-09-02 12:30:05
## 38546 High Holborn 2013-09-14 22:39:00 2013-09-16 08:24:22
## 38719 Bury Place 2013-09-14 22:39:02 2013-09-16 08:24:23
## 38734 Southampton Place 2013-09-14 22:38:58 2013-09-16 08:24:20
## 38735 Earnshaw Street 2013-09-14 22:38:59 2013-09-16 08:24:21
## 84066 Bury Place 2013-12-27 15:40:08 2013-12-29 23:10:14
## 84069 High Holborn 2013-12-27 15:40:06 2013-12-29 23:10:13
## 84073 Southampton Place 2013-12-27 15:40:05 2013-12-29 23:10:11
## 84078 Earnshaw Street 2013-12-27 15:40:05 2013-12-29 23:10:12
## 84186 Earnshaw Street 2013-12-30 00:10:05 2013-12-31 13:10:07
## 84202 High Holborn 2013-12-30 00:10:06 2013-12-31 13:10:09
## 84269 Southampton Place 2013-12-30 00:10:05 2013-12-31 13:10:06
## 84330 Bury Place 2013-12-30 00:10:07 2013-12-31 13:10:11
## 89443 Southampton Place 2014-01-12 20:20:10 2014-01-14 18:40:07
## 89459 High Holborn 2014-01-12 20:20:13 2014-01-14 18:40:11
## 89467 Bury Place 2014-01-12 20:20:14 2014-01-14 18:40:16
## 89524 Earnshaw Street 2014-01-12 20:20:11 2014-01-14 18:40:09
## 121381 Earnshaw Street 2014-03-15 14:50:06 2014-03-17 01:50:04
## 121398 High Holborn 2014-03-15 14:50:07 2014-03-17 01:50:05
## 121444 Bury Place 2014-03-15 14:50:10 2014-03-17 01:50:07
## 121591 Southampton Place 2014-03-15 14:50:05 2014-03-17 01:50:04
## 133765 High Holborn 2014-04-11 16:59:37 2014-04-14 01:29:07
## 133900 Earnshaw Street 2014-04-11 16:59:36 2014-04-14 01:29:05
## 133961 Bury Place 2014-04-11 16:59:38 2014-04-14 01:29:08
## 134027 Southampton Place 2014-04-11 16:59:35 2014-04-14 01:29:05
It looks like these happened to all stations simultaneously, suggesting problems with either my collection script or the API, rather than problems with individual locations.
Entries with less than 60 minutes between updates, no longer on a log scale:

In the vast majority of cases, updates are approximately ten minutes apart. This encourages me to take a subset of the data (bikes.all -> bikes), considering only entries with d.updated less than 15 minutes. This eliminates many outliers in future graphs.
Date and time of update


All times of day are approximately equally represented to within ten minutes, which is good. There are five noticeable troughs preceeded by spikes, but they probably don't signify much. Dates are a lot less uniform, however. Even apart from the ten-day period where my script was broken, many days have significantly fewer updates than typical, and some have none at all.
Number of days spent with a given number of active docks

It was common for every station to report less than a full complement of docks. At least two had a full complement for less than half the time (High Holborn and Bury place are unclear in that respect). This isn't surprising, since a bike reported as defective will be locked in, using up a slot but not being available for hire.
Journeys taken throughout the year

The time of year makes very little difference to the number of rides. There appears to be a slight sinusoidal relationship, but it's very weak. (I didn't do a PMCC test because that assumes that any relationship is linear, which we would naively expect not to be the case here, and also doesn't look true from the graph.)
Journeys by weekday



Fewer journeys are taken on weekends. The median number of bikes available doesn't change much throughout the week (5 on monday and friday, 4 on other days), but the distribution does. Saturday and Sunday have noticeably different shapes to the others. They have a single peak, while weekdays are somewhat bimodal, with a small peak where the station is full (probably when people are arriving at work).
(Since the stations have different numbers of docks, I did a graph of fullness rather than of number of bikes. The density plot doesn't show peaks exactly at 0 and 1 because of how the density window works, but histograms of num.bikes and num.spaces show that that's where they are. It would be difficult to use a histogram for this graph because there's no sensible binwidth.)
Change in number of bikes between updates

##
## Pearson's product-moment correlation
##
## data: bikes$num.bikes and bikes$prev.num.bikes
## t = 2466.8, df = 173250, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.9859301 0.9861908
## sample estimates:
## cor
## 0.986061
There's very strong correlation between the number of bikes in adjacent entries. This is as expected, especially given what we saw about d.num.bikes previously. The colors here don't show any particular station-dependent trends.
Number of bikes at any given time

The correlation also looks strong between the number of bikes at each station at any given time. Since they're all close to each other, that's not surprising. The time is a big factor, with large numbers of bikes in the stations during office hours, and few numbers in the evening and early morning. There's a slight dip around 1pm, which could be related to people using them on their lunch breaks.
This graph gives an overview of global trends, but I mostly use the bikes at specific times. We can zoom in on those:
Number of slots available at 0930
(when I'm trying to arrive at work)
This is a proportional frequency plot: within each facet of the graph, the heights of the bins add up to 1. Only weekdays are considered.

About 40% of the time, Earnshaw street has no spaces. That's actually less than I'd realized. It's directly outside my office, and I haven't even been checking it because I'd assumed it was always full.
And at 0940
(in case I'm running late)

If I'm late, I have slightly less chance of finding a docking station, but not much less.
Combining the two
Journeys taken on rainy vs. non-rainy days
Here, rain is the original variable in the dataset, and rain2 simply measures whether precip.mm is nonzero. We have graphs looking at d.num.bikes on each type of day, and tables comparing its mean absolute value.

## Source: local data frame [2 x 2]
##
## rain mean(abs(d.num.bikes))
## 1 FALSE 0.5160167
## 2 TRUE 0.4156172

## Source: local data frame [2 x 2]
##
## rain2 mean(abs(d.num.bikes))
## 1 FALSE 0.4824637
## 2 TRUE 0.4073405
## Source: local data frame [4 x 3]
## Groups: rain
##
## rain rain2 mean(abs(d.num.bikes))
## 1 FALSE FALSE 0.5184101
## 2 FALSE TRUE 0.4755501
## 3 TRUE FALSE 0.4351990
## 4 TRUE TRUE 0.4042656
Earlier I said I feel like precip.mm is more accurate than rain. Despite that, rain seems to be capturing something that precip.mm doesn't, because bike usage responds slightly more to it. This would seem to suggest that days where rain is true but precip.mm is zero have less bike usage than average; and indeed this is what we see.
Taking rain to be our measure, slightly over 70% of observations had no bikes added or removed on rainy days, and slightly under 70% on non-rainy days. The mean absolute difference is about 25% higher on non-rainy days.
Foggy versus non-foggy days

## Source: local data frame [2 x 2]
##
## fog mean(abs(d.num.bikes))
## 1 FALSE 0.4488018
## 2 TRUE 0.4568736
Journeys by temperature and wind:

##
## Pearson's product-moment correlation
##
## data: bikes$t and abs(bikes$d.num.bikes)
## t = 31.414, df = 173250, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.07057403 0.07993830
## sample estimates:
## cor
## 0.07525782

##
## Pearson's product-moment correlation
##
## data: bikes$wind and abs(bikes$d.num.bikes)
## t = -22.389, df = 173250, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## -0.05840721 -0.04901677
## sample estimates:
## cor
## -0.05371317
Unlike rain, it seems that fog, wind and temperature make approximately no difference. The mean absolute difference in number of bikes is about the same regardless of fog, and the correlation between that and temperature/wind is close to zero.
Number of bikes at any given time, depending on rain:

Rain reduces the variance, with fewer bikes during office hours and more outside of them.
Reformatting
With the data in the current format, not all the questions we want to ask are easy. For example: how does the number of bikes at one station correlate with another at any given time? I previously said it “looks strong”, but that's pretty vague.
To answer questions like that, we need to be somewhat forgiving with our definition of 'any given time'. Updates don't necessarily happen simultaneously, so we need to bin them together.
I'm going to create bins ten minutes wide, and assign every observation to a bin. Then in each bin, we can ask how many bikes were at each station. Using this, we can check correlation between each station:

Correlations range between 0.703 and 0.758, and the scatter plots and density histograms all look pretty similar. Does the correlation depend on time? Let's go for 0930, 1800, midnight, and noon.




The correlations are almost all lower. That surprised me, but I think it's an example of Simpson's paradox. I note that the darkest points in the graph are at midnight, with no bikes in any station much of the time. Bikes are periodically moved in vans to account for anticipated demand; I assume that these stations are emptied most nights to prepare for people coming to work in the morning.
An interesting point is that the weakest correlation on any of the graphs is 0.149, between Earnshaw Street and Bury Place at 1800. But the strongest correlation at a specific time is 0.757, also between those two stations, at 0930.
We also see the density charts sometimes having very different shapes, especially at 0930 and 1800. But this seems to be at least partly to do with the way that ggpairs chooses the axes on its density plots. For example, here's 0930:

The troughs look a lot less significant now.
We can view a histogram of the total number of bikes available at different times:

We see heavy leftward skews overnight, with much flatter (but somewhat right-skewed) distributions during office hours, and gradual transitions between the two.
We can also check correlation between times more distant than a single tick. If I check the slots available when I leave the house, can I learn how many will be there when I arrive?

##
## Pearson's product-moment correlation
##
## data: at.0900 and at.0930
## t = 68.675, df = 1228, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.8785868 0.9017383
## sample estimates:
## cor
## 0.8907389
This is good correlation! Does it depend on the rain?

##
## Pearson's product-moment correlation
##
## data: at.0900[rain] and at.0930[rain]
## t = 55.466, df = 816, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.8737218 0.9025687
## sample estimates:
## cor
## 0.8890242
##
## Pearson's product-moment correlation
##
## data: at.0900[!rain] and at.0930[!rain]
## t = 39.748, df = 410, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.8692649 0.9093735
## sample estimates:
## cor
## 0.8910456
Not much, if at all.
We can construct a model
##
## Call:
## lm(formula = at.0930 ~ at.0900, data = spaces.0900.0930)
##
## Residuals:
## Min 1Q Median 3Q Max
## -9.334 -1.502 0.561 1.708 16.477
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -1.43496 0.15556 -9.225 <2e-16 ***
## at.0900 0.97899 0.01426 68.675 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.802 on 1228 degrees of freedom
## (69 observations deleted due to missingness)
## Multiple R-squared: 0.7934, Adjusted R-squared: 0.7932
## F-statistic: 4716 on 1 and 1228 DF, p-value: < 2.2e-16
with an R2 of 0.79, which is okay. But this isn't the best we can do, because it groups all stations together. Ideally we would create one model per station, with inputs from every station.
##
## Call:
## lm(formula = at.0930 ~ sp + hh + bp + es, data = spaces.tmp[spaces.tmp$name ==
## "Southampton Place", ])
##
## Residuals:
## Min 1Q Median 3Q Max
## -8.566 -1.857 -0.148 1.152 15.420
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.79625 0.47090 -1.691 0.0919 .
## sp 0.74101 0.04179 17.731 <2e-16 ***
## hh 0.05424 0.05307 1.022 0.3075
## bp 0.11811 0.05092 2.320 0.0210 *
## es 0.07909 0.04550 1.738 0.0832 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.17 on 296 degrees of freedom
## (17 observations deleted due to missingness)
## Multiple R-squared: 0.736, Adjusted R-squared: 0.7324
## F-statistic: 206.3 on 4 and 296 DF, p-value: < 2.2e-16
##
## Call:
## lm(formula = at.0930 ~ sp + hh + bp + es, data = spaces.tmp[spaces.tmp$name ==
## "High Holborn", ])
##
## Residuals:
## Min 1Q Median 3Q Max
## -7.4068 -1.1295 0.1503 1.2304 8.3941
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -2.87268 0.29894 -9.610 < 2e-16 ***
## sp 0.08354 0.02653 3.149 0.00181 **
## hh 0.76021 0.03369 22.567 < 2e-16 ***
## bp 0.09533 0.03232 2.949 0.00344 **
## es 0.15937 0.02888 5.518 7.5e-08 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.012 on 296 degrees of freedom
## (17 observations deleted due to missingness)
## Multiple R-squared: 0.8349, Adjusted R-squared: 0.8327
## F-statistic: 374.2 on 4 and 296 DF, p-value: < 2.2e-16
##
## Call:
## lm(formula = at.0930 ~ sp + hh + bp + es, data = spaces.tmp[spaces.tmp$name ==
## "Bury Place", ])
##
## Residuals:
## Min 1Q Median 3Q Max
## -7.3465 -1.3008 0.3121 1.4809 9.4211
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -4.28068 0.32734 -13.077 < 2e-16 ***
## sp 0.18778 0.02907 6.460 4.32e-10 ***
## hh 0.03132 0.03687 0.850 0.396253
## bp 0.91255 0.03538 25.796 < 2e-16 ***
## es 0.11197 0.03160 3.543 0.000459 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.201 on 295 degrees of freedom
## (18 observations deleted due to missingness)
## Multiple R-squared: 0.8969, Adjusted R-squared: 0.8955
## F-statistic: 641.5 on 4 and 295 DF, p-value: < 2.2e-16
##
## Call:
## lm(formula = at.0930 ~ sp + hh + bp + es, data = spaces.tmp[spaces.tmp$name ==
## "Earnshaw Street", ])
##
## Residuals:
## Min 1Q Median 3Q Max
## -7.8978 -1.4508 0.3118 1.3272 11.8323
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -2.98653 0.35005 -8.532 7.60e-16 ***
## sp 0.05579 0.03107 1.796 0.0735 .
## hh 0.03405 0.03945 0.863 0.3887
## bp 0.17361 0.03785 4.587 6.65e-06 ***
## es 0.83329 0.03382 24.638 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.356 on 296 degrees of freedom
## (17 observations deleted due to missingness)
## Multiple R-squared: 0.8579, Adjusted R-squared: 0.856
## F-statistic: 446.9 on 4 and 296 DF, p-value: < 2.2e-16
Southampton Place has slightly regressed, but the others have improved slightly. In particular, Bury Place gets an R2 of 0.89, which is pretty good. (It's important to note that this doesn't make our model worse for Southampton Place than the aggregate model. The aggregate model was just overconfident on that station.)
Final plots and summary
Plot 1

The total number of bikes available changes gradually throughout the day, with few bikes typically available at night, but often many available during the daytime. The distribution looks left-skewed from around 10:00 to 17:00, and right-skewed from around 19:00 to 07:30. The left skew is never as extreme as the right skew, but because the stations have different numbers of slots, that doesn't tell us much.
Plot 2

This time around, I restricted the graph to weekdays only. It's rare for the number of stations to go up between 09:00 and 09:30. All four stations have similar usage patterns.
At 09:00, if there are five or fewer spaces available, it looks as though the most common single outcome at 09:30 is no spaces at all.
Points above the dotted black line are ones where more spaces were available at 09:30 than at 09:00. (Caveat: I've applied slight jittering, so points very close to that line are ones where the same number of spaces were available.) There are obviously much fewer of them. However, the top-left corner of the graph has a few points in it where the bottom-right corner is empty. The number of bikes never goes down by more than eleven, but it goes up by as much as fifteen.
Plot 3

I took advantage of binning to calculate specific summary functions. All stations show similar patterns: at night, there are few bikes available; during office hours, there are almost always some, and the 10-90 percentile range is a lot higher. The trough around 1pm in the previous version of this plot no longer shows up, which makes me suspect it was simply an artifact of the smoothing method.
During the day, the number of bikes available is generally ranked by the number of docking slots at each station - so High Holborn has the least, and Bury Place has the most. When the bikes are taken around 18:00, High Holborn seems to lose them more slowly than the other stations. For Earnshaw Street and especially Bury Place, the 90th percentile lines suggest that those two stations were often completely full.
Reflection
I've learned a lot about how to fight ggplot when it doesn't do exactly what I want by default, and in particular about how to shape my data for it.
I feel like a data frame isn't an ideal structure for the data I have. The fact that I had to create prev.* and d.* copies of those columns that need it seems suboptimal, ideally I would have wanted to be able to refer directly to offset rows in the data. (For example, there's currently no easy way to ask “what's the difference between the number of bikes now and 30 minutes ago?”) But I couldn't find anything that worked better. In particular, time series only allow one data type, so I would have had to fight to use them at all, and I don't know if they would have been any more useful.
My data set itself isn't ideal, particularly in the amount of missing data. Unfortunately, I don't think any better historical bike record data is available. I think I have enough data to trust my conclusions.
In general, it seems that weather doesn't have much impact on bike usage. I checked rain, fog, temperature and wind speed, and only rain made a significant difference. But since the rainfall data seems to be internally inconsistent, I don't know how much we can learn from it. It would be useful to validate it from another source. We might also learn more with finer-grained weather data. For example, when predicting bike availability at a specific time, it doesn't help much if we know whether or not it rained at all on a given day; but it might help more to know whether it was raining at that particular time.
On the other hand, we can make pretty good predictions about future bike (and slot) availability just from current availability. An ambitious future project might be a prediction system. A user could specify a station and an arrival time, and the system could tell her how likely it would be that she could find a slot in that station and nearby ones, and suggest an earlier arrival time that would increase that chance.
One thing I didn't examine was public holidays. For example, we might ask whether, on plot 2 above, many of the points where spaces were freed up fell on holidays. (We can calculate 85 points above the line, and only 8*4 = 32 of them could be on public holidays, but that's still potentially a third of them.)
After initially submitting this report, I noticed a big problem. All timestamps were collected and reported in physical time, but bike usage patterns are going to be related to clock time. So some of my graphs, particularly later ones, were mixing in data from two different clock times (e.g. 09:00 and 10:00) as if they were the same. My first submission was rejected for unrelated reasons, and I've corrected the error in all future versions.
Posted on 19 August 2015
|
Comments
(Content note: minor untagged spoilers for the solutions to certain logic puzzles. No major spoilers.)
(Epistemy note: It’s impossible to talk about how easy/hard a puzzle is that I discovered the answer to years ago, sometimes without working it out for myself. I’m about to do that anyway.)
There seems to be some kind of taxonomy for logic puzzles and how hard they are and the sort of strategies that are needed to solve them.
This might be too subjective to be worth talking about, but I suspect not, and the way to find out is to talk about it and see if people understand me, so without further ado:
Let's vaguely pretend that logic puzzles have a sort of fundamental particle which is the insight. You collect insights, and then you use insights to collect other insights, and eventually you win.
Now I'm going to describe five types of puzzle.
Deep: For example, the blue eyes puzzle. I consider this one to be actually pretty easy. You ask what happens with one blue-eyed person, then two, then three, and just proceed by induction. (Even if you don’t know the terms common knowledge and mutual knowledge and the difference between them, in the two-person case you can say “she tells Alice that Bob can see blue eyes” and in the three-person case you can say “she tells Alice that Bob knows that Carol can see blue eyes” and so on.) There's only one real insight, which you apply lots of times. Or just a couple of times until you get bored and assume/prove the pattern continues.
(I feel like there's a lot of similarity between solving a logic puzzle and proving a math theorem. Here, the math equivalent is proof by induction.)
Wide: Cheryl’s birthday is also quite easy, but what difficulty it has lies in breadth rather than depth. Every line tells you something new, and you need to extract a different insight from each of them.
(Math equivalent: a theorem with a complicated statement but a proof where every line just reads "because X, Y".)
Trivial puzzles are the limiting case of either of the above. I don't know any famous ones, but the blue-eyed puzzle with one blue-eyed person would count.
(Math equivalent: modus ponens.)
Verify: Then there are problems where as far as I know you kind of just have to intuit (or guess) the solution, and then demonstrate that it works. (The demonstration is a recursive problem that deserves its own classification, or possibly doesn't even count as a logic puzzle. Often it is just math.) The key insight is hidden away, with no hints as to what it might be. The fork in the road is a good example of this, I think, where the demonstration has reasonable claim to being trivial.
It’s a very fuzzy and personal category, because there are patterns that you may be able to recognize which would move it towards wide.
(Math equivalent: a proof which introduces some new device that you don't know where it came from, but it turns out to be exactly what you need.)
Learn: And there are probably also problems where, if you happen to know the right thing and it comes to mind at the right time, this will be trivial (or wide or…). Otherwise you’ll have to deduce thing for yourself, good luck with that. I can’t offhand think of any canonical examples.
This category may be even fuzzier and more personal, and probably overlaps a lot with verify, and is hard to detect except in hindsight. (If you can work out what you need to know, it moves towards wide or verify.)
Of course every puzzle has a thing which is the solution to that particular puzzle; and many puzzles rely on the ability to do basic arithmetic or other such skills. Those obviously "shouldn't count" to clasify a puzzle as learn, but I don't have a principled way to distinguish them from things that should.
(Math equivalent: a proof in complex analysis that relies on an obscure theorem from number theory.)
I don't intend for these descriptions to be fully general. I think that they're pointing at real clusters in puzzlespace, but don't fully capture the essences of those clusters.
Even if they did, I expect these clusters are going to fail to capture a lot of variation, and attempting to shove things into them will sometimes be a silly thing to do. But let's make a start with them, and try to classify some problems that come to mind:
This transfinite epistemic logic puzzle challenge is mostly a combination of deep and wide I think, but also some learn because I wouldn't recommend attempting it if you don't know about order types. I didn't find it overly challenging. (Except that reading the solution, I no longer remember if I got the answer exactly correct. I might have made a fencepost error.)
I haven't solved the sum and product puzzle, but as far as I've got has been a wide. I'm pretty sure I could finish it with brute force, but I suspect there's an elegant way to do it which is either a verify or a learn, possibly involving number theory.
The hardest logic puzzle ever is the fork in the road on steroids. Given the solution, proving that that solution works would be a moderately challenging wide puzzle. Generating it from scratch seems to require multiple levels of verify and wide.
The hundred prisoners problem is very verify. The verification step is a combinatorics problem. (I feel like there are a lot of problems based on having a hundred prisoners and an intellectually peverse gatekeeper, and I feel like most of them are verify. Here's another example.)
This card trick/puzzle is a verify. (I'm pretty sure I have a solution, but I've only verified it in my head, and I didn't fully work out the details. My solution is very different to the posted one. Arguably, the posted solution has a learn on the pigeonhole principle and mine doesn't.)
The pirate game is a little deep and not much else.
Logic grid puzzles are wide. They differ from Cheryl's birthday in that every clue needs to get used multiple times, but each clue-application is still straightforward. That doesn't mean they're easy.
Here are some other features that we might want to talk about.
Logic puzzles often (not always) have a number of characters. Sometimes you know more than/just as much as the characters, and need to work out how each of them will act. Sometimes you know less, and need to work out what they know from how they act.
Sometimes you need to come up with a strategy rather than a specific answer. Sometimes there are multiple strategies. Sometimes there's a foolproof strategy, other times you just need to find one as effective as possible. If that's the case, then it might be difficult to work out exactly how effective it is, even if it seems obviously more effective than the naive strategy; and proving that it's optimal might be harder again. It took three years to prove optimality on the hundred prisoners.
Different puzzles require different "levels" of theory of mind, and I suspect there's a lot of variation in how well people can keep track of those without accidentally collapsing them. "Alfred knows that Bernard doesn't know" might become just "Bernard doesn't know"; and "Alice doesn't know that Bob knows that Carol can see blue eyes" might become just "I have no idea what's going on".
Another future direction to explore might be a taxonomy of video game puzzles. I think there'd be some similar themes, but for example, video games can have progression in a sense that doesn't exist in most of the puzzles I've described so far.
Two senses, in fact. You can progress within a level, when you change the board state. Different games/levels have different attitudes to (a) how many ways you can do this at any given moment, and (b) whether it's possible to make a level unsolvable.
But also a level can teach you something by holding your hand, and in future levels you can use that without having your hand held. So level ten would have seemed impossible if you'd started with it, but after levels one through nine it's just challenging enough to be fun. Logic puzzles can have this: the fork in the road teaches you a tool to apply to THLPE. But the level order in video games gets to be designed deliberately. Whereas in real life, I mostly encounter logic puzzles by accident, with no guarantee that I've already encountered any precursors.
(When I was playtesting Sokobond, Alan said that I approach puzzles differently to most people. I think I was thinking along the lines of: "okay, the target molecule will only fit here, which means that I need to move into place from there which means…". This kind of thinking comes naturally to me, and I think it serves me well, most of the time - though I have known myself to occasionally prove that this particular level can't possibly have a solution. It seems well-suited to puzzles with predictable mechanics and clear unwinnable states.)
Posted on 20 May 2015
|
Comments
Suppose you and I are farmers, owning adjacent fields. One day you have a brilliant idea. If we dig a ditch from the nearby river, between our fields, then irrigating our fields becomes a lot less work. It would cost two utils to dig the ditch - one utilon each - and we'd get five utils each from its existence.
You come to me with this suggestion. "That sounds great," I say, "but I don't think I'm going to bother."
You object that I'm being dumb not to take those four utils.
"No," I say, "I just think that if I don't help you, you'll do all the work yourself. You still get three utils if you dig it alone, so you'll do it even if I don't help you. And by not helping, I get five utils instead of four. Why would I pay a utilon to help you?"
(Unfortunately for you, I am a member of H. economicus and have a natural immunity to arguments about "fairness" and "not being a douchebag".)
The farmer's dilemma is game-theoretically equivalent to chicken. Both of us choose to either cooperate by digging the ditch ("swerve" in chicken), or defect by sitting at home ("straight" in chicken). If both of us cooperate ("C/C"), we both get an okay result. If both of us defect ("D/D"), we both get a terrible result. If one of us cooperates while the other defects ("C/D"), then the defector gets the best possible result for themselves, and the cooperator gets a result between C/C and D/D.
If you're cooperating and I'm defecting (or vice versa), then neither of us have any incentive to change our strategies. I could start to cooperate, but then I'd just be giving you utility. You'd like that, but I wouldn't. And you could start to defect, but then you'd be throwing away utility. Neither of us would like that.
On the other hand, if we're both cooperating, then we both have an incentive to defect, as long as the other doesn't do the same; and if we're both defecting, we both have an incentive to cooperate, as long as the other doesn't do the same.
(Formally, there are two Nash equilibria, at C/D and at D/C. This distinguishes it from the prisoner's dilemma, which has an equilibrium at D/D.)
There are lots of ways this story can continue.
In one of them, you dig the ditch yourself. Months later, after harvesting and selling your crop, you sit in the pub complaining that being a farmer is such hard work, you've only come out with three utils of profit this year. Nobody's very sympathetic, because they're comparing you to me, and I've made a cool five utils. Because this is a thought experiment, there's no difference between us other than how we act. So obviously you're doing something wrong.
In another possible continuation, you threaten to burn some of my crops if I don't help you dig. Maybe I help you, maybe not; if not, maybe you were bluffing, maybe not; if not, maybe I call the police on you and you go to jail; or maybe I do help you, but I secretly recorded the conversation and leak it to the press later on… a lot of things can happen. Even if this works out great for you, it's at least a little villainous.
Instead of being so blunt, you might choose to convince everyone else to threaten me. Perhaps you dig the ditch, and then talk to our local government and convince them that you should be allowed to extract rent on it.
Another option is to tell me that if I don't help you dig, you'll spend an extra utilon to build a brick wall on my side of the ditch, so that it doesn't do me any good. If I believe that you'll do it, I'm likely to go ahead and help.
You can also tell me that if I don't help, you're not going to dig at all. Or even that you're simply not going to dig, if I'm going to be an asshole about it I can dig the whole thing myself or go without. Once again, I'm likely to dig if I think you're not bluffing.
(Precommitment is a powerful strategy in many situations. But two can play at that game…)
The real world is usually more complicated than game theory. Here are some variations on the farmer's dilemma:
Maybe I have a bad back, and digging is more costly for me than for you. This may or may not change the Nash equilibria, and it may or may not change the amount of sympathy we each get in the various continuations.
Sometimes there are lots of farmers. In this case, the ditch might cost more to dig than the value it provides to any individual, so that nobody will want to dig by themselves; but little enough that you don't need literally everyone to dig before it becomes valuable, so that everyone still wants to defect individually.
Sometimes the ditch might be an agent in its own right. For example, a company might perform R&D only if someone funds them to do so; and everyone wants them to do it, but would prefer that someone else pays.
(They might not have an explicit agreement for funding with anyone, but acausal trade and early adopters and so on.)
(And having developed a super-awesome version of their product, they might also sell a cheaper version, where they've gone out of their way to disable some of the features. This is like building part of a brick wall against people who only contribute a little to the digging.)
Sometimes the ditch might become more valuable if more people help to dig.
Sometimes the ditch requires constant maintenance. We could model that as a sequence of games, where the payoff structure changes between iterations (and might depend on the results of previous games). The ditch might not become profitable until after several rounds.
Why am I talking about this? I think farmer's dilemma situations come up from time to time in online discussions, and I want to be able to say "let's not be too harsh on AcmeCorp here, they're cooperating in a farmer's dilemma and everyone else is benefiting from that". (I don't want to discuss the specific examples I have in mind because they're kind of mind-killey.)
Although the farmer's dilemma and chicken are game-theoretically equivalent, I think our intuitions about them are different. At any rate, mine are. I can think of two reasons for this. One is that game theory only considers utility up to affine transformations. The games "Global thermonuclear war", where every player loses a million utils, and "Global happiness project", where every player gains a hundred utils, are also equivalent. But in the real world, two people crashing their cars into each other is a worse outcome than two people failing to dig a ditch.
The other reason, which is kind of the same reason, is that game theory assumes you've decided to play. If nobody wants to play chicken, you both get a better outcome than C/C. If nobody notices how valuable a ditch would be, you get the same outcome as D/D.
Another equivalent game is the snowdrift dilemma: the road is covered with snow, and we both want it cleared, but we'd both rather not clear it ourselves. My intuitions about this feel different again. You can't decline to play (except by living somewhere less snowy), but if you could, that would be better than C/C.
So describing a situation as chicken, or snowdrift, or a farmer's dilemma, all seem different. I don't know of an existing name that feels like a good fit for the farmer's dilemma. (For a while I thought the farmer's dilemma was a standard name, but I can't find anything about it online. Wikipedia redirects it to the prisoner's dilemma, but that has a very different structure.)
So it seems like a useful concept with no name. Now it has a name. You're welcome.
Posted on 05 May 2015
|
Comments
Sometimes at LW meetups, I'll want to raise a topic for discussion. But we're currently already talking about something, so I'll wait for a lull in the current conversation. But it feels like the duration of lull needed before I can bring up something totally unrelated, is longer than the duration of lull before someone else will bring up something marginally related. And so we can go for a long time, with the topic frequently changing incidentally, but without me ever having a chance to change it deliberately.
Which is fine. I shouldn't expect people to want to talk about something just because I want to talk about it, and it's not as if I find the actual conversation boring. But it's not necessarily optimal. People might in fact want to talk about the same thing as me, and following the path of least resistance in a conversation is unlikely to result in the best possible conversation.
At the last meetup I had two topics that I wanted to raise, and realized that I had no way of raising them, which was a third topic worth raising. So when an interruption occured in the middle of someone's thought - a new person arrived, and we did the "hi, welcome, join us" thing - I jumped in. "Before you start again, I have three things I'd like to talk about at some point, but not now. Carry on." Then he started again, and when that topic was reasonably well-trodden, he prompted me to transition.
Then someone else said that he also had two things he wanted to talk about, and could I just list my topics and then he'd list his? (It turns out that no I couldn't. You can't dangle an interesting train of thought in front of the London LW group and expect them not to follow it. But we did manage to initially discuss them only briefly.)
This worked pretty well. Someone more conversationally assertive than me might have been able to take advantage of a less solid interruption than the one I used. Someone less assertive might not have been able to use that one.
What else could we do to solve this problem?
Someone suggested a hand signal: if you think of something that you'd like to raise for discussion later, make the signal. I don't think this is ideal, because it's not continuous. You make it once, and then it would be easy for people to forget, or just to not notice.
I think what I'm going to do is bring some poker chips to the next meetup. I'll put a bunch in the middle, and if you have a topic that you want to raise at some future point, you take one and put it in front of you. Then if a topic seems to be dying out, someone can say "<person>, what did you want to talk about?"
I guess this still needs at least one person assertive enough to do that. I imagine it would be difficult for me. But the person who wants to raise the topic doesn't need to be assertive, they just need to grab a poker chip. It's a fairly obvious gesture, so probably people will notice, and it's easy to just look and see for a reminder of whether anyone wants to raise anything. (Assuming the table isn't too messy, which might be a problem.)
I don't know how well this will work, but it seems worth experimenting.
(I'll also take a moment to advocate another conversation-signal that we adopted, via CFAR. If someone says something and you want to tell people that you agree with them, instead of saying that out loud, you can just raise your hands a little and wiggle your fingers. Reduces interruptions, gives positive feedback to the speaker, and it's kind of fun.)
Posted on 14 April 2015
|
Comments
Content note: politics, gender politics.
For a while I've been vaguely aware of a petition to "stop taxing periods. Period." I didn't pay it much attention until today, but now I've looked at it and done way more research than I expected to.
According to the petition,
A 5 per cent tax rate has been placed on sanitary products, while exotic meats walk tax-free. HM Revenue and Customs justified this tax by classifying sanitary products as "non-essential, luxury" items.
At least the first sentence of this is true. Sanitary products have VAT of 5% imposed on them. Exotic meats (including horse, ostrich, crocodile and kangaroo) do not.
Sanitary products are covered by VAT notice 701/18, which reduces the rate on them from the standard rate (currently 20%) to 5%. It applies only to "any sanitary protection product that is designed and marketed solely for the absorption or collection of menstrual flow or lochia (discharge from the womb following childbirth)". That is, this reduction was introduced specifically to reduce tax on sanitary products.
Exotic meats are covered by 701/14, which covers food in general. Most food is zero-rated. There are further exceptions for some things, including chocolate covered biscuits (but not chocolate chip biscuits), which are standard-rated; exotic meats are not one of those things. What seems to have happened here is that the government decided that most food should be zero-rated, and then made a list of foods that shouldn't, and exotic meats didn't happen to make it on to the second list for whatever reason.
I'm less sure about the second sentence, HM Revenue and Customs justified this tax by classifying sanitary products as "non-essential, luxury" items. More from the petition:
After the UK joined the Common Market in 1973, a 17.5% sanitary tax was introduced. It was justified when Parliament classified sanitary products as "non-essential, luxury" items.
I don't think this is true, but I think I can see how the story could have been chinese-whispered into existence:
- When the UK joined the Common Market in 1973, we introduced VAT. The standard rate of VAT used to be 17.5%.
- My current belief is that until 2000 or 2001, sanitary products were standard-rated. It's not that there was a specific "sanitary tax", but VAT was a tax that applied to sanitary products.
- It seems to be widely assumed that VAT exemptions are given to essential items, and not to others. Since sanitary products were standard-rated, they must not have been considered essential, so they must have been considered luxury.
But: In 1973, the standard rate of VAT was 10%. I'd be very surprised if sanitary products were taxed at 17.5% in 1973.
VAT actually replaced purchase tax, which did only apply to luxury goods. So if sanitary products were taxed for the first time in 1973, it's because they weren't considered luxury.
Putting "non-essential, luxury" in quotes would seem to imply that this is a direct quote from something, but the first page of google results for that page all seems to be inspired by the petition at hand. The second page has nothing helpful, the third is back to this petition. I haven't found a source for this phrase.
In fact, I haven't found any official source that suggests that the government thinks sanitary products are non-essential. The evidence for this seems to be purely the fact that they have 5% VAT imposed on them.
But this assumes that VAT is not applied to essential products, which as far as I can tell just isn't true. Here is the entirety of the official-seeming evidence I've found which connects essential-ness to VAT status: a page on gov.uk which says "You pay 20% VAT most of the time - but less on essential items."
One reading of this is that all essential items, and only essential items, are taxed at less than 20%. By this reading, sanitary products are essential, being taxed at 5%.
On the other hand, when you look at the list of VAT exemptions, it includes gambling and antiques, which seem pretty non-essential; and it doesn't include clothes for adults, which are pretty damn essential. (If I don't wear clothes, I will get locked up. I'm forced to pay tax on the clothes that I'm forced to wear. This is almost Kafkaesque, in a really really minor way.)
Just in the healthcare genre, it doesn't include toothpaste or dental floss, most glasses or hearing aids, sticking plasters, paracetamol, or the creams I use for acne and eczema. (I haven't specifically researched most of these. I think I've looked in the places where I would find them if they were covered, but it's possible I've made a mistake.)
It does seem that most of the things in that list are things that most people think should be easily accessible. But if I showed someone that list without telling them what it was, I don't think they'd say "this is a list of things which are essential".
Wikipedia also doesn't use the word "essential".
If we ignore that one linked page, it just doesn't seem like the government classifies things as essential or not, and then assigns them a VAT status based on that classification. It just assigns VAT status. To ask whether the government considers something "essential" seems to be asking a null question. That's not a word that the government, as a body, knows.
There is still that one linked page, but currently I'm dismissing it as an anomaly. Gov.uk is intended to be accessible and accurate, and in this case I suspect that accessibility triumphed over accuracy, and/or someone just made a mistake while writing it.
I worry that I'm simply ignoring contarary evidence here, but consider: the government publishes a list of things. It doesn't put things on the list just for being essential, or deny them from the list for being nonessential. It doesn't correlate very well with what most people would consider essential. I can only find one place where the government comes close to describing it as a list of essential things, and that's in a descriptive context, not a binding one.
If it doesn't look like a duck, quack like a duck, or fly like a duck…
So. In 1973, the government probably did not consider sanitary products to be "non-essential, luxury" items. It just considered them to be things, and it taxed them the same as it taxed most things.
Since 2001, the government almost certainly doesn't consider sanitary products to be non-essential. It taxes them at a reduced rate compared to almost everything else, but at a higher rate than some other things.
Under EU law, the government isn't allowed to zero-rate them. We have other zero-rated things, but they were zero-rated before we joined the EU. The VAT on sanitary products is as low as it is permitted to be.
We might (or, quite likely, might not) be able to exempt sanitary products instead of zero-rating them. But there's an important difference. If you buy raw materials, produce a product, sell it, and have to pay VAT on the sale, then you can claim back the VAT that your supplier paid on the materials. If you don't pay VAT on the sale, you can't claim back that VAT. If sanitary products were exempt rather than not zero-rated, the selling price might (or might not) go up because of this, depending on the cost of raw materials. It's almost certainly more complicated than this, but:
Suppose you buy £30 worth of cloth, of which £6 is VAT. You make a lot of tampons and sell them for £100. You have to pay £5 VAT on that sale, and can claim back the £6 VAT you paid on the cloth. Profit: £100 - £30 - £5 + £6 = £71. If tampons were VAT exempt, you'd need to sell them for £101 to make the same profit.
(The past two paragraphs were written from the perspective that the seller pays VAT. Mostly we seem to talk about the buyer paying VAT. It's all equivalent, but I hope I wasn't too confusing.)
Having established (what I believe to be) the facts, here are my thoughts on the petition itself:
Firstly, it doesn't strike me as a particularly big deal.
Financially, we're talking about £150 a lifetime lost to taxation on sanitary products, assuming £5/month for 50 years. I don't think anyone is claiming it's a particularly heavy burden, it's not about money.
From a gender-politics perspective… it also just doesn't seem like a big deal. If sanitary products were still standard-rated, I could maybe kind of get behind this, even though I don't actually think that standard-rated implies non-essential. But they're at the lowest VAT rate the UK government is allowed to put them at. I just don't see this as a sign that we value crocodile meat more than female participation; or of male-focused agenda setting; or any form of institutional misogyny.
It seems like most of the conversation is fueled by outrage. I don't think there's much here to be outraged about, and I would prefer that the energy being put into this outrage goes elsewhere.
Secondly, I don't really like the tactic of petitioning the UK government over this. The petition acknowledges that they can't do anything under current EU law. So the goal is to get the UK to get the EU to change its laws.
That seems… really unfair. I don't think I can argue clearly and succinctly for that position, which usually means I should spend more time clarifying my thoughts to myself. Instead of doing that, I'm going to argue by analogy. I don't think these analogies are the same in every way, or even in every relevant way; they just seem to me to have some structural similarities to the case at hand.
So, suppose I notice that I've been overcharged on my phone bill. I call up the company, and the customer service rep is very polite and helpful and refunds me. I tell her, "that's not good enough, I also want to be refunded for the price of this phone call to you, that I shouldn't have had to make". She tells me that she simply doesn't have the power to do that. So I tell her that she needs to complain to her managers until they give her that power, and I'm going to keep calling her every day until she can refund me for the cost of this phone call.
This isn't her battle. She's sympathetic to my plight, but she has other priorities. And I'm blackmailing her into fighting for me.
This feels kind of like that kind of power dynamic.
Or: "hey man, I just need 20p for my bus fair, can you help?" "Sorry, I'd like to, but I have nothing smaller than a tenner." "So give me a tenner, don't be a tightass."
There's only so far that you can expect someone to go for you, and I feel like this petition is asking for more than that.
Posted on 22 February 2015
|
Comments
It's widely regarded that documentation is an important task that doesn't get as much attention as it deserves.
There are a lot of proposals for how to fix this, but I think they typcially miss something. "Write the documentation before the code", for example. Sounds good, but a lot of the time, until I write the code, I don't know what it's going to do. Maybe I have a rough idea, but the details are going to evolve. And sometimes I'm just going to get things wrong. Oh, I can't frobnicate the spam here unless I also make the user pass in an egg - this is the sort of detail that would be easy to miss when I'm thinking about a function, but impossible to miss when I'm trying to frobnicate the spam without an egg.
And of course, having written a function and documented it (in whatever order) - you can subsequently rewrite the function without redocumenting it. This is the well-known problem where the code and the docs get out of sync.
You can't have a rule "don't edit the code unless you first edit the documentation", because a lot of code edits don't need doc changes. A more complicated rule like "don't edit the code unless you first edit the documentation, unless the documentation doesn't change" would probably just be forgotten. After a while, whenever I ask myself if the documentation is going to change, I'm just going to return the cached answer "no" without thinking. In any case it has the same problem: I don't know what I'm going to change until I change it.
So here's my half-baked proposal that might help to solve some of the problem of keeping code in sync with documentation:
If your code is in a git (or other VCS) repository, you can look at a function and see whether the code changed more or less recently than the docstring. It would be possible to write a tool which searches for such functions automatically.
Bam, done. The rest is just details. Edit code all you want, and if you forget to update the docs, this tool will remind you next time you run it.
Okay, some details are important. Here are some things to think about:
-
Not every code edit needs you to touch the docstring, so you want a database of some sort, which can be used to mark "the docstring is up to date as of commit A, even though it hasn't been touched since commit B". Keep this database inside your repository. This is probably quite a large detail, with many details of its own.
It might actually be better (certainly simpler) to have some way of marking this in-file. For example, in python:
def foo(bar):
"""Do a thing
""" # 2014-01-07 11:25 (edit this comment to mark the docs up to date)
pass
-
Tracking a function across revision changes is probably really hard, in general. In the specific case of "the sort of revision changes that actually occur in real codebases", it might be possible most of the time.
((I would start by working out which lines constitute a function's code and docstring, and running git blame to see which was updated most recently. This might be good enough, but for example it breaks if you swap the order of two functions in the source file. One of them is going to be blamed entirely on that commit. It also breaks if you delete lines from the function body.
A more complicated solution would be to track the function by its identifier. Look at past revisions of the file in its entirety, search for the function, and see whether it's changed. This could go wrong in so many ways, and even if it doesn't, it still won't catch you if you move a function from one file to another.))
-
This probably works best if you run it frequently. You could have it in a hook: if there are unsynced changes, you aren't allowed to push unless you sync them (either by editing the docs, or marking them clean).
-
This could be applied to classes as well as functions, but I'm not sure when you'd want to flag them. Most changes to code inside a method probably won't touch the class docstring, even if they touch the method docstring. Applying it to whole files would be even harder. In general, this will apply better to low-level documentation than high-level.
-
You need custom support for each language and documentation style used, as well as for each VCS. In many cases, supporting a language will mean writing a parser for it. (In python, you can import a module and discover every class and function that it exposes, and their docstrings, but I don't know if you can find their source locations like that.)
Would this work? How much effort would it be to make? Would it be helpful, assuming it did work? For that matter, does something like it already exist?
Posted on 16 January 2015
|
Comments
In which I inexpertly channel Randall Munroe
Soon the seas will turn red with the blood of the human race, as the unspeakable terrors come from beyond the gate, which is Yog Sothoth, to devour all in their path! Ia! Shub Niggurath! Ia! Ia!
— Who will be eaten first?
If you were to mix the blood of the human race into the oceans, how red would they turn?
A quick fermi estimate: there are seven billion humans, with about eight pints of blood each, which is about five litres. So we have about 35 billion litres of blood to work with.
How about the oceans? They cover two thirds of the earth's surface. I know that the surface of the earth is $4πr^2$ where $r$ is 6,400 km. $(64 × 10^5)^2 = 2^{12} × 10^{10} = 4096 × 10^{10}$. $4π$ is approximately ten, so the surface area of the earth is about $4×10^{14}$ m². Two thirds of that is $2.5 × 10^{14}$. I don't know how deep they are, but 100m seems like a reasonable guess at an average. That gives us about $2.5 × 10^{16}$ m³ of ocean.
A cubic metre is a thousand litres, so we have about 25 billion billion litres of ocean. For every drop of blood, we have almost ten billion drops of ocean.
I don't know how blood and water mix, but I'm confident that the oceans will not be running red with blood any time soon, on average. Sorry cultists.
Fact checking: Wolfram Alpha tells me that there are actually about 10¹⁸ m³ of ocean, which is 40 times what I guessed, which is okay for a Fermi estimate. The oceans are still not running red with blood.
NOAA, whoever they are, tell me that the average depth of the ocean is 4km, which is also 40 times what I guessed. That's not great for a Fermi input.
(Initially, I forgot the $4π$ factor in the surface area of the earth, putting me off by 400 times. I'm not sure how to judge myself on Fermi estimates when I get somewhat-reasonable inputs and do the math wrong.)
However! The quote specifically mentioned seas. I've cheated by counting oceans as seas. What if we exclude them? I'm going to do this just by listing the oceans and subtracting their volume from the total. We have:
It's possible that this double-counts the Southern ocean, since some people divide it up between the Pacific, Atlantic and Indian oceans. But I'm going to allow that, to make the seas as small as possible.
In total, this makes $1.29 × 10^{21}$ L of ocean. That's more than the $10^{18}$ m³ I gave earlier, but that was rounded. The actual number given is $1.332 × 10^{21}$ L. So there are $0.042 × 10^{21} ≈ 4 × 10^{19}$ L of seas in the world. This is actually pretty close to my initial guess for the oceans. Still no red.
This does not mean you are safe from the Elder Gods.
Posted on 09 August 2014
|
Comments
I like Python, but one of the things I dislike is the assert statement. Its simplest form provides no help if it fails:
will raise an exception so you can see where it failed, but you don't get to see what x or y were.
There's a longer form,
assert x == y, "%r != %r" % (x,y)
but this is verbose, and evaluates x and y twice. And if x and y are dictionaries nested three deep, it might not be easy to tell what's different between them.
I'm aware of two approaches that improve the situation. nose has a --failure-detail plugin that tries to automatically give you more detail. When
fails, it:
- Finds the source location of the failed assert,
- Reads and parses this line,
- Substitutes variables with their values,
- Reports the substituted line.
This is an awesome hack, and I love that it's possible, but I don't find it all that useful. You still need to play spot-the-difference with deeply nested data structures, but that would be pretty easy to fix. The deeper problem is that it also doesn't help with
assert frobnicate(3) == frobnicate(4)
because there are no variables to replace. (frobnicate is a variable, but IIRC it doesn't substitute functions. I don't remember the exact algorithm it uses.) I had a look at the code, and I don't think it would be possible, in general, to report the values on the LHS and RHS. You'd have to re-evaluate the expressions, and there's no guarantee they'd return the same thing the second time.
The second approach is to get rid of assert statements completely. In a unittest test, you do
and if x != y it tells you what x and y are, with a helpful diff format for dicts, lists and sets.
This is great, but I just don't like writing asserts like that. So here's a new approach:
from bsert import bsert
bsert | x == y
How it works is that bsert | x returns a new object, _Wrapped(x); and _Wrapped(x) == y calls assertEqual(x, y). Other comparison methods are overloaded as well. Now we can do things like:
$ python
Python 2.7.5 (default, Dec 1 2013, 00:22:45)
[GCC 4.7.3] on linux2
Type "help", "copyright", "credits" or "license" for more information.
>>> from bsert import bsert
>>> bsert | 3 == 3
True
>>> bsert | 3 == 4
Traceback (most recent call last):
...
AssertionError: 3 != 4
>>> bsert | [3] + [4] == [3, 4]
True
>>> bsert | [3] + [4] == [3, 4, 5]
Traceback (most recent call last):
...
AssertionError: Lists differ: [3, 4] != [3, 4, 5]
Second list contains 1 additional elements.
First extra element 2:
5
- [3, 4]
+ [3, 4, 5]
? +++
>>> bsert | {1: {2: 3, 4: 5}, 6: 7} == {1: {2: 4, 4: 5}, 6: 7}
Traceback (most recent call last):
...
AssertionError: {1: {2: 3, 4: 5}, 6: 7} != {1: {2: 4, 4: 5}, 6: 7}
- {1: {2: 3, 4: 5}, 6: 7}
? ^
+ {1: {2: 4, 4: 5}, 6: 7}
? ^
>>> bsert | 1 / 2 != 0
Traceback (most recent call last):
...
AssertionError: 0 == 0
>>> bsert | 1.0 / 2 != 0
True
>>> import time
>>> bsert | time.time() != time.time()
True
>>> bsert | time.time() == time.time()
Traceback (most recent call last):
...
AssertionError: 1399731667.416066 != 1399731667.416123
>>> bsert | [3] * 3 == [3,3,3]
True
>>> bsert | {1, 2, 3} <= { 1,2,3,4}
True
>>> bsert | {1, 2, 3} >= { 1,2,3,4}
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
File "bsert.py", line 28, in __ge__
self.assertGreaterEqual(self.wrapped, other)
File "/usr/lib64/python2.7/unittest/case.py", line 950, in assertGreaterEqual
self.fail(self._formatMessage(msg, standardMsg))
File "/usr/lib64/python2.7/unittest/case.py", line 412, in fail
raise self.failureException(msg)
AssertionError: set([1, 2, 3]) not greater than or equal to set([1, 2, 3, 4])
>>> bsert | 3|8 == 11
True
>>>
There are a few limitations. For one, you can't use chained comparisons, and you won't get any kind of error if you try. The reason is that
cashes out as
(bsert | 3 <= 5) and (5 <= 4)
so there's no way for bsert to know that there's another comparison going on. For two, you can't do
because there's no way to overload the in operator from the left hand side. (In this case, you at least get an AssertionError: 1 != 3 telling you you did something wrong, because a in someList basially does any(a == x for x in someList), and so it fails at bsert | 3 == 1. If you had a dict, set, or empty list on the right hand side, it would just return False and not raise an exception.)
Similarly, bsert | x is y, bsert | x and y and bsert | x or y don't work, because those operators can't be overridden at all. (Even if they did work, they're low precedence, so it would need to be e.g. (bsert | x) and y, which is horrible.) You also can't do
because that just returns _Wrapped(False)
I think all the other operators should work fine, if you're using them in ways that make sense. Most of them have higher-precedence than |, so that for example
cashes out to
The only exception is | itself, and I've added support so that _Wrapped(x) | y returns _Wrapped(x|y).
I don't necessarily recommend that you use bsert. I'm not sure that I will. But it's there.
I've put bsert on github, but it's also short enough that I might as well just post it inline:
import unittest
class _Bsert(object):
def __or__(self, other):
return _Wrapped(other)
class _Wrapped(unittest.TestCase):
def __init__(self, obj):
# TestCase needs to be passed the name of one of its methods. I'm not
# really sure why.
super(_Wrapped, self).__init__('__init__')
self.wrapped = obj
def __eq__(self, other):
self.assertEqual(self.wrapped, other)
return True
def __ne__(self, other):
self.assertNotEqual(self.wrapped, other)
return True
def __le__(self, other):
self.assertLessEqual(self.wrapped, other)
return True
def __ge__(self, other):
self.assertGreaterEqual(self.wrapped, other)
return True
def __lt__(self, other):
self.assertLess(self.wrapped, other)
return True
def __gt__(self, other):
self.assertGreater(self.wrapped, other)
return True
def __or__(self, other):
return _Wrapped(self.wrapped | other)
bsert = _Bsert()
Belated update:
On reddit, Liorithiel informs me that py.test can extract useful failure messages from assert statements. Like what nose does, but implemented differently, so that it can show the values of intermediate expressions in more detail than bsert can. (It rewrites the AST on import time, which is an even more awesome hack than nose's.) As far as I'm concerned, this knowledge makes bsert obsolete.
Meanwhile, obeleh on github has provided a patch which allows bsert to be used with boolean expressions, with different syntax. So
is like assert 3 in [1,2,3], but with a slightly nicer exception message. (The old syntax still applies for expressions using comparison operators.) Now you get
AssertionError: bsert(3 in [1,2,3])
instead of just
It comes at the cost of a slightly longer traceback - I wonder if that can be worked around. And it doesn't provide intermediate expressions at all, so it's kind of a neat trick, but I don't know if it's useful. (Especially since the old traceback had the failing expression near the bottom anyway - there are cases where you'll see the exception but not the traceback, but we're getting into niche territory.) But that's pretty much how I felt about bsert in the first place, so I decided to go ahead and include it.
Posted on 10 May 2014
|
Comments
I don't expect anyone cares about what I think about the movies I've seen lately, so I'm bundling those thoughts into one post to be less annoying.
The Lego Movie
This is the most pure fun I've had watching a movie in a long time. It's going for funny, and it is, the whole way through. As I write this, I saw the movie almost a month ago, and remembering some of the jokes still makes me smile.
The attention to detail is also impressive. I think that if I rewatched this, I'd catch a bunch of stuff that I missed the first time. Going frame-by-frame would help at times.
Highly recommended.
Divergent
I found Divergent decent while watching it, but no more than that; and thinking about it afterwards only makes it worse.
It's pretending to be a failed-utopia story: at some point in the past, someone came up with a really dumb idea ("let's end conflict by separating everyone into five factions based on personality traits!") and apparently society rolled with it. Now the heroine, along with the audience, learns that it's a really dumb idea ("oh hey, it turns out that some people have more than one personality trait, guess we'll have to kill them"). So far, so Gattaca.
But in this case, just in case you weren't convinced that the faction idea was dumb, you get to see what happens when the faction system meets mind-control drugs. The answer is "pretty much what happens when mind-control drugs enter any society", but because it's happening to the faction system, it's the faction system that looks bad.
There's also a sort of Mary-Sue thing going on, but a viewer insert rather than an author insert. In the film world, people supposedly have only one of the traits brave/honest/friendly/selfless/clever, except for the rare divergents. So the message is "if you have two or more of these traits, you are rare and special and immune to mind-control drugs, and people will hate you for it", which is probably a message that will appeal to angsty teenagers.
Captain America: The Winter Soldier
This is an action film. It has people shooting people, and punching people, and jumping through glass windows. I have it on good authority that a lot of people enjoy that sort of thing.
There's a political-thriller plot in there, as well, but not a particularly interesting one. Director Fury recommends delaying the project to create a doomsday device that will only be used to kill bad people. Director Fury can't be trusted, because he recently hired a merc to hijack a ship owned by SHIELD (I never quite worked out why he did this). Also, someone has just killed Director Fury. Full speed ahead on the doomsday project!
There's the standard trope that when things seem hopeless for the heros, we find out that they set things up in advance to control for this very circumstance. And the same with the villains. This keeps the tension high, or something.
Brain uploads are possible, and have been possible since the seventies or so, but no one really cares, and only one person has been uploaded. The upload commits suicide to try to kill the heros, where any normal villain would have an escape plan, or at least some lines about how he's giving his life in the service of Evil; we don't get that here, because people aren't people unless they're made out of meat. (Actually, I assume that the Marvel universe has many people who aren't made of meat, but are still given personhood-status. Maybe the rule is "unless they look like us, except that they're allowed to be a different color"?)
(There's a similar thing with cryonics, but it's not clear whether normal humans can be suspended and revived, or just superhumans.)
The Winter Soldier thing feels tacked on. He's an assassin who is approximately as good at fighting as the hero is. It also turns out he's the hero's brainwashed childhood friend, returning from the first movie. The hero gets kind of sad about this, but they fight anyway. In the end, the Soldier saves the hero's life, but he only gets to do it because the hero was trying to save his life, and they don't have a big moment of reconcilliation, it just kind of happens. I guess the idea is to set something up for the third movie, but in this one, there was no reason that character couldn't have just been someone new, or even completely removed from the film.
Really though, I think the main thing I'd like to change about the film is: to a first approxmation, nobody gets hurt. People fight, and everyone who isn't a named character dies, and the named characters don't have a scratch on them despite getting repeatedly punched in the face. I know some people enjoy watching this, but I find it kind of boring, and I think that if we saw the hero sustain a split lip and a bloody nose, I might find it a lot more engaging because suddenly it might feel like he's actually in danger. (I can forgive that people don't get cut when they crash through glass windows. If they did, they would be a lot less willing to keep doing it.)
Of course, this film is only a 12A. If you show people getting hurt in fights, kids might not be allowed to watch it any more.
I did like how there was no romantic subplot.
Also, faceblind world problems: a minor character suddenly unleashes some ass kicking. Everyone looks at her like wtf. She presses a button, her face shimmers as a hologram disappears, and suddenly she looks exactly the same. (She then proceeds to remove her wig, so it's not too confusing.)
Noah
Everybody in this film fails ethics and/or metaethics forever.
Spoilers ahead, even if you've read the Bible. I can't be bothered to mark them all.
Noah thinks the world would be better off if all the people were dead, including himself and his family. He thinks his task is to save the animals and then to die.
I can accept the hypothesis that the rest of the world is evil. It's a stretch, but I think we don't see anyone outside Noah's family do anything good, so let's roll with it, and say that sure, they deserve to die.
What about Noah and his family? He explains this to his wife, Naameh, pointing out their flaws to her. Their youngest son, Japheth, seeks only to please. Or something like that. I agree that that's a character flaw, but if it's the worst you can say about someone, they're a pretty good person. I don't remember what he said about Shem and Ham - I think maybe Shem's flaw was being sexually attracted to his girlfriend Ila (in Shem's defence, Emma Watson), and Ham wanted a girlfriend too much - but it definitely wasn't "deserves to die" grade stuff. And Noah and Naameh would both kill to protect the children, which apparently makes them just like everybody else.
I'm not being entirely fair. The world is beautiful, humans ruined it once, and however good Japheth may be, we can't trust that his kids will be as good as him, and their kids will be as good as them, and so on. We can turn this into a parable about AI safety and the Löbian monster, but I don't think that was the intent.
Okay, fine. Humans need to die off. That's not Noah's problem. Noah's problem isn't even necessarily that he thinks God is talking to him, because that does happen. I'm not sure I can pinpoint exactly what Noah's problem is. Maybe it's that he seems to think that he and he alone is vital to God's plans.
When Ham tells Noah that he wants a wife, Noah tells Ham that God will provide everything they need. Later Noah goes to look for a wife for Ham. When he fails, he decides that God doesn't want Ham to have a wife, and that's when he works out that his family isn't meant to repopulate the Earth. When Ham finds a wife for himself (well, a scared lonely little girl, but in those days, what was the difference?), Noah abandons her to die.
Noah's thought process seems to be: if God wants something to happen, He will do it himself or He will work through Noah. So when Methuselah blesses Ila, and Ila subsequently becomes pregnant, the idea that this might have been God's will doesn't cross Noah's mind, and he proclaims that if the child is a girl (capable of repopulating the Earth), he will kill her.
(Incidentally, Methuselah blesses Ila when Ila is looking for Ham, who needs to be found fairly urgently. Their conversation wastes minutes, and after he blesses her, she goes and finds Shem - also looking for Ham - for making out, leading to an implied offscreen shag. Ham is forgotten.)
This brings us to the problem that most of the other characters share: they are far too passive. No one apart from Noah is cool with the human race dying off, but when Noah announces his plans, they don't do very much about it. Naameh tells him that if he kills the child, she will hate him. Japheth sends out one bird at a time to try to find land before Ila gives birth, maybe so that they can run away from Noah? Shem and Ila build a small raft, with food for a month, and plan to desert the Ark. But they neglect to make any secret of this, and when Noah burns it, they're surprised.
I am probably a little too quick to say that fictional characters should be killed, in circumstances where that wouldn't fly in the real world. But in fiction, the stakes tend to be a lot higher. In this case, the stakes are the survival of the human race. The obvious thing to do is to kill Noah.
Don't run away on a raft. The Ark is safer. You are the last hope for the human race. Kill Noah.
When Noah has attempted to kill your children, and discovered that he can't do it, kill him anyway. He hasn't changed his mind about what God wants, he just thinks he's failed God, and do you trust him not to try again? Kill him. (Eventually, Noah does change his mind, when Ila suggests that maybe God deliberately left the choice to Noah. Now Noah believes he's not only vital to God's plans, but is permitted to shape them.)
Well, Shem eventually makes a cursory attempt, at least. But it's not good enough. NPCs, the lot of them.
There are two more characters. Tubal-Cain is the villain. He thinks that man should have dominion over nature. He also decides that since God has forsaken them, so much for ethics, and he'll kill anyone he wants.
Ham is the only one of Noah's sons to express any independence. His motivation is that he wants a wife. When Noah fails to find him one, he goes to find one himself. He rescues a girl from the human settlement, they run away back to the Ark together, and when she gets caught in a bear trap with the bad guys in hot pursuit, he tries to save her. Noah arrives to save him, and he trusts Noah to save her as well, which he doesn't.
When Tubal-Cain breaks on to the Ark, Ham finds him and becomes his protégé. Sort of like Anakin Skywalker being turned against the Jedi Council by Senator Palpatine. But when it comes down to it, Tubal-Cain and Noah are fighting, and Ham decides to kill Tubal-Cain instead. (At this point, Tubal-Cain tells Ham, he has become a man. Tubal-Cain returns the magical glowing snakeskin that he took when he killed Noah's father. It's the skin shed by the snake that tempted Eve. It's all very significant, presumably, but I don't know what it signifies.)
Meanwhile, God is classic Old Testament God. He's not very communicative, which causes Noah no end of confusion; He only ever intervenes at the last minute, because He loves a fight scene as much as the rest of us; and apparently "flood the world" was the best plan He could come up with for making everything cool again.
Apart from all the ethics, the film is still pretty bad. The script is uninspired. Tubal-Cain gets some villainous monologues and a rousing pre-battle speech, but they pretty much consist of him talking about how much killing he's going to do. I did enjoy the visuals, and Russell Crowe and Emma Watson do the best they can.
I do not recommend Noah.
Ocho Apellidos Vascos (Eight Basque Surnames / Spanish Affairs)
This reminded me a lot of Intouchables. That was a French feelgood comedy-drama which ended up making a lot of money. This is a Spanish feelgood romcom which is making a lot of money. Both are heavily based on the cultural divide between the main characters. Both are well-made, but very paint-by-numbers.
Apellidos features the boy and the girl meeting. The boy thinking there's something Special between them. The girl disagreeing. The two of them getting up to crazy antics. The girl changing her mind. The boy rejecting her, and then changing his mind. The assumption that these people, who first met a week ago, and now think they're in love, will live happily ever after.
In this case, the boy is Andalusian, and the girl is Basque. I don't know much about Spanish politics, and the film doesn't go out of its way to explain (why would it?), but I get the impression that there's a great deal of tension between the Basque people and everyone else in Spain; much like Northern Ireland and the rest of the UK, back in the days when the IRA was bombing pubs and cars and stuff (okay, I don't know too much about local politics either). Accordingly, just about every character in the film is incredibly casually racist. Sometimes that's played for laughs, and probably exaggerated; other times it seems entirely plausible. It was kind of distracting: I kept thinking there is no way you could show this if you substituted Basque for Black. But then, maybe you could if you went for Irish instead.
I found the subtitles hard to follow at times. There were some words which weren't translated (I think maybe these were spoken in the Basque language), and they were easy enough to pick up but required slightly more effort than normal. And there were a number of references to things I'm not familiar with, which I had to piece together from context; again, not difficult to do, but not effortless.
Mostly, I thought this film was funny, sweet, and forgettable.
Posted on 19 April 2014
|
Comments
I'm a fan of the board/card game The Resistance, but I feel like the base game is significantly unbalanced in favour of the spies. I think that if the spies play well, they will usually win regardless of how well the resistance plays; and I think that playing well simply involves not acting like spies. (To be precise, I think that if the spies always act in public the way they would if they weren't spies, the game becomes very easy for them; they don't need to execute complicated plots to try to throw suspicion on an innocent, and they don't need to subtly communicate with each other about which of them is going to throw a failure card down on this mission. This isn't necessarily easy for them, but it's fairly simple in principle, and I expect it becomes easier with practice.)
To test this, I intend to analyse a similar, simpler game which I call Resistance-B. "B" for "brainwashed", because in this game the spies don't know they're spies, and they don't know who the other spies are either. However, any time they go on a mission, their programming takes over and they sabotage it without knowing what they're doing. If there are multiple spies on a mission, they all sabotage it.
This probably wouldn't be very fun to actually play as a group (and you'd need a GM, or some other way to find out how many spies were on a mission without the spies themselves knowing). But it seems clear that, provided all players are good at acting, this is a variant which is strictly harder for the spies to win. Their strategy in this game is available in plain Resistance (always act like a resistance member in public, but sabotage all missions), but some options have been removed, and the resistance members know that this is their strategy.
This game is also a lot easier to analyse than the original. Everyone has the same information, so there's no need to vote on teams. In fact, we can think of it as a one-player game against a random opponent; all the opponent does is pick the spies, and the player needs to pick teams to execute three successful missions.
My hypothesis is that for many game sizes, the spies will have considerably greater than even odds of winning. To be less vague, I expect the spies to have a disadvantage in five-player games at least1, but for six I'm not sure which way it would go, and by eight I expect the spies to be usually winning. (I also expect the game generally gets harder for the resistance as you add players, except that nine players is obviously easier than eight. Having one more exception wouldn't surprise me much, but two would. (If ten is easier than eight, that doesn't count as an exception, because ten is clearly harder than nine. However, it would also surprise me a little if ten was easier than eight.))
1. Although I don't remember specifically predicting this prior to beginning the analysis below. I got as far as "40% of the time, the resistance wins just based on the first round" before I started to write this post.
Note that if I'm wrong, that doesn't mean the original Resistance is unbalanced, although it's evidence against it (strength depending on just how badly wrong I am); but if I'm right, the Resistance certainly is unbalanced.
For people not familiar with the original game, here are the rules of Resistance-B. You have a specified number of players2, some of whom are "resistance members" (good guys) and some of whom are "government spies" (bad guys). A third of the players, rounded up, are spies, but you don't know which. The game progresses in up-to-five rounds. In each round, you select a specified number of your players, and find out how many of them were spies. If none of them were spies, you win that round. If any of them were spies, you loose that round. Your goal is to win three rounds. The number of players selected in each round depends on the total number of players, and the round number (the table is given on wikipedia). In addition, for seven players and up, you win round four unless you select two or more spies, not one or more.
2. The way I'm presenting the game, these aren't real players. You are "the player", and the game contains fictional players whom you control.
Resistance-B is easy to analyse case-by-case for five players (three resistance, two spies). With no information, we select the starting team (two players) randomly. There are three equivalence classes of outcomes:
- No spies ($p = { 3 \choose 2 } / { 5 \choose 2 } = 0.3$). In this case, the resistance always wins. Mission three also only takes two members, so it's a guaranteed success. On each of missions 2, 4 and 5, take one of the remaining players until you find the one who isn't a spy.
- Two spies ($p = 1 / { 5 \choose 2 } = 0.1$). Now we know exactly who the spies are. Easy win.
- One spy ($p = 0.6$, by elimination). We have players A through E, and precisely one of A and B is a spy, and precisely one of C, D, E is a spy. For mission two, our choices are (wlog) ABC and ACD. (CDE is stupid, because we gain no information and are guaranteed the mission will fail).
- ABC is a guaranteed fail, but
- If we get two failure cards ($p = 1/3$), we know C is a spy. We can't afford to fail any more missions, and we can't distinguish between A and B. So we send AD on mission 3; if it succeds ($p = 1/2$) we win, if it fails ($p = 1/2$) we lose.
- If we get one failure card ($p = 2/3$), we know C is not a spy. One of AB, and one of DE, is a spy; we can't afford to send any more spies on missions, so we have a $1/4$ chance of winning.
So ABC gives us a $1/3$ chance of winning.
- ACD has a ${1 \over 2} \cdot {1 \over 3} = 1/6$ chance of succeding, but if it does we know who the spies are and win. It has a ${1 \over 2} \cdot {2 \over 3} = 1/3$ chance of getting two failure cards; now we know BE are good, A is bad, and have a 50/50 chance of selecting between CD to win. And there's a $1/2$ chance of getting one failure card.
In this case, $1/3$ of the time, AE are spies and BCD are not. $2/3$ of the time, the spies are B and one of CD. Again, we can't afford to fail any more missions. So we can choose either BCD or ACE to go on the remaining missions, and we'll have a $1/3$ chance of winning.
So ACD has a ${1 \over 6} + \left({1 \over 3} \cdot {1 \over 2}\right) + \left({1 \over 2} \cdot {1 \over 3}\right) = 1/2$ chance of winning.
So if there's one spy amongst AB, we select team ACD for mission two, and win half the time.
In total then, we win the five-player game 70% of the time. That's not surprising.
The six-player analysis could probably be done analagously without too much trouble, since there are still only two spies. But the mission sizes go 2-3-4-3-4, which means that if we select no spies in the first mission, it's not obvious that we win, and if we select one spy we also have the choice of selecting CDE for mission two… the decision tree gets a lot more complicated, and I'd rather try to solve this problem intelligently (to work for game sizes 7+ as well). I haven't done this yet, though; it's a job for future-me.
Posted on 29 March 2014
|
Comments
 A photo from a (different) recent LW London meetup
A photo from a (different) recent LW London meetup
Cross-posted to LessWrong
I wasn't going to bother writing this up, but then I remembered it's important to publish negative results.
LessWrong London played a few rounds of paranoid debating at our meetup on 02/02/14. I'm not sure we got too much from the experience, except that it was fun. (I enjoyed it, at any rate.)
There were nine of us, which was unwieldy, so we split into two groups. Our first questions probably weren't very good: we wanted the height of the third-highest mountain in the world, and the length of the third-longest river. (The groups had different questions so that someone on the other group could verify that the answer was well-defined and easy to discover. I had intended to ask "tallness of the third-tallest mountain", but the wikipedia page I found sorted by height, so I went with that.)
I was on the "river" question, and we did pretty badly. None of us really knew what ballpark we were searching in. I made the mistake of saying an actual number that was in my head but I didn't know where from and I didn't trust it, that the longest river was something like 1,800 miles long. Despite my unconfidence, we became anchored there. Someone else suggested that the thing to do would be to take a quarter of the circumference of earth (which comes to 6,200 miles) as a baseline and adjust for the fact that rivers wiggle. I thought, that's crazy, you must be the mole. I think I answered 1500 miles.
In reality, the longest river is 4,100 miles, the third longest is 3900 miles, and the mole decided that 1800 was dumb and he didn't need to do anything to sabotage us. (I don't remember what the circumference-over-four person submitted. I have a recollection that he was closer than I was, but I also had a recollection that circumference-over-four was actually pretty close, which it isn't especially.)
The other team did considerably better, getting answers in the 8,000s for a true answer of 8,600.
I'd devised a scoring system, where every player submits their own answer, and non-moles score proportional to $-\left|\log\left({\text{given answer} \over \text{true answer}}\right)\right|$; the mole scores the negative mean of everyone else's score. But after calculating it for a few people, we decided we didn't really care, and we probably wouldn't be playing enough rounds for it to become meaningful.
Those questions weren't so great, because we felt there wasn't much you could do to approach them beyond having some idea of the correct answer. For round two we tried to pick questions more amenable to Fermi estimates: annual U.S. electricity consumption (sourced from Wolfram Alpha), and the number of pennies that could fit inside St. Paul's Cathedral. This round, we gave the correct answers to the moles.
I was on team Cathedral, and again did pretty badly. We started by measuring pennies using notepaper for scale, and calculating packing densities, to work out pennies per cubic metre. (I don't remember the answer, but we got pretty close.) But after that it was just a matter of knowing how large St. Paul's Cathedral was likely to be.
I had been stood outside St. Paul's Cathedral a few weeks back, but mostly facing in the wrong direction while tourists took photos of the group I was with. From that vague recollection I thought maybe it was about a thousand metres square at the base, and four stories so about twelve metres high? (Later I looked at a picture of the Cathedral, and realized that I was probably thinking of the dimensions of the entrance hall.) Someone else, who had actually been inside the cathedral, was giving much higher numbers, especially for the base, and someone else was agreeing with his general ballpark. And the other people weren't saying much, so I figured one of those two had to be the mole, and decided to not update very much in that direction. Those numbers were pretty reasonable, and mine were pretty bad. One of them was the mole (not the one I most suspected); I don't remember what he said his strategy was.
Again, I'm not too sure it was a great question; pennies-per-cubic-metre is a question of geometry rather than estimation, and the interior dimensions of St. Paul's Cathedral don't seem much more Fermi estimable than the river question.
The other team got very close to the answer I'd given the mole. Apparently they actually came up with a number off the top of someone's head that was pretty damn close. Embarassingly, the answer I gave the mole was an order of magnitude too high…. I'd sourced it from Wolfram Alpha ahead of time, but then someone asked me to clarify whether it was total energy usage, or just electricity usage. I looked again to check, and I think I used a different query, saw that it said "electricity usage", and didn't see that the number was different. The answer I actually gave was for energy usage.
The mole on that team reported that it wasn't really helpful to know the correct answer without any intermediate steps. That mechanic might be worth experimenting further, but currently I think it doesn't add much, and it's a mild extra hassle when setting up.
I had fun, and hopefully in future I will put much less trust in my estimates of the dimensions of things, but I wouldn't say the session was a particular success. Not a failure either, just kind of "it happened".
Posted on 16 February 2014
|
Comments
A book sometimes cited on LessWrong as recommended reading is E.T. Jaynes' Probability Theory: The Logic of Science. I intend to write a series of posts reading this book, summarizing the key points, and solving the exercises. (There are no solutions in the book.)
The book has over 750 pages. This will take me a long time, if I finish at all. I'm not committing to finishing. For example, if this turns out not to be a thing worth doing, I hope that I will notice that and stop. I'm also not committing to any particular posting rate while I continue.
Preface
Jaynes starts by telling us the audience of his book: readers with some knowledge of applied math "at the advanced undergraduate level or preferably higher". Prior experience with statistics and probability is unnecessary and might be harmful.
Next we get a brief history of the book. The rules of probability theory have been known for centuries, but in the mid 20th century, these were discovered to be rules for statistical inference in general, unique and inescapable. You cannot violate them without producing absurdity. These discoveries interested Jaynes, and he started giving lectures on them, and eventually they turned into a book.
Jaynes contrasts his system of probability with that of Kolmogorov and de Finetti. Kolmogorov's system looks totally different, but Jaynes finds himself agreeing with it on all technical points, and considers it merely incomplete. De Finetti's system looks similar to Jaynes', but has very little agreement on technical matters. (I don't know what Kolmogorov's and de Finetti's systems actually look like.)
One point is touched on briefly, which I think will become a large theme of the book: infinite set paradoxes. Jaynes claims that these appear to come about because of failure to properly define the objects we're working with. In Jaynes' system, an infinite set can only be specified as a well-behaved limit of finite sets. Sometimes you can arrive at the same set in two different ways, and you can ask questions of it which depend on the limiting process used; but if the limiting process is specified, answers become unique and paradoxes disappear.
PTTLOS is sometimes hailed as a champion of Bayesian statistics over frequentist ones, and indeed we learn Jaynes' view on the dispute. He has always been Bayesian, but previously it was for philosophical reasons. Now he claims that theorems and worked-out examples demonstrate Bayesian superiority independent of philosophy. But he also says that neither is universally applicable, and that both methods fall out as special cases of Jaynes' approach.
Frequentist methods have certain problems; Bayesian methods correct these problems, but can only be applied with a certain amount of knowledge of the problem at hand. The "principle of maximum entropy" provides enough structure to use Bayesian methods when we lack knowledge.
Jaynes claims that probability theory also models certain aspects of human reasoning. Someone who tells the truth, and whose listeners are reasoning consistently, but who is not believed. A policy debate where discussion of the issues causes society to polarize into two camps with no middle ground, rather than to bring about a consensus as might naively be expected.
The work is not intended to be merely abstract, and Jaynes gives an example of practical applications in safety concerns. We might discover that a substance is harmful at certain doses, and it might be natural to assume a linear response curve: half the dose is half as harmful. But knowing a little about biology tells us that this will be untrue in many cases; there will be a threshold level, below which the substance is eliminated as fast as it enters the body and causes no ill effects. Using a model which ignores the possibility of threshold levels can lead to false conclusions, however good our data is.
Finally in the preface, we are told the style of presentation of the work. Most chapters in part 1 start with verbal discussion of the nature of a problem, before getting into the math (which Jaynes considers the easy part, for many students). Part 2 is more advanced, and chapters open directly with math. Jaynes places an emphasis on intuitive understanding over (but not replacing) mathematical rigor.
Chapter 1: Plausible Reasoning
1.1. Deductive and plausible reasoning.
Suppose a policeman hears a burglar alarm, sees a broken shop window, and a man in a mask climbing out of that window with a bag of jewelry. The policeman will decide that the masked man is dishonest. But this cannot come from purely deductive reasoning: it may be that the man is the owner, on his way home from a masquerade party, and that someone else broke the window and he is merely protecting his own property.
Deductive reasoning follows from two familiar syllogisms: "A implies B; A; therefore B" and "A implies B; not-B; therefore not-A". We often don't have the necessary information to apply these.
There are two weaker syllogisms which we use in inferential reasoning: "A implies B; B is true; therefore A becomes more plausible", and symmetrically, "A implies B; A is false; therefore B becomes less plausible".
(These are related to fallacies of deductive reasoning which say: "A implies B; B; therefore A" and "A implies B; not-A; therefore not-B". But deductive reasoning has only the states "certain", "impossible" and "unknown". Inferential reasoning is more subtle, and lets us say "A becomes more plausible" without saying "A becomes certain".)
The word "implies" is meant to indicate logical consequences, not physical ones. We might say: "if it will start to rain by 10 AM at the latest, then the sky will become cloudy before 10 AM". The rain at 10 AM can hardly be the cause of the clouds before 10 AM. Clouds cause rain, but uncertainly so, so we cannot say "clouds imply rain". "Rain implies clouds" is a true logical connection, but not (directly) a causal one.
And there is a still weaker syllogism which the policeman uses: "if A is true, then B becomes more plausible; B is true; therefore A becomes more plausible". Concretely, "if a man is a burglar, then it becomes more likely that he will wear a mask and climb out of a broken window carrying a bag of jewelry. He is wearing a mask and climbing out of a broken window carrying a bag of jewelry; therefore it becomes more likely that he is a burglar." The syllogism may seem weak abstractly, but we accept that the man is almost certainly a burglar.
(Jaynes does not here mention the natural sixth syllogism: "if A is true, then B becomes more plausible; A is false; therefore B becomes less plausible". But of course this is true too.)
Deductive reasoning is nice, because it never loses strength. An arbitrarily long chain of deductive inferences, if our premises are certain, will produce a certain result. Inferential reasoning does not permit this, but we will still be able to approach near-certainty in many cases, such as with the policeman and the probably-burglar.
1.2. Analogies with physical theories
Jaynes analogizes our study of common sense to that of physics. It's too complicated to learn everything all at once, but sometimes we produce a mathematical model that reproduces some features of our observations, and we consider this progress. We expect our models to be replaced by more complete ones in future. We don't expect that the most familiar aspects of mental activity will be the easiest to model.
1.3. The thinking computer
In principle, a machine can do anything that a human brain can do. Proof by existence: the human brain does it. If we don't know how to make a machine do something, it's because we don't know how to describe the thing in sufficient detail. This is also true of "thinking".
But as we study common sense, we're going to start to learn about thinking in more detail than we currently have. Whenever we make a mathematical model of some aspect of common sense, we can write a computer program to apply this model.
If we have two very different hypotheses, unaided common sense might be enough to choose one over the other. If we have a hundred similar ones, we need a computer, and we need to know how to program it. Our goal is to develop the theory that lets us program it correctly to solve such problems, in as much depth and generality as we can manage.
Talking about machines is also useful for keeping ourselves focused. The reasoning process actually used by human brains is complicated and obscure, and hard to talk about without becoming side tracked. But we're not trying to explain or emulate a human brain. We're speaking normatively, not descriptively.
Up until now we've been asking how to build a mathematical model of human common sense. A better question would be: how can we make a machine carry out plausible reasoning, following clear principles that express an idealized common sense?
1.4. Introducing the robot
To keep our attention focused, we're going to invent an imaginary robot. We design its brain as we see fit, and we see fit to make it reason according to definite rules. We choose the rules according to desiderata that seem like they would be desirable in human brains: if a rational person discovered that they were violating one of these desiberata, they would wish to revise their thinking.
Our robot reasons about propositions, and for now we restrict it to unambiguous true-or-false propositions. We don't require their truth or falsehood to be easy, or even possible, to establish with certainty, but it must be clear what truth and falsehood actually mean. For example, Jaynes considers both of these propositions to be true:
$$\begin{aligned}
A ≡ & \text{Beethoven and Berlioz never met.}\\
B ≡ & \text{Beethoven's music has a better sustained quality than that of}\\
& \text{Berlioz, although Berlioz at his best is the equal of anybody.}
\end{aligned}$$
Our robot can think about proposition $A$, although its truth or falsehood probably can't be established today. But for now, $B$ is off-limits. Later we'll see whether this restriction can be relaxed, and our robot can help with propositions like $B$. ("See chapter 18 on the $A_p$ distribution.")
1.5. Boolean algebra
At this point Jaynes briefly introduces Boolean algebra. I assume the reader is familiar with it, but I note that we denote conjunction (logical AND) by $AB$, disjunction (logical OR) by $A+B$, and denial (logical NOT) by $\bar A$. $≡$ means "equals by definition".
Also, a brief reminder of certain identities:
- Idempotence:
$AA = A+A = A$.
- Commutativity:
$AB = BA$; $A+B = B+A$.
- Associativity:
$A(BC) = (AB)C = ABC$; $A+(B+C) = (A+B)+C = A+B+C$.
- Distributivity:
$A(B+C) = AB + AC$; $A + (BC) = (A+B)(A+C)$.
- Duality:
$\overline{AB} = \bar A + \bar B$; $\overline{A+B} = \bar A \bar B$.
If $A=B$, by which we mean that $A$ and $B$ are logically equivalent, then $A$ and $B$ must also be equally plausible. This seems obvious, but Jaynes notes that Boole himself got it wrong.
As usual, $A ⇒ B$ means "$A$ implies $B$", i.e. $A+\bar B$. Remember that this is a much narrower statement than it would be in ordinary language; it doesn't mean that there is any actual connection between $A$ and $B$.
1.6. Adequate sets of operations
We have four operations (AND, OR, NOT and IMPLIES) that we can apply to propositions. We can use these to generate many new propositions, but two questions occur to us. Firstly, are there propositions defined from $A$ and $B$ that we can't represent using these operations? Secondly, can we reduce the number of operations without losing any propositions that we can currently generate?
We answer the first question no: any logical function on $n$ variables (of which there are $2^{2^n}$) can be written as a disjunction of conjunctions of arguments and their negations. Each conjunction includes every argument precisely once, either purely or negated, and is true at precisely one point of its domain. For example, $AB\bar C + \bar A \bar B C + \bar A B \bar C$. There is one semi-exception, where we have zero conjunctions (the function which is constantly false), and this can be written $A\bar A$.
We answer the second question yes: it is clear from the previous answer that IMPLIES is unnecessary, and from duality that we can do away with either (but not both) of AND and OR. We can't reduce either of the sets (AND, NOT) or (OR, NOT), but there are two operators which suffice by themselves: NAND, $A↑B = \overline{AB}$, and NOR, $A↓B = \overline{A+B}$.
1.7. The basic desiderata
We now move on to our extension of logic. This will follow from the conditions to be discussed in this section. We don't call them "axioms" because we're not asserting that they're true, just that they appear to be desirable goals. In chapter 2 we'll discuss whether the goals are contradictory, and whether they determine any unique extension of logic.
Our robot must assign a degree of plausibility to each proposition that it thinks about, based on the evidence it has available. When it collects new evidence, it must update these degrees of plausibility. To store these plausibility assignments in the brain, they have to be associated with some physical quantity, such as a voltage level. This means there must be some kind of association between degrees of plausibility and real numbers. Thus we have
- Desideratum (I). Degrees of plausibility are represented by real numbers.
This is motivated by physical necessity, but appendix (A) shows that it's also a theoretical necessity.
Being more specific, two other properties of this representation will be useful. Firstly, that a greater degree of plausibility is represented by a greater real number. And secondly, continuity; this is difficult to state precisely yet, so we say it intuitively: an infinitesimally greater plausibility should correspond to an infinitesimally greater number.
The plausibility assigned to a proposition will often depend on whether some other proposition is true. We use the symbol $A|B$ to denote "the conditional plausibility that $A$ is true, given that $B$ is true", or "$A$ given $B$". We also have, for example, $A | BC$, the plausibility of $A$ given that $B$ and $C$ are true; and $A+B \mid CD$, the plausibility that at least one of $A$ and $B$ is true, give that both of $C$ and $D$ are true; and so on.
(I mildly dislike this notation, myself, but we're stuck with it. I think the problem is spacing: the way it's usually typeset, $A + B | CD$ looks like it should be parethesised $A + (B|(CD))$ rather than $(A+B)|(CD)$. I prefer to have more whitespace around operators with low precedence.)
We're not going to attempt to define constructions like $A|B$ when $B$ is impossible; for example, if we write $A|BC$, we are implicitly assuming that $B$ and $C$ are compatible.
We want our robot to think in a way which is qualitatively like the way humans try to reason, as described by the above weak syllogisms and similar ones. So suppose the robot has prior information $C$ which gets updated to $C'$ such that the plausibility for $A$ is increased, but the plausibility of $B$ given $A$ does not change:
$$ A|C' > A | C; \\
B|AC = B|AC'. $$
This can never decrease the plausibility that both $A$ and $B$ are true:
This doesn't say anything about how much the plausibilities change, but it gives a sense of direction. These qualitative requirements will be stated explicitly in chapter 2; for now we sum them up as
- Desideratum (II). Qualitative correspondance with common sense.
Finally, we wish our robot to reason consistently. By this we mean
- Desideratum (IIIa). If a conclusion can be reasoned out in more than one way, then every possible way must lead to the same result.
- Desideratum (IIIb). The robot always takes into account all of the evidence it has relevant to a question. It does not arbitrarily ignore some of the inormation, basing its conclusions only on what remains. In other words, the robot is completely nonideological.
- Desideratum (IIIc). The robot always represents equivalent states of knowledge by equivalent plausibility assignments. That is, if in two problems the robot's state of knowledge is the same (except perhaps for the labeling of the propositions), then it must assign the same plausibilities in both.
Desiderata (I), (II) and (IIIa) are structural requirements on the robot's brain, while (IIIb) and (IIIc) show how the robot should relate to the outside world.
It turns out that these are all the desiderata we need. There is only one set of mathematical operations for manipulating plausibilities which satisfies all of them; they uniquely determine the rules by which our robot must reason. These rules will be deduced in chapter 2.
Our robot's mental state about any proposition is going to be represented by a real number. A human's mental state is much more complicated: we judge propositions as being plausible, desirable, amusing, etc. A human's mental state might be better represented as a many-dimensioned vector of real numbers.
Unemotional propositions like "the refractive index of water is less than 1.3" can be represented with fewer dimensions than propositions like "your mother-in-law just wrecked your new car". The situations we encounter in real life are often the ones requiring many coordinates. This may help explain why human reasoning about such situations is hard to model; and why math and science (dealing with propositions that generate simple mental states) are so successful.
Many of these coordinates are not useful to us. We don't want our robot to get bored with a lengthy problem, or to get confused by emotional factors. But there is a large unexplored area of possible generalizations of the theory that we'll be developing, which could more accurately model actual human brains.
Ordinary language, if used carefully, does not need to be less precise than formal logic. But it's more complicated, giving it richer possibilities of expression. In particular, it has many ways to imply something without saying it, which are lost on formal logic. The claim "I believe what I see" and the retort "he doesn't see what he doesn't believe" would have the same meaning in formal logic, but convey opposite meanings in common language.
Another example is that the word "is" is not commutative in common language. This example is taken from a math textbook: consider a straight line in the plane, and an infinite set of points in the plane, and the projections of the points onto the line. Then the statements
- The projection of the limit is the limit of the projections
- The limit of the projections is the projection of the limit
Are not considered equivalent. The projections may have a limit while the points themselves do not (but not vice versa). The first statement implicitly asserts that the points have a limit, and is true conditional on that premise; the second implicitly asserts only that the projections have a limit, and is false.
We can also distinguish between two different senses of the word "is". The epistemological sense, "the room is noisy", expresses something about the speaker's perception. The ontological sense, "there is noise in the room", asserts the physical existence of something. Mistaking one's thoughts and sensations for external realities is called the "mind projection fallacy", and causes much trouble in probability theory and elsewhere.
(This is Jaynes' way of reminding us that the map is not the territory. It is not meant to imply that one's thoughts and sensations are completely unrelated to the real world.)
We will not attempt to make our robot grasp common language.
1.8.2. Nitpicking
Sometimes people question the second strong syllogism, "A implies B; not-B; therefore not-A". But Jaynes is happy to use it, noting among other things that if we exhibit a counterexample to a supposed theorem, then the supposed theorem is considered disproved. A new logic might lead to results which Aristotelian logic can't talk about, and that's just what we're trying to create here. But if a new logic was found to disagree with Aristotelian logic, then we would consider that a fatal flaw in the new logic.
There are attempts to develop multiple-value logics. But arguments presented in appendix A suggest that there is no new content in these. An $n$-valued logic applied to a set of propositions is equivalent to a two-valued logic applied to a larger set; or it is inconsistent.
Posted on 02 February 2014
|
Comments
There's a fairly well-known (as these things go) IOCCC entry ("westly.c") to calculate pi. It looks like this:
#define _ F-->00 || F-OO--;
long F=00,OO=00;
main(){F_OO();printf("%1.3f\n", 4.*-F/OO/OO);}F_OO()
{
_-_-_-_
_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_
_-_-_-_
}
This prints 3.141, but you could get more digits by increasing the size of the circle (and changing the printf call).
I recently decided to port this to python. Here's the result:
class F:pass
s=F();_=F();
a=[];3;d=[];
A=(lambda:a.
append(1) or
s);D=(lambda
:d.append(1)
or s);l=len;
_.__neg__=(#
(lambda: _))
_.__sub__=(#
lambda x: (D
() and A()))
s. __sub__=\
lambda x:A()
-_
_-_-_-_
_-_-_-_-_-_
-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_
-_-_-_-_-_-_-_-_-_-_
-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
-_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_-_-_-_-_
-_-_-_-_-_-_-_-_-_-_-_
-_-_-_-_-_-_-_-_-_-_
_-_-_-_-_-_-_-_-_
-_-_-_-_-_-_-_
_-_-_-_-_-_
_-_-_-_
-_
print"%.3f"%(8.*l(a+d)/l(d)**2)
The rest of this post is spoilers, so stop reading if you'd like to figure out what's going on for yourself.
How it works
The original C version works by counting the area of the circle in variable F, and its diameter in variable OO. Then it calculates $ π = {4A \over d^2} $, and prints this to 3 decimal places.
In more detail, _ is #defined to the statement F-->00 || F-OO--;. Since F is never positive in this program, by default this decrements both F and OO. But _ mostly appears in the context of -_, which becomes -F-->00 || F-OO--;, which will only decrement F (since F is negative whenever this statement occurs).
So the diameter of the ascii circle is counted as the number of lines, and its area is counted as the total number of _s it contains.
The python version uses a similar algorithm, but implemented differently. There's no preprocessor, so instead I use operator overloading. _ is a variable. Strings like _-_-_ count the total number of _s minus one into variable a, and count one into variable d. Then we use $ π = {8(a+d) \over d^2} $. 8 because it's only a semicircle, and $(a+d)$ because a is missing one _ per line.
How it does that is easy enough. _ has a __sub__ method which increments both a and d, and returns a new variable, s. s has a __sub__ method which just increments a and returns s. So a line like _-_-_-_ becomes s-_-_ becomes s-_ becomes s, and on the way it counts 1 into d and 3 into a.
We can also start a line with a -. -_ is defined to just return _, so it doesn't change anything. The top and bottom lines, -_, are just there for aesthetic reasons, they don't do anything at all.
As an implementation detail, a and d are actually lists. You can't call a += 1 in a python lambda, because python's lambdas are crippled (limited to a single expression, whereas a+=1 is a statement). So I have functions
A = lambda: a.append(1) or s
D = lambda: d.append(1) or s
which are slightly shorter, easier to lay out, and I think more in the spirit of the thing, than writing def A(): global a; a+=1; return s. (There's also some historical motivation. I originally used I = lambda x:x.append(1) or s and called I(a) and I(d). But I had difficulty fitting it into the square block, and in the course of experimentation ended up with what I have now. I could have gone with a and d as one-element arrays and def I(x): x[0]+=1; return s. But, whatever.)
Then in the final line, l(a+d) is just len(a+d), and summing arrays concatenates them so that's the same as len(a)+len(d). And l(d) is just len(d).
Here's an unobfuscated version of the header:
class F:pass
s = F()
_ = F()
a = []
d = []
A = lambda: a.append(1) or s
D = lambda: d.append(1) or s
l=len
_.__neg__ = lambda: _
_.__sub__ = lambda x: D() and A()
s.__sub__ = lambda x: A()
Incidentally, I only have one code block, class F:pass. When I decided to lay the header out in a rectangle, because yay geometric shapes, that line forced the width because I can't put anything before or after it. I wanted to go with F = type('', (), {}). But for some reason, that makes subtraction throw a TypeError:
>>> class F: pass
...
>>> x = F()
>>> x.__sub__ = lambda x: 3
>>> x-x
3
>>> G=type('',(),{})
>>> y = G()
>>> y.__sub__ = lambda x: 3
>>> y - y
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
TypeError: unsupported operand type(s) for -: '' and ''
I don't know why that happens.
You might be wondering, if I'm using the same algorithm as the C version, why is my semicircle so much larger than the original circle? That's an annoying quirk of mathematics.
With a circle, we have $ π = { 4a \over d^2 } $. For fixed $d$, we need an area $ a = { πd^2 \over 4 } $. But our area is an integer. So for fixed $d$, we can get an upper and lower bound on $π$, and we choose to display one of these. As we increase $d$, the bounds get tighter, but the lower bound doesn't move monotonically up, and the upper bound doesn't move monotonically down. $ d=16 $ is the first time that either bound gives us three decimal places, with an area of 201.
I had to go with a semicircle, because of significant whitespace, so I instead need an area $ a = { πd^2 \over 8 } $. With a diameter of 16, I could choose between an area of 100 or 101. These give π as 3.125 or 3.15625, which aren't even correct to two decimal places. If I wanted three decimal places, I needed a diameter of 32 and an area of 402. (My semicircle is actually 34 lines tall, but as noted above, the first and last lines don't do anything.)
Pedants will note that π rounded to three decimal places should actually be 3.142. I could have acheived that with a diameter of 34 and an area of 454. With a full circle, we could go for diameter 17 and area 227.
Posted on 18 January 2014
|
Comments
It feels like most people have a moral intuition along the lines of "you should let people do what they want, unless they're hurting other people". We follow this guideline, and we expect other people to follow it. I'll call this the permissiveness principle, that behaviour should be permitted by default. When someone violates the permissiveness principle, we might call them a fascist, someone who exercises control for the sake of control.
And there's another moral intuition, the harm-minimising principle: "you should not hurt other people unless you have a good reason". When someone violates harm-minimisation, we might call them a rake, someone who acts purely for their own pleasure without regard for others.
But sometimes people disagree about what counts as "hurting other people". Maybe one group of people believes that tic-tacs are sentient, and that eating them constitutes harm; and another group believes that tic-tacs are not sentient, so eating them does not hurt anyone.
What should happen here is that people try to work out exactly what it is they disagree about and why. What actually happens is that people appeal to permissiveness.
Of course, by the permissiveness principle, people should be allowed to believe what they want, because holding a belief is harmless as long as you don't act on it. So we say something like "I have no problem with people being morally opposed to eating tic-tacs, but they shouldn't impose their beliefs on the rest of us."
Except that by the harm-minimising principle, those people probably should impose their beliefs on the rest of us. Forbidding you to eat tic-tacs doesn't hurt you much, and it saves the tic-tacs a lot of grief.
It's not that they disagree with the permissiveness principle, they just think it doesn't apply. So appealing to the permissiveness principle isn't going to help much.
I think the problem (or at least part of it) is, depending how you look at it, either double standards or not-double-enough standards.
I apply the permissiveness principle "unless they're hurting other people", which really means "unless I think they're hurting other people". I want you to apply the permissiveness principle "unless they're hurting other people", which still means "unless I think they're hurting other people".
Meanwhile, you apply the permissiveness principle unless you think someone is hurting other people; and you want me to apply it unless you think they're hurting other people.
So when we disagree about whether or not something is hurting other people, I think you're a fascist because you're failing to apply the permissiveness principle; and you think I'm a rake because I'm failing to apply the harm-minimisation principle; or vice-versa. Neither of these things is true, of course.
It gets worse, because once I've decided that you're a fascist, I think the reason we're arguing is that you're a fascist. If you would only stop being a fascist, we could get along fine. You can go on thinking tic-tacs are sentient, you just need to stop being a fascist.
But you're not a fascist. The real reason we're arguing is that you think tic-tacs are sentient. You're acting exactly as you should do if tic-tacs were sentient, but they're not. I need to stop treating you like a fascist, and start trying to convince you that tic-tacs are not sentient.
And, symmetrically, you've decided I'm a rake, which isn't true, and you've decided that that's why we're arguing, which isn't true; we're arguing because I think tic-tacs aren't sentient. You need to stop treating me like a rake, and start trying to convince me that tic-tacs are sentient.
I don't expect either of us to actually convince the other, very often. If it was that easy, someone would probably have already done it. But at least I'd like us both to acknowledge that our opponent is neither a fascist nor a rake, they just believe something that isn't true.
Posted on 04 January 2014
|
Comments
If you hang out on /r/scifi for long enough, you'll hear someone say that Star Wars is not science fiction. It's fantasy in space, or space opera, or whatever, but it isn't science fiction.
(The example that inspired this post, nine months ago, was this thread.)
And, well, they're wrong.
I want to call it a "no true Scotsman" fallacy. Unfortunately, there's no good definition of science fiction that I can point to and say "whatever Star Wars has or doesn't have, that you think makes it not science fiction, is not part of the definition".
Worse, the person in question usually has a definition of science fiction. (In this case, "science fiction embraces change".) And indeed, it's a definition that Star Wars does not attain.
But what this should tell us is not "Star Wars is not science fiction". It's "your definition of science fiction is broken". Consider:
"No Scotsman takes sugar with their porridge!"
"But my uncle Hamish takes sugar with his porridge."
"No, sorry, I was unclear. I define a Scotsman as a person of Scottish citizenship who does not take sugar with their porridge."
It's a bit ridiculous, isn't it?
Star Wars isn't as bad as that, for (at least) two reasons. Since there's no agreed-upon definition of science fiction, choosing your own is more reasonable than choosing your own definition of Scotsman. (Though, I wonder just how well-defined "Scotsman" is. Is the important factor citizenship, birth, personal identity? A mix? Is a "Scotsman" actually necessarily male, with "Scotsperson" being gender neutral? Still, it's better defined than science fiction.)
The other reason is that the proposed definition of "Scotsman" is a silly definition even to consider. Why are you talking about the conjunction of "Scottish citizenship" and "doesn't take sugar with their porridge"? Is there anything you can say about "people of Scottish citizenship who do not take sugar with their porridge", that doesn't follow trivially from what you know of "people of Scottish citizenship" and "people who take sugar with their porridge"? Whereas the proposed definition of science fiction is often quite a reasonable definition of something that we might want to talk about.
Just not a reasonable definition of science fiction: it doesn't include Star Wars.
I don't think that it's bad, in general, to take a poorly-defined concept and attempt to give it a rigorous definition. And sometimes we might find that in doing so, there are some things that we've been thinking of as frantles that don't seem to fit in very well with all the other things that we think of as frantles, and maybe we should stop calling them frantles. I think something like that happened with the question of whether or not 1 is a prime number, for example.
But I think that if you do that to science fiction, and eliminate Star Wars, you've done something wrong.
My reasoning for this is basically "Star Wars is obviously science fiction, duh". But a more compelling argument is: if you eliminate Star Wars, you're bound to be eliminating a whole load of other stuff. For example, if the Force disqualifies Star Wars for being too magical, then presumably Stranger in a Strange Land doesn't count either. It's been a while since I read the 2001 series, but I think David Bowman would disqualify those as well.
There are stories that I consider science fiction that I wouldn't make this complaint about. If someone's definition excluded Ted Chiang's 99 Letters, that would be fine. But when you say that Star Wars isn't science fiction, you're no longer speaking the same language as your audience, unless your audience is composed mostly of the sort of people who try to come up with rigorous definitions of science fiction.
It's also important to note that whether or not a work counts as science fiction is fundamentally unimportant. If you read a book, and you're not sure whether it counts as science fiction, it's not because you're ignorant about the book. Learning that it is or isn't science fiction won't teach you anything new.
But still. Communicating clearly is important, and if you talk about science fiction and don't intend to include Star Wars, you're failing at that.
Posted on 22 December 2013
|
Comments
Chicken is a well-known two-player game in which the players get inside different cars, drive towards each other, and hope that the other player swerves out of the way. If both players swerve, they both lose small amounts of charisma. If one player swerves and the other doesn't, the swerver loses a slightly larger amount of charisma, and the non-swerver gains a small amount. If neither player swerves, both lose a large (occasionally fatal) amount of HP, and a small amount of charisma.
It is sometimes said[citation needed] that there is an optimal strategy to playing Chicken: after pointing your car at your opponent, remove your steering wheel. Now you can't swerve, so she knows that she can either swerve or crash.
Hearing this strategy, you head down to your local Chicken field, armed with your trusty screwdriver, and eager for a game. You quickly find an opponent. The two of you perform the traditional squaring-off ritual, enter your respective vehicles, and wheel around to face each other. You take your screwdriver in hand, smile sweetly at your opponent… and realise that she has had the same idea, and is already removing her steering wheel.
Are you still going to remove your own wheel? Or are you going to swerve?
It's easy to think that Chicken can turn into a game of "who can precommit first". We race to remove our steering wheels; if I win, then you have to swerve or crash, and if you win, then I have to swerve or crash.
But what if I put on a blindfold? Now if you remove your steering wheel, I won't know about it. What good does it do you then? Even if you always remove your steering wheel, assuming your opponent doesn't remove theirs first - and even if I know that you do that, and you know that I know, and so on - do I know that you're still going to do it when I can't see you do it? You'd like me to think that you will, but how do you convince me? And even if you do convince me, I can still remove my own steering wheel, and if I do it while blindfold I won't know if you beat me to it.
With a blindfold, I'm not precommiting not to swerve, although I can do that as well if I choose. I'm precommiting to ignore your precommitments. (Sort of. I'm precommiting not to receive any sensory input about your precommitments. I can still react to your precommitments, e.g. if both you and my model of you precommit despite me not seeing you do it.)
Of course, you can also put on a blindfold. So maybe we race to do that? But then I can tell you before the game that even if you put on a blindfold, I'm still removing my steering wheel. And you say there's no reason for me to do that, so you don't believe that I will. And I say, "try me". If I've said this in front of a large audience, the cost to me of swerving just went up. Moreso if some of the audience are potential future blindfold opponents.
And you can say the same thing to me. But this meta-level is different. If you've removed your steering wheel, you can't swerve. If you've blindfolded yourself, you can't see me precommit. Those are credible precommitments. There's no object-level reason for me to copy you after you've already done it. But just telling me of your precommitment is far less credible, you can always change your mind.
So if you tell me that you're going to ignore my precommitment to ignore your precommitment, I can tell you the same thing, hoping to change your mind.
Assuming neither of us claims to back down, what happens now? We face off against each other, and if I blindfold myself, I don't know whether you're going to do the same, and I don't know whether you're going to remove your steering wheel, and you know I don't know, and I know you know I don't know… and it seems to me that we're back at the original game.
(Incidentally, I've ignored the possibility that a steering wheel might be replaceable; or that a blindfold can be removed, or light enough to see through from the inside. These possibilities make your precommitments less credible.)
Posted on 07 December 2013
|
Comments
Human brains are bad at evaluating consequences. Sometimes we want to do something, and logically we're pretty sure we won't die or anything, but our lizard hindbrains are screaming at us to flee. Comfort Zone Expansion (CoZE) is an exercise that CFAR teaches to get our lizard hindbrains to accept that what we're doing is actually pretty safe.
Roughly it involves two steps. One: do something that makes our lizard hindbrains get pretty antsy. Two: don't get eaten as a result.
I organised a CoZE exercise for LessWrong London on Septmeber 1st. We had a total of eight participants, I think I was the only one who'd done any structured CoZE before.
My plan was: we meet at 11am, have a discussion about CoZE, play some improv games to warm up, and then head to the nearby mall for 1.30 pm. In reality, the discussion started closer to 12pm, with some people showing up part way through or not until it was finished.
After finishing the discussion, we didn't end up doing any improv games. We also became slightly disorganised; we agreed on a meeting time an hour and a half in the future, but then our group didn't really split up until about twenty minutes after that. I could have handled this better. We got distracted by the need for lunch, which I could have made specific plans for. (Ideally I would have started the discussion after lunch, but shops close early on Sunday.)
Report
My solo activities went considerably less well than I'd expected. My first thing was to ask a vendor in the walkway for some free chocolate, which annoyed her more than I'd expected. Maybe she gets asked that a lot? It was kind of discouraging.
After that I wanted to go into a perfume shop and ask for help with scent, because I don't know anything about it. I wandered past the front a couple of times, deciding to go when the shop was nearly empty, but then when that happened I still chickened out. That, too, was kind of discouraging.
Then I decided to get back in state by doing something that seemed easy: making eye contact with people and smiling. It turns out that "making eye-contact" is a two-player game, and nobody else was playing. After some minutes of that I just gave up for the day.
In my defense: I had a cold that day and was feeling a bit shitty (while wandering near the perfume shop I got a nose-bleed, and had to divert to the bathroom temporarily), and that might have drained my energy. I did also get a few minor victories in. The most notable is that I did some pull-ups on some scaffolding outside, and someone walking past said something encouraging like "awesome". (I'd like to do these more often, but the first time I tried there was ick on the scaffolding. There wasn't this time, so I should collect more data.)
[[I spoke with Critch from CFAR a few days afterwards, and he gave me a new perspective: if I go in expecting people to respond well to me, then when they don't, that's going to bother me. If I go in expecting to annoy people, but remembering that annoying people, while bad, doesn't correspond to any serious consequences, then it's going to be easier to handle. For any given interaction, I should be trying to make it go well, but I should choose the interactions such that they won't all go well. (Analogy: in a game of Go, the stronger player might give a handicap to the weaker player, but once play starts they'll do their best to win.)
He also gave me a potential way to avoid chickening out: if I imagine myself doing something, and then I try to do it and it turns out to be scary, then that feels like new information and a reason to actually not do it. If I imagine myself doing something, being scared and doing it anyway, then when it turns out to be scary, that no longer counts as an excuse. I haven't had a chance to try this yet.]]
Other people had more success. We'd primed ourselves by talking about staring contests a lot previously, so a few people asked strangers for those. I think only one stranger accepted. Trying to get high-fives was also common; one person observed that he sometimes does that anyway, and has a much higher success rate than he did in the mall. One person went into a high-end lingerie store and asked what he could buy on a budget of £20 (answer: nothing). And of course there were several other successes that I've forgotten. I got the impression that most people did better than me.
There was interest in doing this again. At the time I was hesitant but realised that I would probably become less hesitant with time. I've now reached a point where I, too, would quite like to do it again. We haven't got any specific plans yet.
Things to take away:
- Have some well-defined way to transition from "about-to-start" to "started".
- Having an audience makes some things much easier. This is potentially a way to escalate difficulty slowly.
- When I did CoZE at the CFAR workshop I was hanging out with someone, who encouraged me to actually do things as well as provided an audience. At the time I wondered whether the fact that we were together meant I did less, but I did far more with her than by myself.
- We didn't do anything beforehand to get in state, like improv games. I can't say whether this would have helped, but it seems like it might have done.
- We had a nonparticipant volunteer to be a meeting point if participants wanted to finish early. If she hadn't been there, I might not have quit twenty minutes early, but given that I did, it was nice to be able to hang out. This might be a good way to enable longer sessions.
An objection
During the discussion about ethics, someone brought up an objection, which I think cashes out as: there are good places to expand our comfort zones into, there are bad places, and there are lame places. A lot of the stuff on the recommended list of activities is lame (do we really need to be better at asking people for staring contests?), and it's not clear how much it generalises to good stuff. Under the novice-driver line of thought, bothering people is an acceptable cost of CoZE; but if we're using CoZE for lame things, the benefits become small, and maybe it's no longer worth the cost.
I guess this boils down to a question of how much the lame stuff generalises. I'm optimistic; for example, it seems to me that a lot of the lame stuff is going to be overcoming a feeling of "I don't want to bother this person", which is also present in the good stuff, so that particular feature should generalise. (It may also be that the lame stuff is dominated by the good stuff, so there's no reason to ever practice anything lame; but that seems a sufficiently complicated hypothesis to be low prior.)
(There's also a question of whether or not people are actually bothered by strangers asking for staring contests. My initial assumption was not, but after doing the exercise, I'm not sure.)
Posted on 18 November 2013
|
Comments
(Fri, 7 Apr 2017: Importing this post from its original home as a gist.)
I turned my Raspberry Pi into a robot, controlled by a Wii nunchuk. It's surprisingly easy to do - at least, surprisingly to me, who has not previously made a robot. But because it's surprising, it might help others to have a guide, so here one is.
Parts
I'm linking to SKPang for most of these, but Sparkfun and Adafruit would be good places to look if you're in the US.
(If you're in the UK, a word of caution - I bought motors and some other stuff from Sparkfun to save £7 over SKPang, but the package got stopped at customs and I had to pay £4 VAT and £8 handling fees. My understanding is that this will only happen on packages whose contents are worth more than £15, but you'd be a fool to trust me on this. It didn't happen when I spent £20 at Adafruit or £5 at Sparkfun. YMMV.)
-
Raspberry Pi - for the robot logic. An Arduino or similar could be substituted (though the software would need to be rewritten).
-
Wii Nunchuk - if you have a USB gamepad you could use that instead (though again, the software would need to be partially rewritten).
-
SKPang starter kit A - I actually only used the cover, breadboard, and jumper wires from this. (You can buy each of those seperately.) There are probably many similar covers that you could use. SKPang offer two other starter kits, but those have bigger covers. I also stuck a small breadboard on top, which I used, but it wouldn't have been any trouble not to have it.
-
Wire - I mostly cut solid core wire. I also used two jumper wires, but again, if I hadn't had them, that wouldn't have been a problem. They're convenient for prototyping, but they can get in the way.
-
Two each of motors, wheels, and brackets. I used blu-tac to attach them to the case. Note that the motors are sold individually, the wheels and brackets are sold in pairs. I chose 100:1 motors instead of 30:1 to get more power at the expense of speed; having seen the 100:1 in action, I don't think 30:1 would be much good at all in the face of obstacles (but I don't trust myself to make that judgement accurately).
-
Ball caster - for stability. I attached this with blu-tac, as well.
-
Nunchuk adapter. I don't think this comes with header pins (to plug it into the breadboard), so you'll need them as well. Adafruit sells a different one, which does come with a header. Both of these will need soldering.
-
SN754410 Quad half-H bridge. A half-H bridge lets us connect an output to one of two inputs (e.g. power or ground). Two half-H bridges form an H bridge, which lets us run a motor in either direction. Four half-H bridges let us run both motors in either direction, independently.
-
Battery pack - because you don't want a robot tethered to a wall socket. I'm sure there are cheaper solutions, but I already had this for my phone.
-
Tools - you'll need access to wire cutters and a wire stripper (for cutting and stripping the solid core wire); a soldering iron (for the nunchuk adapter, and attaching wires to the motors); and preferably a drill (to make holes for the wires coming from the motors, but they can just run around the outside). If you have a local hackspace, it probably has all these things available for you to use.
Construction
I have a one-page datasheet that tells you which pin is which on both the Pi and the SN754410. The original datasheet for the SN754410 is also fairly readable.
We'll start by getting a single motor to run. Attach a wheel, and solder a length of wire to each of its terminals.

Plug the quad half-H bridge into your breadboard. We'll connect the motor to 1Y and 2Y, and drive it forwards by sending 1Y high and 2Y low, vice-versa for backwards, and sending both low to turn it off. So connect the following pins to power (specifically, to the Pi's 5V header pin):
-
Vcc1, the input voltage. The chip requires this to be between 4.5 and 5.5V.
-
Vcc2, the output voltage. Ideally this would be around 7V, to drive the motors at 6V, but 5V is acceptable, and it's what we have available.
-
1,2EN, so that inputs 1 and 2 are always enabled.
Also connect the four ground pins to ground. (I think the reason there are four is for heat-sinking purposes: if you're sending four 1A output currents, you might not want to send them all through a single wire to ground. With the currents we're actually using, you probably could get away with just connecting one pin to ground.)

Having done that, connect GPIO 7 to 1A and GPIO 0 to 2A. (This is using WiringPi numbers - the Broadcom numbers are 4 and 17 respectively. Obviously other GPIOs will work, but my code assumes 7 and 0.) Connect the motor's terminals to 1Y and 2Y.

Test that it works by running the following commands (you'll need WiringPi:
$ sudo gpio mode 7 out # set up pins
$ sudo gpio mode 0 out
$ sudo gpio write 7 1 # wheel goes forwards
$ sudo gpio write 7 0 # wheel stops
$ sudo gpio write 0 1 # wheel goes backwards
$ sudo gpio write 0 0 # wheel stops again
(Some of you might be thinking: if the SN754410 is a 5V chip, what guarantee is there that the Pi's 3.3V GPIOs can cause it to read a "high" state? Fortunately, the datasheet specifies that anything above 2V is interpreted as high.)
This is meant to be the left motor. If it runs in the wrong direction, which is about 50% likely, just swap its terminals over on the breadboard.
Now do the same to the other motor, using GPIOs 1 and 2 and outputs 3 and 4. You'll also need to connect 3,4EN to 5V.

Test it, and swap wires if necessary:
$ sudo gpio mode 1 out
$ sudo gpio mode 2 out
$ sudo gpio write 1 1 # forwards
$ sudo gpio write 1 0
$ sudo gpio write 2 1 # backwards
$ sudo gpio write 2 0
Now you need to attach the wheels and caster to the underside of the cover. I use blu-tac for this, but a double-sided sticky pad would presumably also work, or you could even drill holes and screw them in place. (I've drilled holes to send the motors' wires through, but not to attach the motors. It's okay to just have the wires wrap around the back.)

The last thing is to connect the nunchuk. Solder a header to the adaptor, and plug it in the breadboard. Wire it up appropriately: 'd' to SDA, 'c' to SCL, '+' to either 5V or 3.3V (3.3V is probably more sensible, since the nunchuk is usually powered by two AA batteries, but I haven't had problems with 5V), and '-' to ground.

Running
The software is fairly simple; you can grab it from github. It depends on wiringpi-python, which I could only install with Python 2.
Note that it probably only works for revision one boards. If you have a revision two, as far as I know the only change you need is in nunchuk.py, changing /dev/i2c-0 to /dev/i2c-1, but I can't test that.
To run it, simply call sudo ./robot.py and start using the nunchuk's analog stick. (It crashes if there's no nunchuk plugged in, or if you disconnect the nunchuk. This is kind of a bug, but also kind of useful for me because I develop by ssh'ing in over ethernet, and pull out the ethernet cable to play. This bug makes it easy to subsequently kill the process.)

Further development
I have a number of ideas for how to take this further:
-
If I had a USB wifi or bluetooth dongle, I could make it remote-controlled from my phone. I'd probably also need a power source lighter than my current battery pack, and some way of attaching it to the robot.
-
An easy change would be to power the motors from a 9V battery instead of from the Pi. 9V is actually a little high; I'd probably get about 7.5 to 8V after passing through the H-bridge, whereas 6V is supposedly optimal. A voltage regulator would be a worthy addition (or just a suitable resistor).
-
With another two motors and four omni wheels, I could make it capable of holonomic drive (movement in any direction without turning).
-
I could add an odometer. I'm not sure what I'd do with the odometer data, but it is a thing I could add.
Posted on 11 October 2012
|
Comments
(Fri, 6 Dec 2013: Importing this post from its original home as a gist.)
The point of this post is an attempt to calculate e to given precision in bash, a challenge given in a job listing that I saw recently. I kind of got nerd sniped. I wrote this as I went along, so there may be inconsistencies.
First attempt
The obvious method to compute e is as the infinite sum of 1/n!, n from 0 to ∞. This converges quickly, but how far do we have to calculate to get the n'th digit of e? We can deal with that later.
We obviously need a factorial function.
fac() {
if [[ $1 -eq 0 ]]; then
echo 1
else
echo $(( $1 * `fac $(($1 - 1))` ))
fi
}
Since we only have integer division, we obviously can't calculate 1/2!. But note that x/a! + y/(a+1)! = (x(a+1) + y)/(a+1)!. We can use this to recursively calculate (sum 1/k! [0 ≤ k ≤ n]) as numer(n)/n!, where numer(0) = 0, numer(k) = k*numer(k-1) + 1.
numer() {
if [[ $1 -eq 0 ]]; then
echo 1
else
echo $(( $1 * `numer $(($1 - 1))` + 1 ))
fi
}
So now we can calculate the partial sums. Since we still only have integer division, we need to multiply them by a power of 10 to get rid of the decimal point.
nthsum() {
echo $(( 10**($1-1) * `numer $1` / `fac $1` ))
}
Note that this fails for n=0 (10**-1 isn't allowed), but we can live with that.
So this kind of works:
$ for i in `seq 1 15`; do nthsum $i; done
2
25
266
2708
27166
271805
2718253
27182787
271828152
2718281801
27182818261
2252447557
-1174490000
104582974
1946803
Up to n=11, we accurately calculate the first (n-3) digits of e. For n=12 and above, we get integer overflows.
It doesn't look like we can go very far with this: the numbers we're working with are simply too large.
Second attempt
If you google "algorithm to calculate a specific digit of e", this paper comes up: http://eprints.utas.edu.au/121/1/Calculation_of_e.pdf. It provides a simple algorithm using (mostly) integer arithmetic, implemented in ALGOL. It's simple enough to translate into bash:
ecalc() {
let n=$1
echo -n 2.
for (( j = n; j >= 2; j-- )); do
coef[j]=1
done
for (( i = 1; i <= n; i++ )); do
let carry=0
for (( j = n; j >= 2; j-- )); do
let temp=coef[j]*10+carry
let carry=temp/j
let coef[j]=temp-carry*j
done
echo -n $carry
done
echo
}
This isn't quite accurate: the original algorithm calculates m such that m! > 10^(n+1), and the loops over j go from m to 2 instead of n to 2. This means the algorithm is inaccurate for small n. (For n ≥ 27, n! > 10^(n+1) so it works out okay; for 22 ≤ n ≤ 26, we have 10^(n-1) < n! < 10^(n+1) and the result is accurate anyway. It seems like the algorithm is unnecessarily conservative, but we might also find that m! > 10^(n-1) is insufficient for larger n.) For large n, we do unnecessary work, but get the correct result.
We can fix both these problems, but this algorithm isn't especially nice anyway. Its time complexity is O(n^2). Can we do better?
Third attempt
(Spoiler alert: this doesn't go so well.)
The same google search also gives this page: http://www.hulver.com/scoop/story/2004/7/22/153549/352 which hints at an algorithm without providing it explicitly. We can adapt our first attempt for this.
Write numer(n) as a_n, so a_0 = 1 and a_n = n * a_(n-1) + 1. This gives 1/0! + 1/1! + … + 1/n! = a_n / n!. We know that e = lim [n→∞] a_n / n!; but more than this, we can show that for any n ≥ 1, a_n / n! < e < (a_n + 1)/n!.
(Proof of this: (a_n+1) / n! = 1/0! + 1/1! + … + 1/n! + 1/n!. This is greater than e if 1/n! > 1/(n+1)! + 1/(n+2)! + …, which holds if 1 > 1/(n+1) (1 + 1/(n+2) (1 + … )). For n ≥ 1, RHS is ≤ 1/2 (1 + 1/3 (1 + … )) which we know is e-2 < 1.)
So if a_n / n! and (a_n + 1) / n! agree up to k decimal places, these must be the first k decimal places of e.
Moreover, we can extract specific decmial places while keeping to integer division: the fractional part of x/y is (x%y)/y, so the first decmal digit is int( (10*(x%y))/y ) or int( (x%y)/(y/10) ) (assuming y%10 = 0), and we can extract further digits by doing the same thing again.
This gives us an algorithm for calculating e to n decimal places, one digit at a time:
ecalc() {
let a=1
let b=1
let d=0
let k=1
let n=$1
while (( d <= n )); do
while (( a/b != (a+1)/b || b%10 != 0 )); do
let a=k*a+1
let b*=k
let k+=1
done
echo -n $(( a / b ))
let d+=1
let a%=b
let b/=10
done
echo
}
Unfortunately, this only works up to three decimal places before we get overflows. The problem is that b only gets a new power of 10 every time k%5 = 0. Unfortunately 24!/10000 overflows, so we only get digits from k=5, 10, 15, 20. (In fact, ecalc 4 is also correct; but this seems to be just coincidence.)
We can delay the inevitable by keeping track of powers of ten explicitly: when we generate a new digit, if b%10 != 0, increment a counter and consider (10^powten * a)/b and (10^powten * (a+1))/b. This gives us a few more digits, but before long 10^powten * a overflows.
So, how to get around this? Why not just implement arbitrary-precision integers in bash?
It sounds crazy, but we don't actually need a complete implementation. The only operations we need are:
- Add one to a bigint.
- Multiply a bigint by an int.
- Divide a bigint by 10.
- Modulo a bigint by 10.
- Integer division of bigints, with small ratio.
- Modulo a bigint by another bigint, also with small ratio.
The latter two can be implemented with subtraction and comparison, so it shouldn't be too hard.
Let's represent a big integer as an array of numbers, each smaller than 2^32. Since bash can represent numbers up to 2^63 - 1, we can raise n up to 2^31 - 1 before overflows become a serious problem. As of 2010, e was only known up to about 2^40 digits, so this is an acceptable limit. But it's admittedly quite arbitrary, and there's no reason to hardcode it.
We'll want some way of taking an array of numbers and turning it into a bigint, if some of its elements are greater than MAXINT or less than 0. I don't think there's a convenient way of passing around arrays in bash, so let's use a register-based approach, and operate destructively on the variable $res. (This is for convenience: $res will be the output variable of other operations, and we expect normalisation to be the last thing they do.)
normalise() {
local i
for (( i = 0; i < ${#res[@]}; i++ )); do
if (( res[i] >= MAXINT )); then
let res[i+1]+=(res[i] / MAXINT)
let res[i]=(res[i] % MAXINT)
elif (( res[i] < 0 && ${#res[@]} > i+1 )); then
let res[i+1]-=1
let res[i]+=MAXINT
fi
done
}
This doesn't handle every case; for example, a term smaller than -MAXINT will break things. But it will be sufficient for our purposes.
With this, addition and subtraction are easy. We only need addition of an int and a bigint, so will call this addi (i for integer) and operate on the variable $op1.
addi() {
res=( ${op1[@]} )
let res[0]+=$1
normalise
}
Subtraction needs to be defined between two bigints, but we only need positive results.
sub() {
local i
res=()
for (( i = 0; i < ${#op1[@]}; i++ )); do
let res[i]=op1[i]-op2[i]
done
normalise
}
Multiplication and division follow similarly. (We only need to divide a bigint by 10, but allowing an arbitrary int is no harder.)
muli() {
local i
res=(${op1[@]})
for (( i = 0; i < ${#res[@]}; i++ )); do
let res[i]*=$1
done
normalise
}
divi() {
local i
res=(${op1[@]})
for (( i = ${#res[@]}-1; i > 0; i-- )); do
let res[i-1]+="MAXINT*(res[i] % $1)"
let res[i]/=$1
done
let res[0]/=$1
normalise
}
(We note that muli might break if the multiplicand is close to 2^32: if two adjacent terms in $res are sufficiently large, normalise might cause overflows. But we're assuming the multiplicand is at most 2^31 - 1, and testing indicates that this works fine.)
For modi, even though the result is a normal integer, we'll return it in $res like a bigint. The other option would be to echo it, but then we'd need to spawn a subshell to use it. (Test this yourself: compare echo 'echo hi' | strace -f bash to echo 'echo $(echo hi)' | strace -f bash. The first doesn't fork at all, because echo is a builtin command; but the second forks a subshell to run echo hi.) Forking isn't cheating, but it seems worth avoiding.
modi() {
local i
let res=0
for (( i = 0; i < ${#op1[@]}; i++ )); do
let res+="${op1[i]}%$1 * (MAXINT%$1)**i"
done
let res%=$1
}
For division and modulo, we need a ≤ operation; we can use its exit code for the return value. (We return 0 (true) if op1 ≤ op2, and 1 (false) otherwise.)
le() {
local i
local len=${#op1[@]}
(( len < ${#op2[@]} )) && len=${#op2[@]}
for (( i = len-1; i >= 0; i-- )); do
if (( op1[i] > op2[i] )); then
return 1
elif (( op1[i] < op2[i] )); then
return 0
fi
done
return 0
}
Finally we can implement division and modulo. We'll just define a mod operator, which can store the division result in a variable $div.
mod() {
local temp=( ${op1[@]} )
let div=0
res=( ${op1[@]} )
until le; do
let div+=1
sub
op1=( ${res[@]} )
done
op1=( ${temp[@]} )
}
So mod stores $op1 % $op2 in $res, and $op1 / $op2 in $div. Since we know $op1 / $op2 will always be less than 10, we could maybe get a slight speed improvement with a binary search, but I really doubt that's going to be a bottleneck.
It would be foolish not to test these. These Haskell functions (entered into GHCI, which only accepts one-line definitions) will help:
let x = 2^32
let splitint n = if n < x then (show n) else (show (n `mod` x)) ++ " " ++ splitint (n `div` x)
let unsplit s = sum $ map (\(a,b) -> b*x^a) $ zip [0..] $ map read $ words s
splitint turns an arbitrary-precision Integer into a string that we can copy into a bash array. unsplit does the opposite, taking a space-separated list of integers and turning them into an arbitrary-precision Integer. (Haskell is good for this because it has arbitrary-precision arithmetic. I originally tried this in Python, and wasted a lot of time trying to track down a bug in my bash code before realising that Python was wrong.) So we choose a few arbitrary large numbers and verify that everything works as expected. (Unsurprisingly, I caught a few bugs when I actually tried this.)
Having implemented bigints to the extent necessary, we can hopefully extract more digits from e. Arithmetic is ugly now, so we'll split off some functions, all using variables $a and $b.
Some things to note:
b_has_power_10 is faster than got_next_digit, and more likely to fail. So we test that first.- To avoid repeating computations,
echo_next_digit and reduce_a_b simply use the results of a mod b calculated in got_next_digit.
got_next_digit() {
op1=( ${a[@]} )
addi 1
op1=( ${res[@]} )
op2=( ${b[@]} )
mod
div1=$div
op1=( ${a[@]} )
mod
(( div1 == div ))
}
echo_next_digit() {
echo -n $div
}
b_has_power_10() {
op1=( ${b[@]} )
modi 10
(( res == 0 ))
}
increase_a_b() {
op1=( ${a[@]} )
muli $1
op1=( ${res[@]} )
addi 1
a=( ${res[@]} )
op1=( ${b[@]} )
muli $1
b=( ${res[@]} )
}
reduce_a_b() {
a=( ${res[@]} )
op1=( ${b[@]} )
divi 10
b=( ${res[@]} )
}
ecalc() {
a=(1)
b=(1)
d=0
k=1
n=$1
while (( d <= n )); do
until b_has_power_10 && got_next_digit; do
increase_a_b $k
let k+=1
done
echo_next_digit
reduce_a_b
let d+=1
done
echo
}
This still seems to act as O(n^2). Which, in hindsight, shouldn't be too surprising: arithmetic is O(log b); b grows as O(k!); and k grows to approximately 4n. (k! needs to have n powers of 5, which means n ≈ k/5 + k/25 + k/125 + … = k/4.) Since there are O(n) arithmetic operations, we should actually find that this is O(n^2 log n) if we look close enough. That's disappointing; and the algorithm is considerably slower than the previous one (7 minutes versus 40 seconds to calculate 100 digits), which is even more disappointing.
But maybe we can still salvage something. (Or maybe we're just doubling down on a sunk cost.) The bottleneck right now is probably the powers of 10 in b. There's an easy way to see this: ask for e up to 20 places. Then take the values of a and b, put them into Haskell, and see just how many digits we'd actually generated at this point.
It turns out to be about 130. (And this only took twelve seconds, so we're beating the second attempt considerably.)
So if we can extract all these digits without needing so many powers of 10 in b, we can do a lot better. We might even be able to beat O(n^2), if k grows slower than O(n). So let's try to do that.
Fourth attempt
We can't simply multiply a by 10 every time we'd like to divide b by 10. That would break the algorithm, for one thing: we'd have to keep track of what power of 10 to multiply a by, and only use it when checking to see if we've got the next digit, not in increase_a_b. (It's okay for b because b only ever gets multiplied, so it doesn't matter whether we do that before or after dividing by 10. But when we do a = k*a + 1, it matters that we haven't already multiplied a by 10.)
That's a minor problem. More severely, our division algorithm was designed for small ratios. If we know a/b < 10, it's okay to examine, a, a-b, a-2b, … to see when we get below b. That won't work so well if a/b could be in the thousands.
Fortunately, we can improve division by using the digits we've already calculated. If we have e = 2.71828… and we haven't reduced a or b at all, then we know a / b = 2.71828…, 10a / b = 27.1828…, 100a / b = 271.828…, etc.
And we know (a-2b)/b = 0.71828, so 10(a-2b)/b = 7.1828…; and (10a - 27b)/b = .1828… so 10(10a - 27b)/b = 10(10(a - 2b) - 7b)/b = 1.828…; and so on.
In short, if we know that a/b = d_0 . d_1 d_2 d_3 … d_n …, then we can extract unknown d_(n+1) by:
let x = a
for i from 0 to n:
x -= d_i * b
x *= 10
d_(n+1) = x/b
These operations are all reasonably fast. (It is, however, O(n), which means we're not going to beat O(n^2).) So, let's try it. We'll store digits of e in an array named e_digits.
next_digit_helper() {
local i
local tmp1=( ${op1[@]} )
local tmp2=( ${op2[@]} )
local x=( ${op1[@]} )
local y=( ${op2[@]} )
for (( i = 0; i < ${#e_digits[@]}; i++ )); do
op1=( ${y[@]} )
muli ${e_digits[$i]}
op1=( ${x[@]} )
op2=( ${res[@]} )
sub
op1=( ${res[@]} )
muli 10
x=( ${res[@]} )
done
op1=( ${x[@]} )
op2=( ${y[@]} )
mod
op1=( ${tmp1[@]} )
op2=( ${tmp2[@]} )
}
got_next_digit() {
op1=( ${a[@]} )
addi 1
op1=( ${res[@]} )
op2=( ${b[@]} )
next_digit_helper
div1=$div
op1=( ${a[@]} )
next_digit_helper
(( div1 == div ))
}
found_digit() {
echo -n $div
e_digits[${#e_digits[@]}]=$div
}
ecalc() {
a=(1)
b=(1)
e_digits=()
d=0
k=1
n=$1
while (( d <= n )); do
until got_next_digit; do
increase_a_b $k
let k+=1
done
found_digit
let d+=1
done
echo
}
Now this works, but it's even slower than the last attempt. We could improve things by reducing a and b as before when possible, but that's not going to gain us much.
There is one other thing we can do, though it seems potentially unsafe. There's a lot of repeated work involved in figuring out how many digits we've accurately calculated. If we guess in advance how high we need to take k, we can save ourselves a lot of work.
Fifth attempt
Recall that we have n digits if a_k/k! and (a_k+1)/k! agree up to n decimal place
s. The difference between these is 1/k!. If k! > 10^(n+1), then the decimal expansion of 1/k! will start with at least n+1 zeros. The only way a_k/k! and (a_k+1)/k! could disagree at or before the nth decimal place is if the digits of a_k/k! in positions n+1, n+2, … log_10(k!) are all 9. If additionally a_k/k! disagrees with e at the nth decimal place, it follows that the digits of e in positions n+1, n+2, …, log_10(k!) are all 0.
e is conjectured to be normal, which would mean that any arbitrarily long string of 0s can be found in its decimal expansion. But the probability of l 0s starting at a given position is 10^-l; so if we ask for, say, 100 digits and take k up to 100, then since log_10(100!) = 157, the probability of getting a digit incorrect is 10^-57, which I feel is acceptable. So let's ignore the problem for now.
extract_many_digits() {
let d=0
op1=( ${a[@]} )
op2=( ${b[@]} )
while (( d <= $1 )); do
mod
echo -n $div
op1=( ${res[@]} )
muli 10
op1=( ${res[@]} )
let d+=1
done
}
ecalc() {
a=(1)
b=(1)
k=1
n=$1
while (( k <= n )); do
increase_a_b $k
let k+=1
done
extract_many_digits $n
echo
}
It's a lot faster, but still slightly slower than the second attempt. (And has the same caveat that as written, it only works for sufficiently large n.)
I've now run out of ideas, which is a bit anticlimactic. (At least, I've run out of ideas that I think will do any good. We could get a more accurate bound on how high to take k; but that could be applied to our second attempt as well. We could reduce a as we go along; but that would make increase_a_b slower, probably gain us very little overall, and certainly not improve on O(n^2).)
So let's return to the second attempt.
Second attempt, take two
Recall that this is the algorithm we're using:
ecalc() {
let n=$1
echo -n 2.
for (( j = n; j >= 2; j-- )); do
coef[j]=1
done
for (( i = 1; i <= n; i++ )); do
let carry=0
for (( j = n; j >= 2; j-- )); do
let temp=coef[j]*10+carry
let carry=temp/j
let coef[j]=temp-carry*j
done
echo -n $carry
done
echo
}
It seems foolish to rely on an algorithm without understanding it, so how does it work? The paper doesn't make it entirely clear, but what's going on is this:
We approximate e as 2 + 1/2! + 1/3! + 1/4! + … + 1/m!, where in our implementation m=n. Rewrite this as 2 + 1/2 (1 + 1/3 (1 + … 1/(n-1) (1 + 1/n) … )).
This in turn is 2 + 1/10 (1/2 (10 + 1/3 (10 + … 1/(n-1) (10 + 1/n (10)) … ))). Some of the 10/k terms are greater than 1; we refactor so that, for example, 1/2 (10 + 1/3 (10 + …)) becomes 1/2 (13 + 1/3 (1 + …)) and then 6 + 1/2 (1 + 1/3 (1 + …)). Eventually we have e = 2 + 1/10 (c + 1/2 (c_2 + 1/3 (c_3 + … 1/(n-1) (c_(n-1) + 1/n (c_n)) … ))) where each c_k < k. It follows that the 1/2 (c_2 + … ) term is less than 1, so c must be 7, the first decimal digit of e.
Rewriting again, e = 2.7 + 1/100 (1/2 (10c_2 + 1/3 (10c_3 + … 1/(n-1) (10c_(n-1) + 1/n (10c_n)) … ))). We apply the same procedure to get the second digit of e, and so on.
The algorithm's coef[j] takes the place of these c_j. To get each digit, we recalculate the c_j in one pass starting from the right; the digit is whatever term is left over outside of the 1/2 (…).
It's worth noting that this algorithm has the same probability of making mistakes as our fifth attempt. So it's probably worth thinking about this probability in more detail.
However, we note that if the calculated sequence of digits ends with d 9s, then only the final d+1 digits have a chance of being incorrect. If they are, then the 9s should all be 0s, and the one preceding them should be one higher. This is reassuring; it permits us to say "if you really can't tolerate the slightest inaccuracy, then ask for more digits than you need, and throw away the final ones as appropriate".
(We could automate the process, but that would require us to guess a new n, then run the algorithm again from scratch. If we want that behaviour, we really ought to write it as a seperate program. In this sense, the fifth attempt was better, because you could store intermediate results and use them to get a head start on later ones.)
I also note that I've spent too much time on this already, and that the implementation as it stands chooses m larger than necessary (except for small n, which we shall soon fix), massively reducing the probability of an error. (For n>50 or so, the probability of an error is smaller than the probability of winning the lottery; if an error does appear, it seems more likely to be from some a mistake somewhere else.) And whatever the actual probability of error is, it was originally small enough that the authors of the paper didn't notice, and after cursory examination I haven't been able to find any instances where the original algorithm made a mistake. (Digit 327 looked promising, being followed by three 0s; but it turned out okay in the end.)
So while I'd like to go into more depth on this issue, I won't do so at this point.
It remains to fix the algorithm for small n. We simply calculate to at least 22 decimal places' worth of precision. This is a little slower than necessary, but the small-n case hardly seems worth optimising.
ecalc() {
let n=$1
let m=n
(( n < 22 )) && m=22
echo -n 2.
for (( j = m; j >= 2; j-- )); do
coef[j]=1
done
for (( i = 1; i <= n; i++ )); do
let carry=0
for (( j = m; j >= 2; j-- )); do
let temp=coef[j]*10+carry
let carry=temp/j
let coef[j]=temp-carry*j
done
echo -n $carry
done
echo
}
We could at this point try to calculate the value of m actually needed. We could even use our arbitrary-precision arithmetic to do it; we haven't implemented logarithms, but we can get an upper bound using the inequality log(sum(a_i * (2^32)^i)) < sum(log(a_i) + i*log(2^32)).
But this would impose O(n^2 log n) startup cost, so is decidedly not a good tradeoff. There may well be better ways to approximate log_10(m!), but again, I've spent too much time on this.
This has been interesting to write, even if more than half of it turns out to be useless.
Posted on 16 June 2012
|
Comments
(Fri, 6 Dec 2013: Importing this post from its original home as a gist.)
The recent post on Hacker News about #! semantics surprised me. I had always assumed that a shebang line like
Would be equivalent to calling
$ /usr/bin/prog -a -b <file>
- but instead, it's
$ /usr/bin/prog '-a -b' <file>
This could only surprise me because I hadn't found out the hard way, so maybe it's not a big deal. Most scripts that I write don't have even a single argument on the shebang line. Most of the rest are Perl scripts, and perl is clever when it comes to parsing a single argument that looks like multiple arguments:
$ echo hi there | perl '-a -n -l -e print $F[0]'
hi
But this behaviour does have consequences, especially with the use of higher-order commands such as sudo, nice and env. For example, the following shebang lines will not work as intended:
#! /usr/bin/sudo -u phil sh
#! /usr/bin/nice -n 19 sh
#! /usr/bin/env perl -n
(Scripts using sudo and nice in a shebang seem unlikely to be distributed, but might find use in site-local maintenance scripts. env can be used to make a script more portable, in case a program isn't in a consistent location across systems.)
So I got to thinking about a program that would act like env for this purpose, but splitting its arguments on whitespace, or even doing full shell-like parsing of quotes.
Of course, such a program already exists: its name is shell. sh accepts the -c option to pass a shell expression on the command line. If this expression comes from a shebang line, word-splitting will be performed just like when typing directly into a shell. As a bonus (arguably), you even get to use things like pipelines, output redirection, shell built-in commands, and forking to the background, all in the shebang line of a script.
There is one downside: normally with a shebang line you can think of the script name and any arguments as being implicitly appended. This no longer holds: sh -c takes an expression, not a program name, and expressions don't take arguments in the same way that programs do. Instead you need to access these arguments through shell variables $0 through $9, $* and $@.
Alas, my first tests failed. It seems that -c requires its argument to be, well, a separate argument, so it's not much use with a shebang. (This is the case when sh is linked to Bash. Perhaps other shells are different, but if it doesn't work in Bash's sh-emulation mode, it probably can't be considered portable.)
So I went ahead and wrote a small script to get this behaviour. I even improved on what I could have done with sh -c: by default the script name and arguments are implicitly appended, but passing -c at the start of the first argument disables this.
I named this script /usr/bin/cmd, so for example the following shebang lines are now possible, and do what you would expect:
#! /usr/bin/cmd sudo -u phil sh
#! /usr/bin/cmd nice -n 19 sh
#! /usr/bin/cmd perl -n
But you can also do things like
#! /usr/bin/cmd grep -v '^#' | perl
to strip comments from the input before you process it. Or perhaps
#! /usr/bin/cmd -c perl "$0" | xargs grep "$@"
to generate a list of filenames in perl and search them for a pattern given on the command line. On a similar note,
#! /usr/bin/cmd -c perl "$0" "$@" | xgraph -nl -m &
might save having a separate file just to pipe the output of a perl script into xgraph.
I have a lisp program which expects an S-expression as input, but I can use
#! /usr/bin/cmd (echo \(&&perl -lne'chomp,print"($_)"'&&echo \)) | sbcl --script
and now it expects plain text. (It could be cleaner, but I wanted to keep it less than 80 characters, and semicolons don't interact well with parentheses and emacs' paredit-mode. This example is probably a little more extreme than is sensible.)
There are also some pitfalls to cmd. If you have a system which does split shebang lines, I think normal behaviour will still work, but anything fancy - any use of -c, or shell processing - will fail. I don't think it would even be possible to port, unless there's some way to tell where the shebang arguments stop and the command-line arguments begin. (You could work this out in most cases by checking which argument names an executable file with cmd on the shebang, but that seems fragile.)
You need to be careful in -c mode to quote properly. Otherwise it will seem to work, but break mysteriously when an argument contains a literal space or wildcard. I think "$0" and "$@" are the constructs you want in almost all cases: everything else I've tried fails, and I haven't found anywhere that these fail. (Perhaps an option to cmd which would cause it to replace % or something with "$0" "$@" would be a good idea.)
If you want to be portable, you also need to worry about the length of your shebang lines. 127 bytes seem to be accepted on all modern systems, but I'll admit that I don't recognise (except perhaps in passing) many of the names in the originally linked article. (But if you want to be portable, you also want to wait until cmd is installed as standard on most systems. This might take a while.)
One pitfall that seems to have been avoided: I was worried that perl (which performs its own parsing of the shebang line) would be too clever for cmd, and recognise switches intended for programs later in a pipeline. This doesn't seem to happen:
#!/usr/bin/cmd -c perl "$0"; echo -l
print "hi";
produces output "hi-l", as intended. But I don't know exactly what rules perl uses, so there may be edge cases.
And I'm sure there are problems that I haven't anticipated. Which is the worst kind of problem.
Ultimately, I'm not sure how much use cmd will be. But until a few days ago, I don't think I'd ever thought about using a shell script in a shebang line, so I guess there's territory yet to explore. I'd be interested in hearing more ideas on the subject.
If you're interested, cmd can be found at http://github.com/ChickenProp/cmd.
Posted on 27 July 2010
|
Comments























































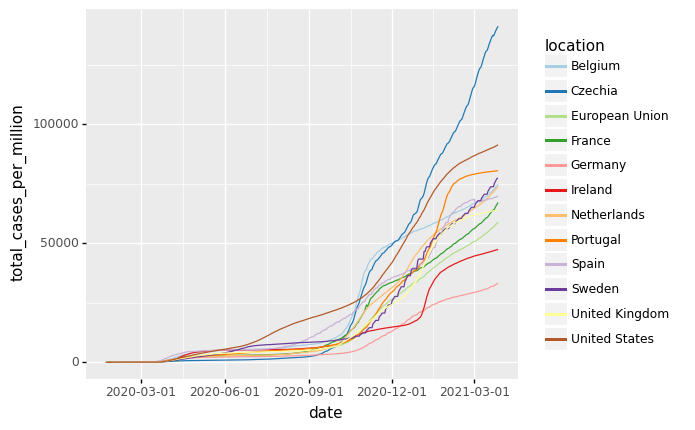
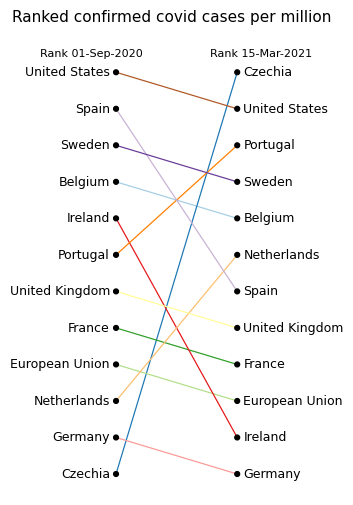











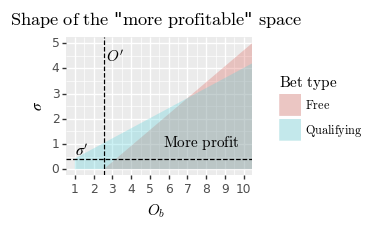
 A photo from a (different) recent LW London meetup
A photo from a (different) recent LW London meetup





